Scout YYF I POJ - 3744（矩阵优化）

Posted 2021-01-05 alingmaomao

题意：一条路上有n个地雷，给出地雷的位置。某人从起点（位置1）出发，走一步的概率是p，走两步的概率是（1-p），然后问有多少概率走过这个雷区。

 

思路：

只要走过最后一个地雷就代表走过雷区了。

而每到 i 这个地方，无非是前一步和前两步走过来的。那么公式就是dp[ i ]= p*dp[ i-1 ]+dp[ i-2]*(1-p)

这是连续没有地雷的区域的走法。那么有地雷呢？

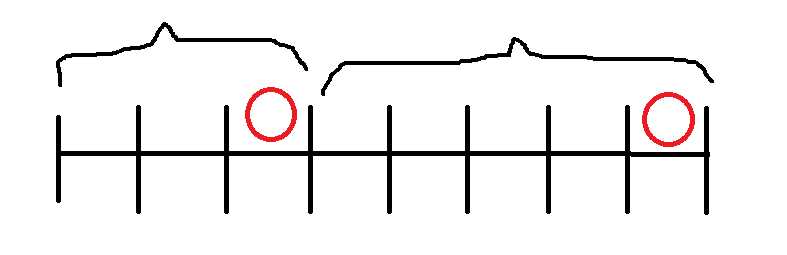
把有红圈的表示地雷。那么像图上进行分段，将上一段不踩雷的概率就可以当做下一段的开始的概率。

则 dp[ a[i] +1] = 1 - d[ a[i] ]; 那么这样就化成求每一段的概率直接相乘就行了。

 

优化： 如果直接乘得话，会超时数据量太大。那么，观察dp[ i ]= p*dp[ i-1 ]+dp[ i-2]*(1-p)， 可以很容易得到这是一个类似 a(n) = p*a(n-1)+ q*a(n-1)

的数列， 那么直接矩阵快速幂就行了。

 

细节：注意，输入的每个地雷的坐标是无序，所以要先对其排序，还有就是，输入了重复的地雷，但是对于幂来说，不需要负数，所以当相同坐标的地雷就不用计算了。

 

ac代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
struct jz
{
    double num[2][2];
    jz operator*(const jz &p)const
    {
        jz ans;
        for (int i = 0; i < 2;++i)
        for (int j = 0; j < 2; ++j)
        {
            ans.num[i][j] = 0;
            for (int k = 0; k < 2; ++k)
                ans.num[i][j] += num[i][k] * p.num[k][j];
        }
        return ans;
    }
};
jz POW(jz x, int n)
{
    jz ans;
    memset(ans.num, 0, sizeof(ans.num));
    for (int i = 0; i < 2; ++i) ans.num[i][i] = 1;
    while (n)
    {
        if (n & 1)ans = ans*x;
        x = x*x;
        n >>= 1;
    }
    return ans;
}
int a[15];
int main()
{
    int n;
    double p;
    jz dp;
    while (scanf("%d%lf", &n, &p)!=EOF)
    {
        dp.num[0][0] = p; dp.num[0][1] = 1.0 - p;
        dp.num[1][0] = 1.0; dp.num[1][1] = 0.0;
        for (int i = 1.0; i <= n; ++i)    scanf("%d", a+i);
        sort(a+1, a + n+1);
        double sum = 1.0;
        for (int i = 1; i <= n; ++i)
        {
            if (a[i] == a[i - 1])continue;
            jz ans = POW(dp, a[i] - a[i - 1] - 1);
            sum *= (1.0 - ans.num[0][0]);
        }
        printf("%.7lf
", sum);
    }
    return 0;
}