5分钟学会红黑树插( insertint elements into a red black tree)
Posted java-learner
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了5分钟学会红黑树插( insertint elements into a red black tree)相关的知识,希望对你有一定的参考价值。
前言:本文解决的问题
- 什么是红黑树
- 什么时候使用红黑树
- 红黑树插入元素时如何保持平衡
1 什么是红黑树
红黑树(Black red Tree) 是一棵自平衡树,每个节点都遵循以下四条:
- 所有节点只能是红色或者黑丝
- 根节点是黑色
- 只存在相邻的红色节点(即红色节点不能有红色的父节点或者红色的孩子)
- 任意从root到Nil节点,经过的路径中黑色节点的数目是一样的。
具体可以见下图

2 什么时候用红黑树
2.1 为什么会提出红黑树
我们知道,一般在平衡二叉树(BST)作插入、删除、更新、查找的时间复杂度是O(log n),但是对于那种变形的BST(往一边偏的,变成线性的)时间复杂度就会变成O(n)。红黑树提供了为插入删除提供了最坏的时间保证2O(log n) ,因为它可以保持自平衡,总能把高度维持在 2log(n+1) (n为节点数目)。
2.1 什么时候用红黑树
相比AVL树而言,红黑树没有严格定义左右子树高度差值,并不严格意义的平衡。如果要涉及到很多插入、删除,用AVL的话会很多次旋转(rotation),此时红黑树是更好的选择。反之,查询多,更改少,即静态的话AVL是更好的选择。在查询效率上,由于AVL树严格平衡,AVL树会比红黑树略快,但时间复杂度是要给数量级上的。此外,相比较AVL树而言,红黑树需要额外的O(n)的空间来存储颜色。
在java集合框架中TreeSet和TreeMap是用红黑树实现的。
3 红黑树的插入
3.1 插入情况分类
放方便后续说明,假设要插入的节点为Z,插入后Z的父节点为,Z.parent;Z父节点的兄弟为Z.uncle
- Case 1插入后Z本身就是根元素

如上图所示,插入后就只有这个一个元素,此时直接把该节点变为黑色即可。
- Case 2 插入后Z的父节点是黑色(Z.parent = black )
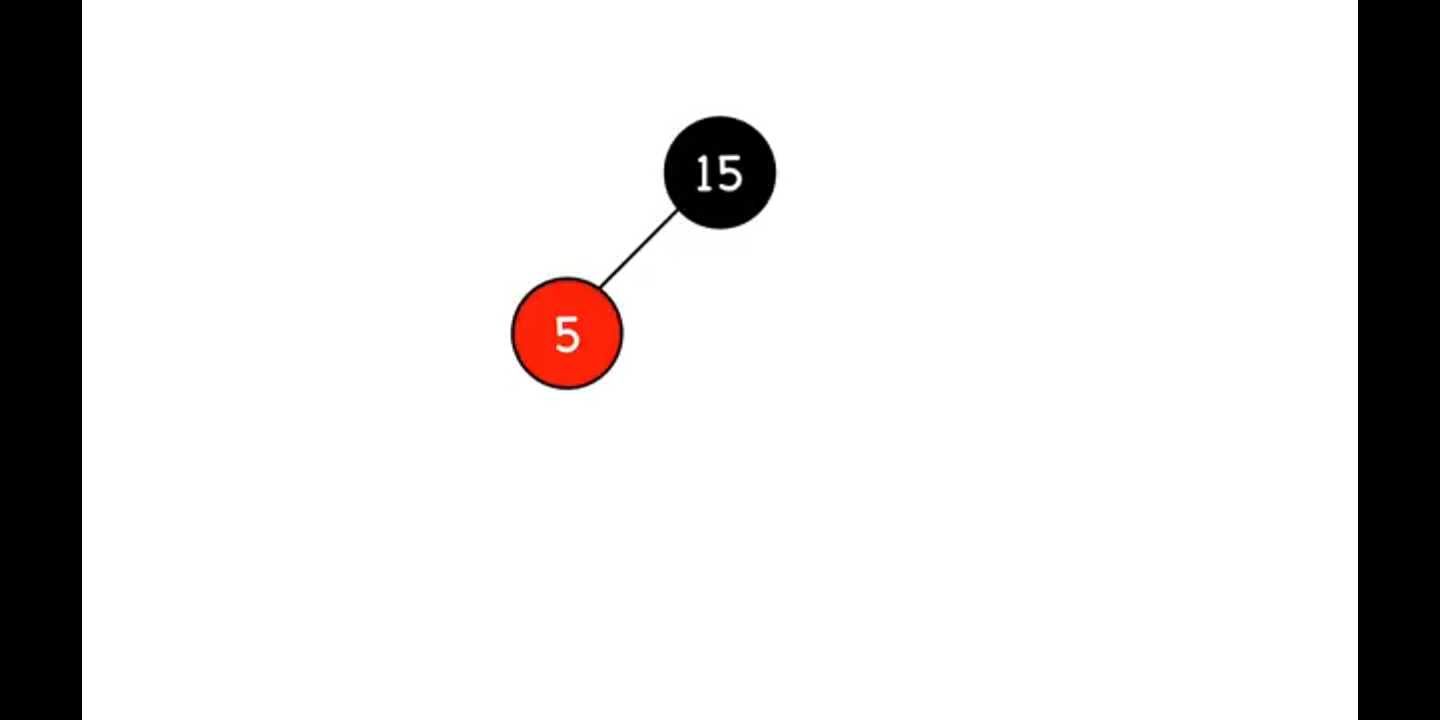
这种完全符合红黑树的特性,不需要做出更改
- Case 3 Z的父节点和叔叔节点都是红色(Z.uncle and parent = red/recolor)
这种违反了红黑树的第三代你特征,即不存在父子节点都是红色的,只需要把父节点和叔叔节点都变成黑色(Z.parent = black; Z.uncle = black),同时上面根节点颜色变成红色。
- Case 4 .Z的父节点是红色,叔叔节点是黑色,Z与父节点和祖父节之间是RL或者LR的情况。(即Z.parent = black and uncle = black(triangle) ->rotate.Z.parent)
和第三种一样违反了父子节点都是红色的特性。此时需要作的是把RL或者LR旋转变成LL或者RR情况的,具体做法就说旋转Z.parent.
Case 5 Z的父节点红色,叔叔节点是黑色的,Z与父节点、祖父节点在一条线上,即LL和RR的情况。(Z.uncle = black(line)->rotate.Z.grandparent &&recolor)
旋转Z的祖父节点,并重新着色,使满足红黑树特性。
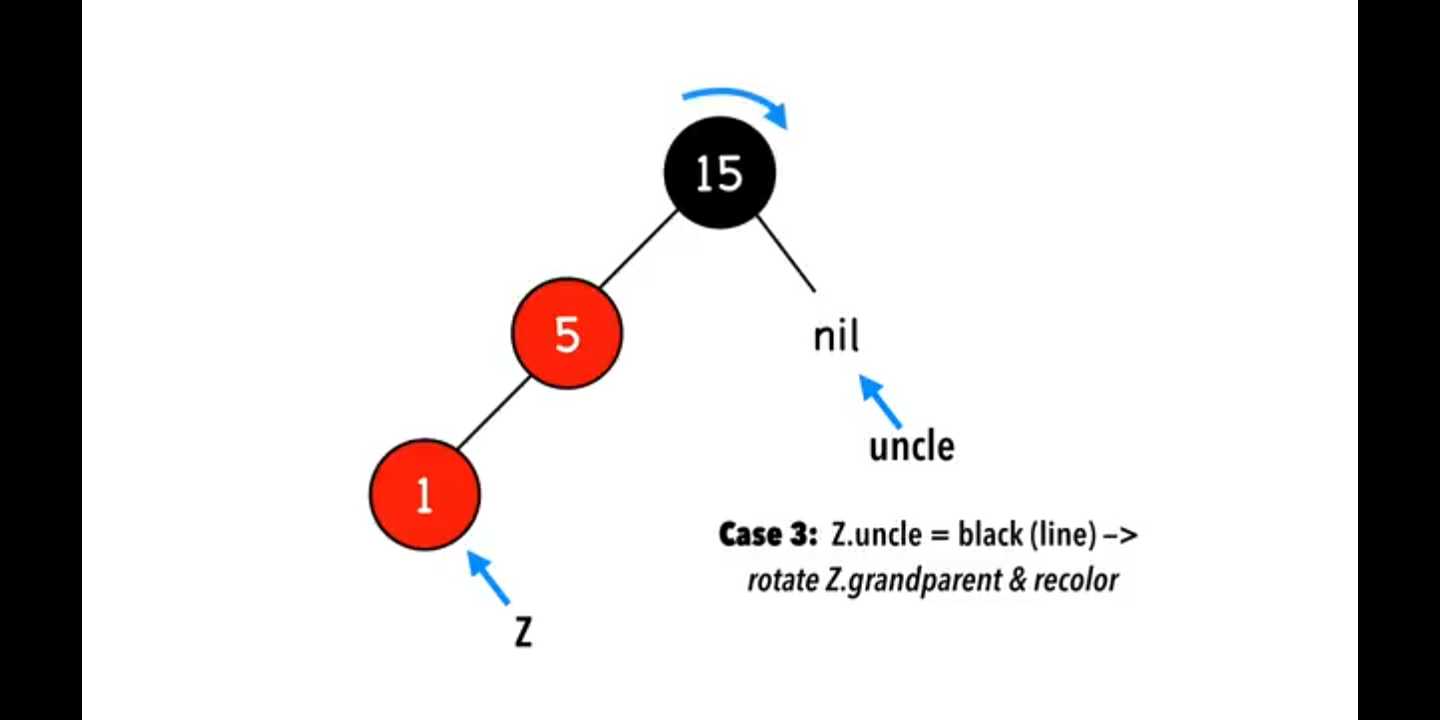
3.2 实际举例(针对case3、case4和case5分别举例)
下图中10是要加入的节点,初始树如下
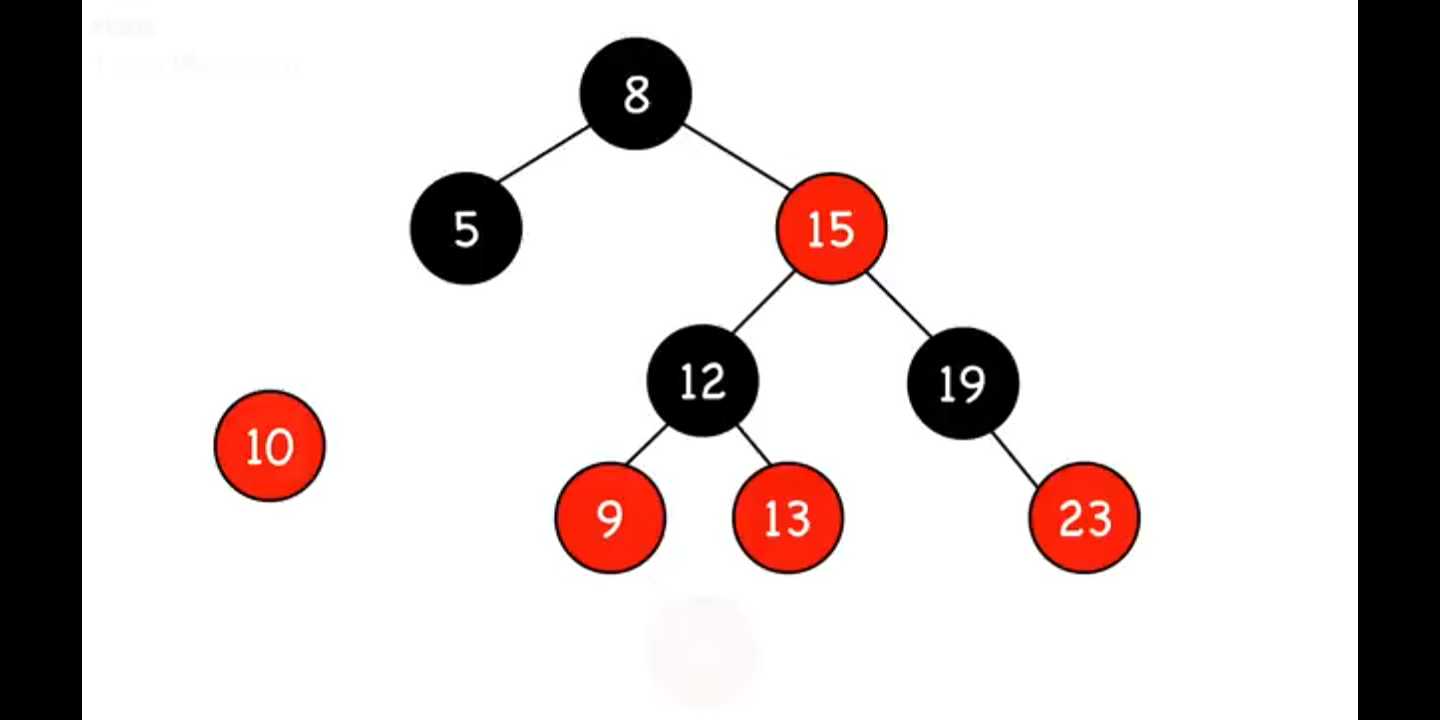
case 3,父亲和叔叔节点都是红色的
把10加在末尾,涂红色
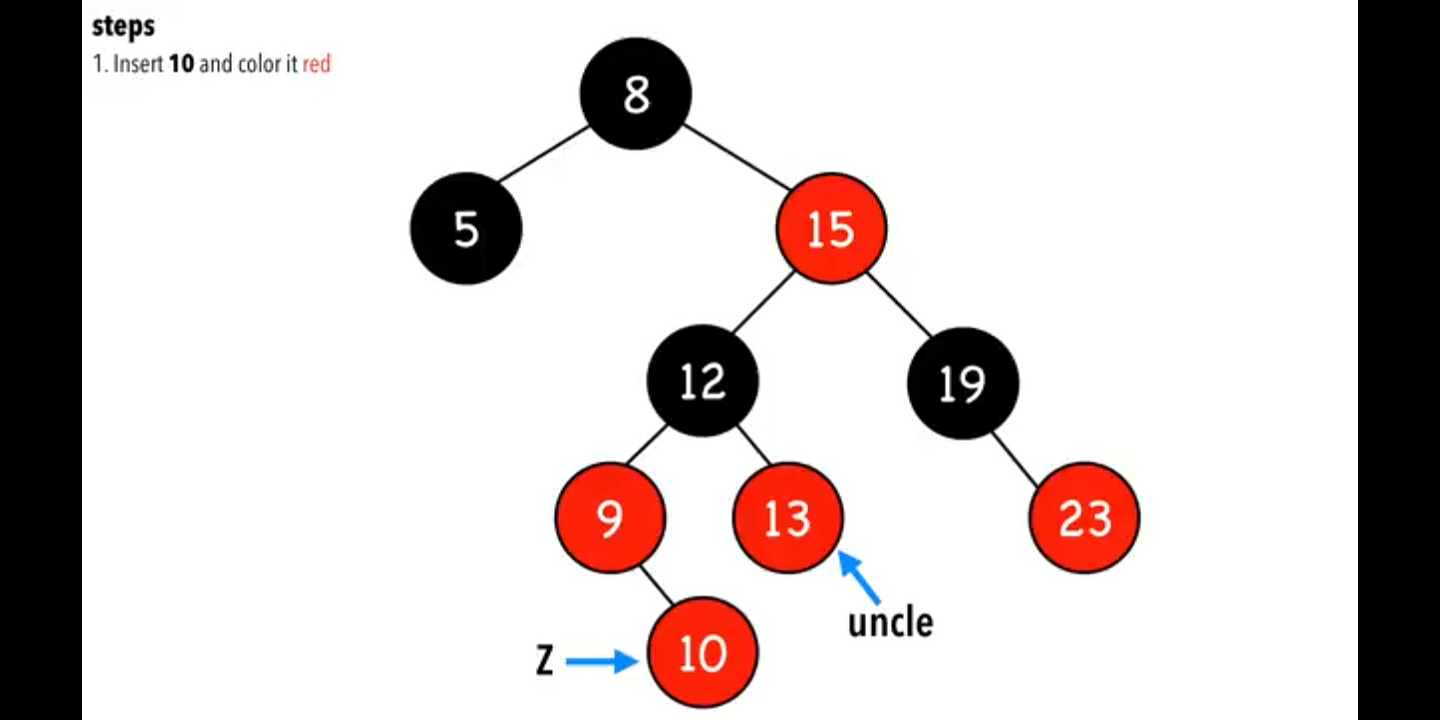
把Z.parent 变成黑色,Z.uncle变成黑色,为维持从上往下的路径中黑色节点数量不变,需要把Z.grandparent=red
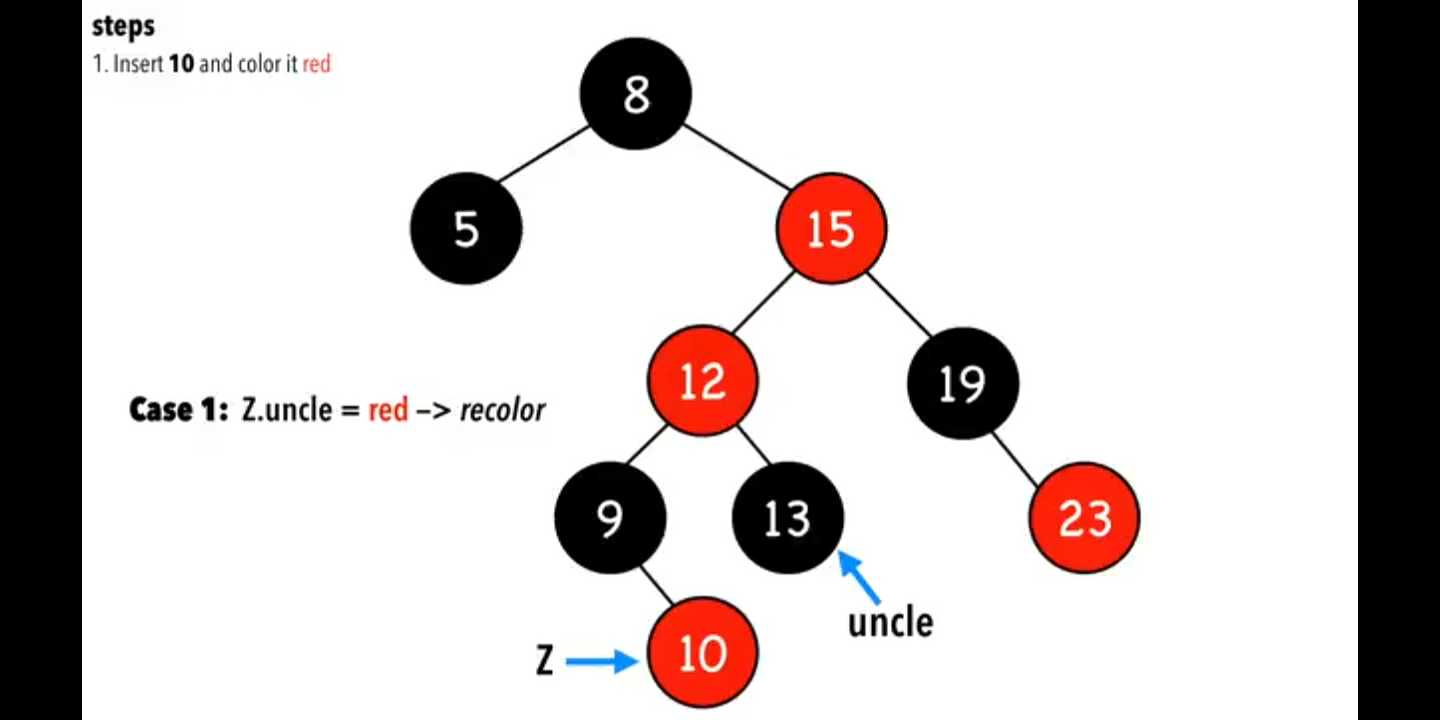
case 3,叔叔节点黑色,而且是三角形的,如图
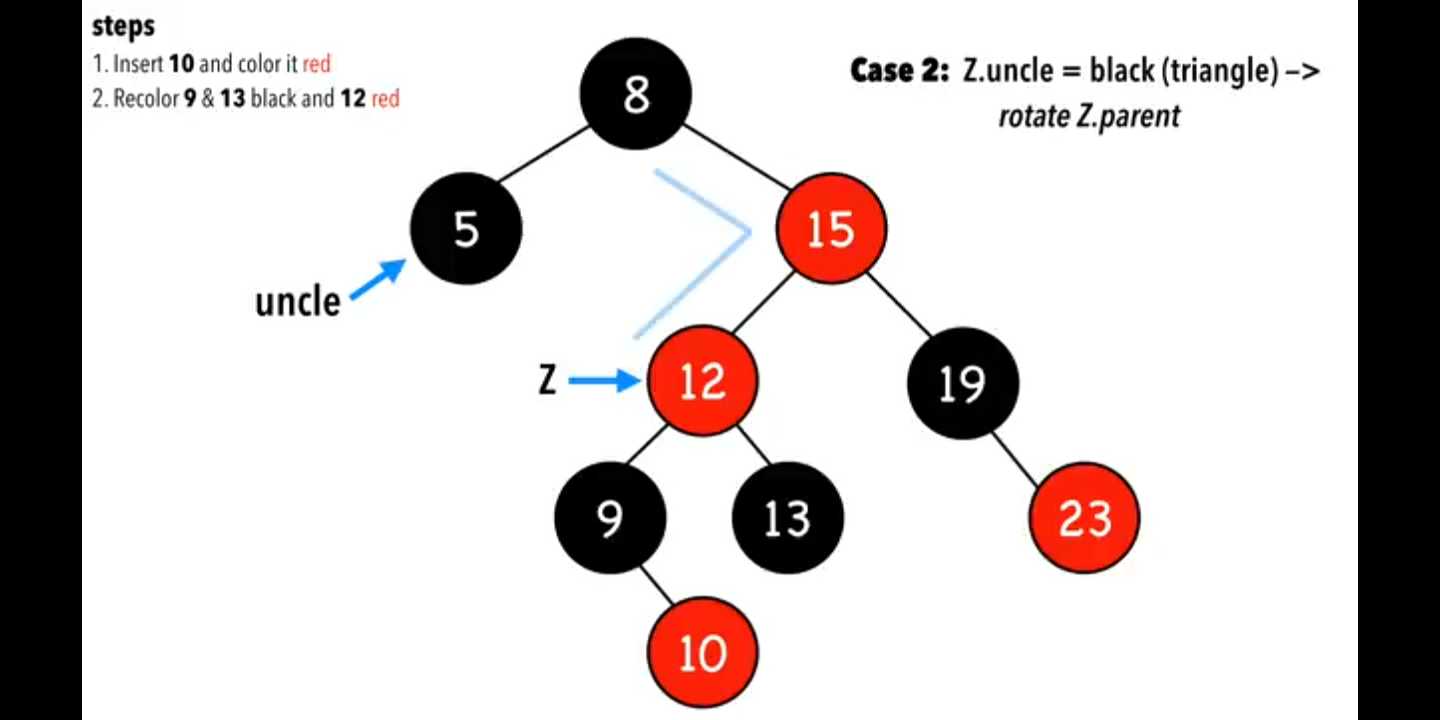
把Z.parent旋转
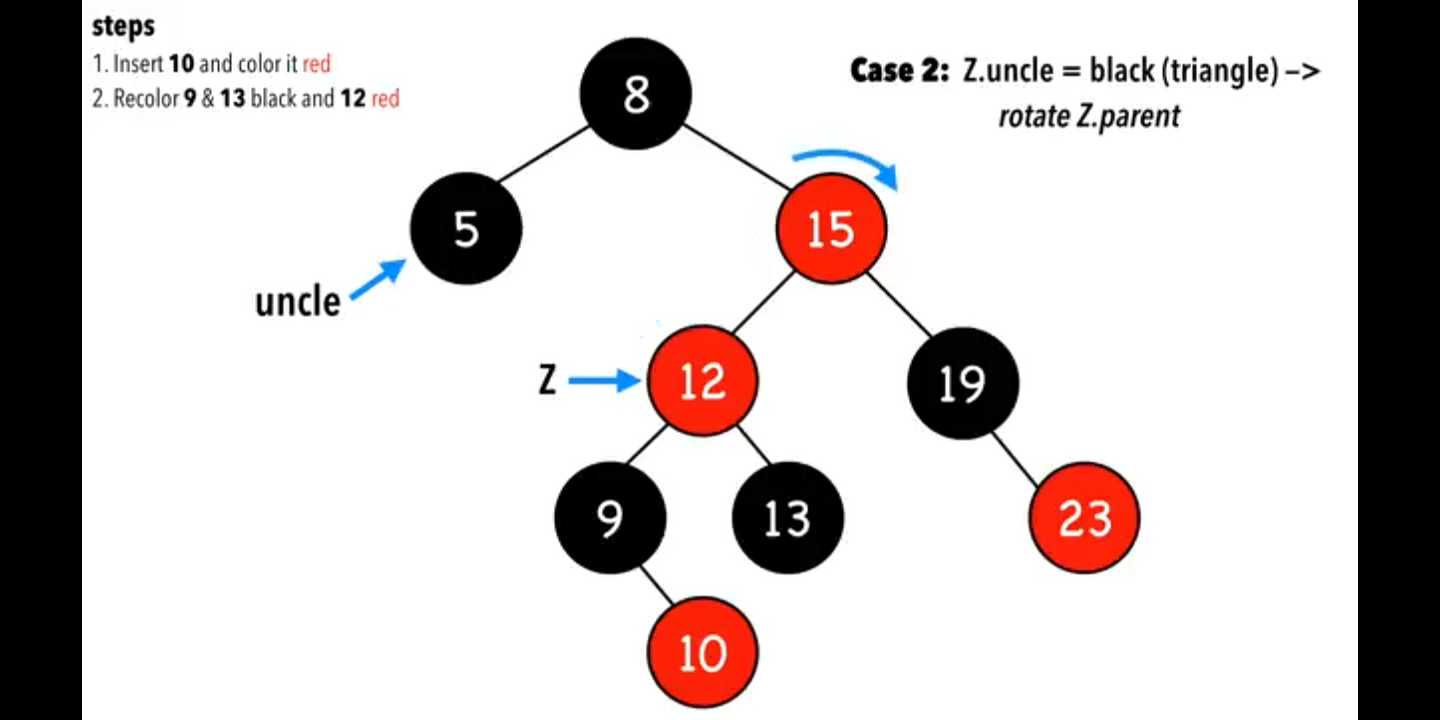
结果如下
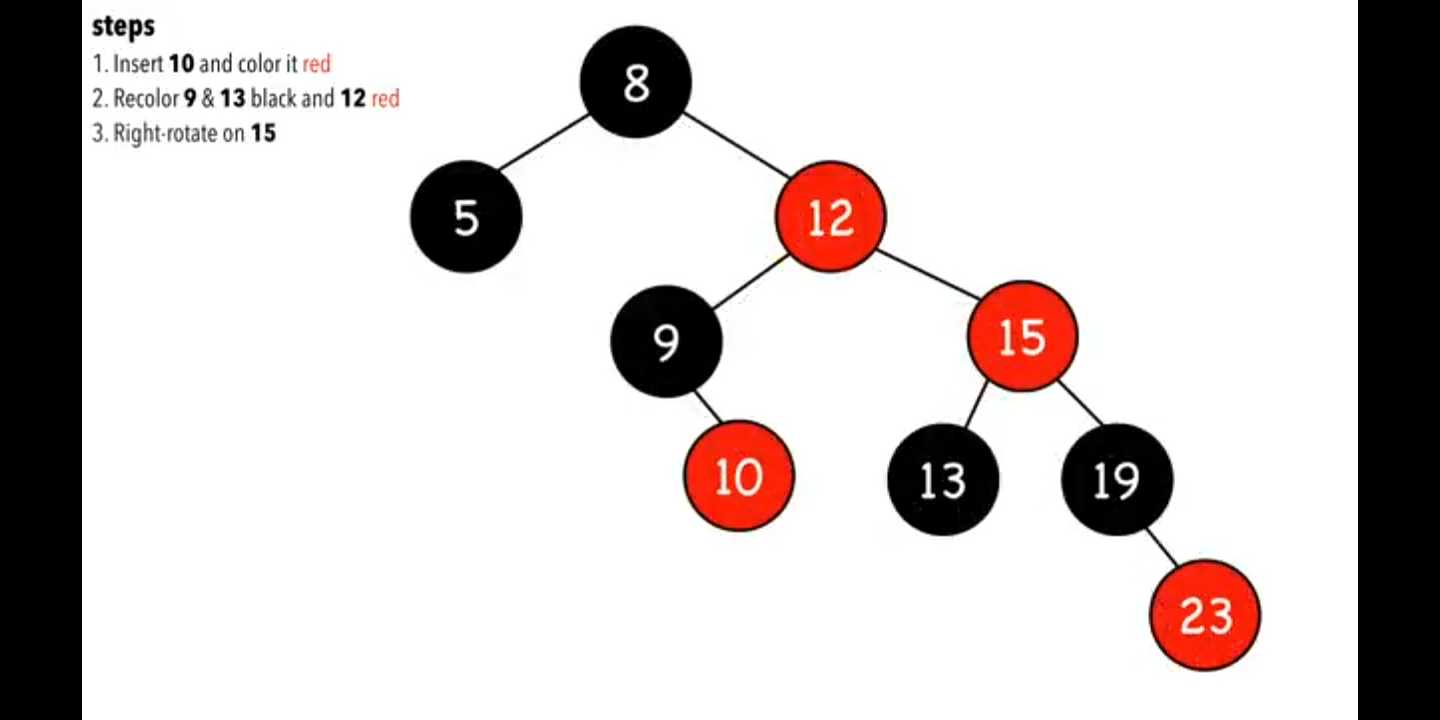
case 5,叔叔节点黑色,而且是线性的,如图
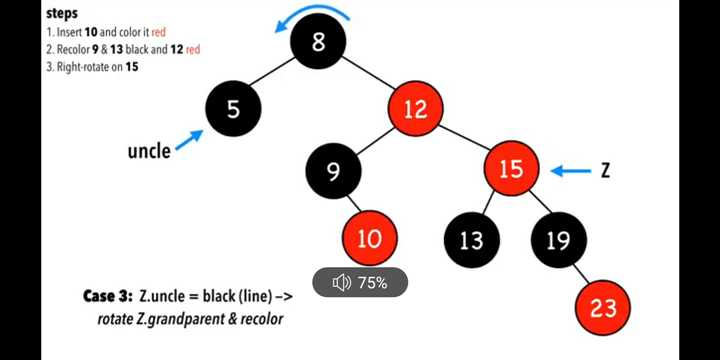
旋转Z的祖父节点,rotate the Z.grandparent,如图:
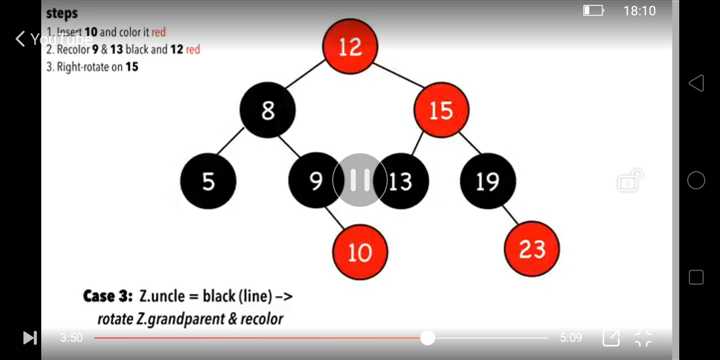
把旋转后的重新着色
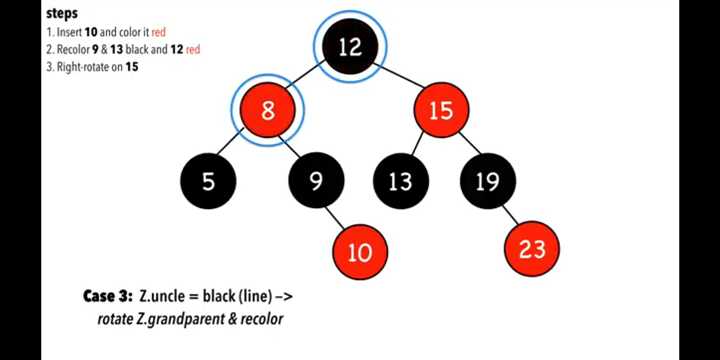
4总结
红黑树的插入元素,总的来说分两部,先旋转,再着色。旋转把RL和LR型变成RR或者LL型,然后再旋转上一级元素;着色要满足红黑树的特性
参考文献
https://en.wikipedia.org/wiki/Red%E2%80%93black_tree
以上是关于5分钟学会红黑树插( insertint elements into a red black tree)的主要内容,如果未能解决你的问题,请参考以下文章