这,就是红黑树!
Posted 雷鸟风曝
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了这,就是红黑树!相关的知识,希望对你有一定的参考价值。
雷鸟内部知识沉淀分享
第6篇-《这,就是红黑树!》吴圣举
(预计“悦读”23分钟)
引言

红黑树是一种数据结构,其在百度百科中的定义:红黑树(Red Black Tree)是一种自平衡二叉树,其与AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
虽然相对比较复杂,其效率在实践中比较高效,对于N个元素的红黑树,可以在O(log n)时间内查找、插入和删除。
从上面的定义可以看出红黑树是一个二叉查找树,那么它的哪些特性保证了其能保证自平衡,而且相对高效呢?下面就介绍下红黑树的特性,首先红黑树是特殊的二叉查找树,即红黑树既具有了二叉查找树的特性,而还具有以下特性:
1.每个节点是具有颜色的,要么是黑色要么是红色;
2.根节点的颜色必须是黑色
3.每个叶子节点都是黑色,并且为空节点(还有另外一种说法就是:每个叶子节点都带有两个空的黑色节点(被称为黑哨兵),如果一个节点n只有一个左孩子,那么n的右孩子是一个黑哨兵;如果节点n只有一个右孩子,那么n的左孩子是一个黑哨兵);
4.如果一个节点是红色,则它的子节点必须是黑色
5.从一个节点到该节点的子孙节点所有路径上包含相同数目的黑节点。
对于红黑树的特性,有2点需要注意的是:
1. 在特性3中指定红黑树的每个叶子节点都是空节点,但是在JAVA实现中红黑树将使用Null表示空节点,因此在JAVA中遍历红黑树时看不到黑色的叶子节点,反而看到的叶子节点是红色的。
2. 特性4保证了从根节点到叶子节点的最长路径的长度不会超过任何其他路径的两倍,例如黑色高度为3的红黑树,其最短路径(路径指的是根节点到叶子节点)是2(黑节点-黑节点-黑节点),其最长路径为4(黑节点-红节点-黑节点-红节点-黑节点)。

一、操作详解
上面详细介绍了红黑树的定义及其特性,那么你肯定很好奇,红黑树是怎样实现其插入、删除、遍历等各种操作的呢?
下面将详细分析红黑树的插入与删除操作。
1.插入操作
对于红黑树而言,其插入节点时,假如设定插入的节点的颜色为红色,那么必然违反了特性5,即改变了红黑树的黑高度,那么插入的节点必然只能为红色。对于插入节点颜色为红色时,又存在如下几种情况:
1.1其父节点为黑色
如下图1所示,这种情况下不会破坏红黑树的特性,即不需要做任何特殊的处理。

(图1)
1.2.其父节点为红色,
当其父节点为红色时又会存在以下5种情况:
a) 新增节点叔节点为红色节点
这种情况现对而言比较简单,如下图2所示,只需要修改父、叔的颜色为黑色,祖的颜色为红色,且递归的检查祖节点即可。
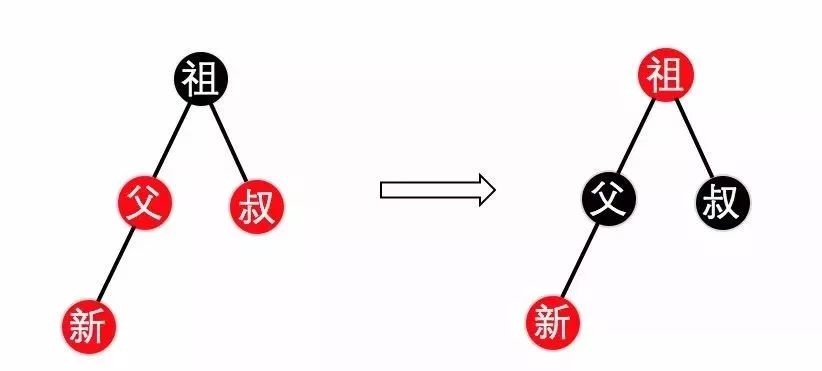
(图2)
b)新增节点叔节点为黑色节点
这种情况比较复杂不能仅通过修改颜色达到平衡的效果,因此需要通过旋转的操作,红黑树有两种旋转操作,左旋与右旋操作。
情况1. 先右旋,在改变颜色(根节点必须为黑色,其两个子节点为红色,叔节点不用改变),如下图3所示,注意省略黑哨兵节点。
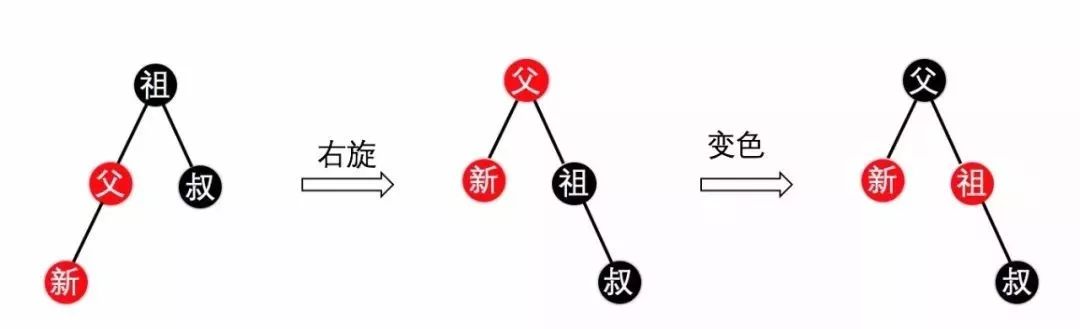
(图3)
情况2. 先左旋变成情况1中的情况,再右旋,最后改变颜色(根节点必须为黑色,其两个子节点为红色,叔节点不用改变),如下图4所示,注意省略黑哨兵节点。
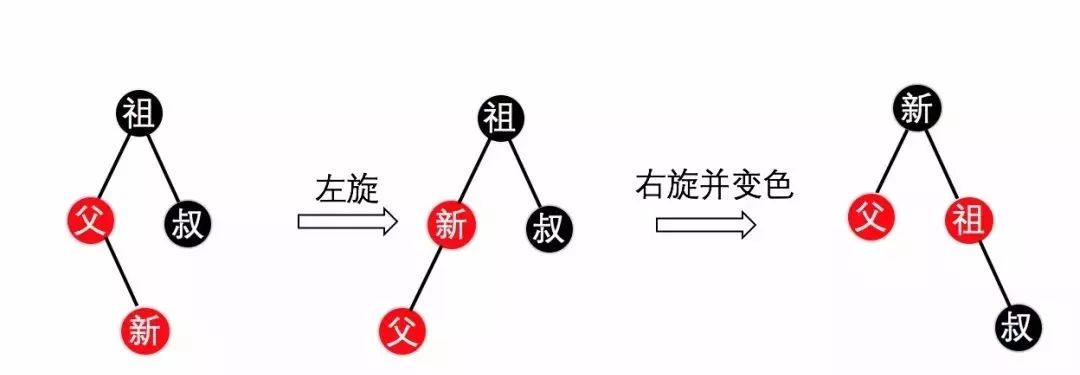
(图4)
情况3. 先左旋,最后改变颜色(根节点必须为黑色,其两个子节点为红色,叔节点不用改变),如下图5所示,注意省略黑哨兵节点。
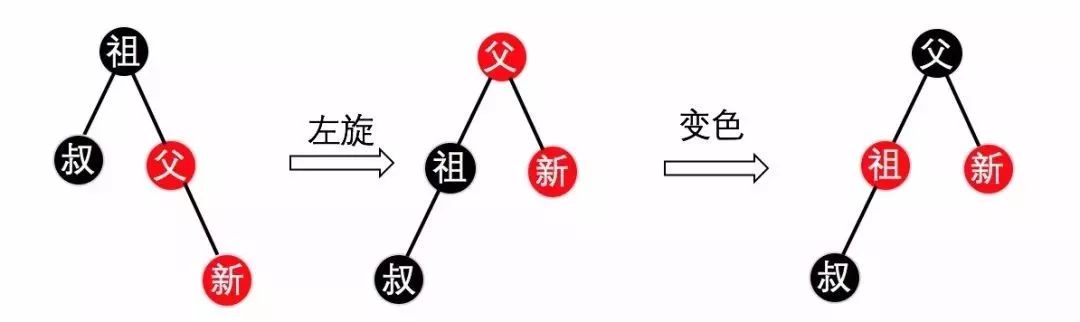
(图5)
情况4. [先右旋变成Case 3的情况,再左旋,最后改变颜色(根节点必须为黑色,其两个子节点为红色,叔节点不用改变),如下图6所示,注意省略黑哨兵节点。
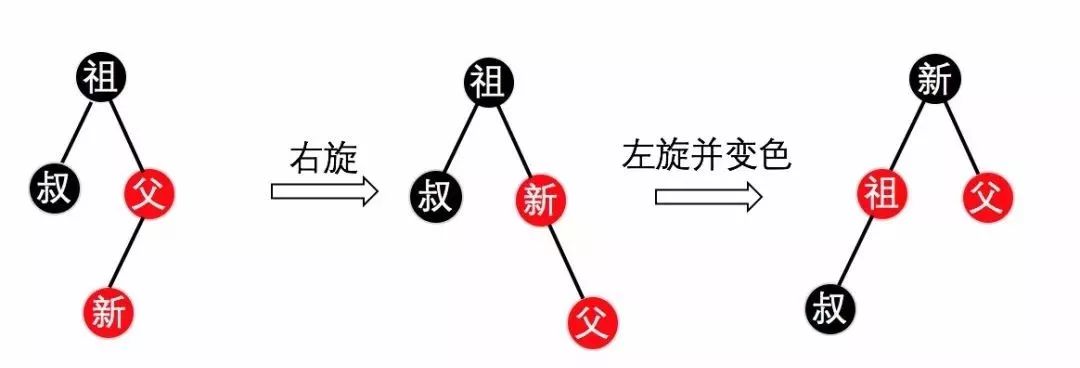
(图6)
以上就是红黑树的新增节点可能的操作情况,可以看出对于新增节点而言,主要通过两种手段改变颜色及自旋操作,来保证红黑树的特性。
2. 删除操作
红黑树的删除操作相比于插入操作要复杂,删除一个节点可以大致分为三种情况:
1) 删除的节点没有孩子节点,即当前节点为叶子节点,直接删除即可;
2) 删除的节点有一个孩子节点,需要删除当前节点,并使用其孩子节点顶替上来;
3) 删除的节点有两个孩子节点,这种需要先找到其后继节点(树中大于节点的最小的元素);然后将其后继节点的内容复制到该节点上,其后继节点就相当于该节点的替身,需要注意的是其后继节点一定不会有两个孩子节点(这点应该很好理解,如果后继节点有左孩子节点,那么当前的后继节点肯定不是最小的,说明后继节点只能存在没有孩子节点或者只有一个右孩子节点),即这样就将问题转换成为1,2中的方式。
在讲解删除操作后修复方式之前,首先需要明白两点:
a. 对于红黑树而言,单支节点的情况只有如下图所示的一种情况,即为当前节点为黑色,其孩子节点为红色,(①假设当前节点为红色,其两个孩子节点必须为黑色;②若有孙子节点,则必为黑色,导致黑子数量不等,而红黑树不平衡)。
b.由于红黑树是特殊的二叉查找树,它的删除和二叉查找树类型,真正的删除点即为删除点A的中序遍历的后继(前继也可以),通过红黑树的特性可知这个后继必然最多只能有一个孩子,其这个孩子节点必然是右孩子节点,从而为单支情况(即这个后继节点只能有一个红色孩子或没有孩子)。
下面将详细介绍,在执行删除节点操作之后,怎样通过修复操作使得红黑树达到平衡。具体情况分为如下几种:
情况1. 被删除的节点为红色,则这节点必定为叶子节点(首先这里的被删除的节点指的是真正删除的节点,通过上文得知的真正删除的节点要么是节点本身,要么是其后继节点,若是节点本身则必须为叶子节点,不为叶子节点的话其会有左右孩子,则真正删除的是其右孩子树上的最小值,若是后继节点,也必须为叶子节点,若不是则其也会有左右孩子,从而和2中相违背),这种情况下删除红色叶节点就可以了,不用进行其他的操作了。如下图7所示。
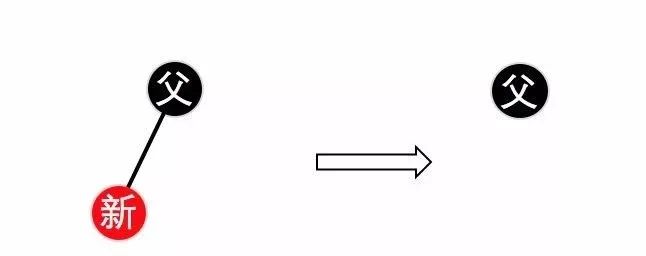
(图7)
情况2. 被删除的节点是黑色,其子节点是红色,将其子节点顶替上来并改变其颜色为黑色,如下图8所示。
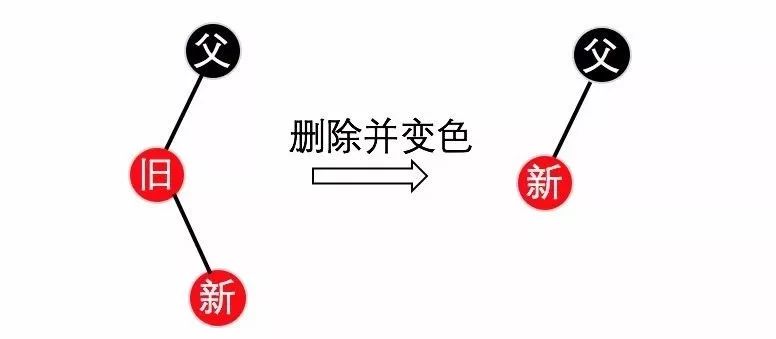
(图8)
情况3. 被删除的节点是黑色,其子节点也是黑色,将其子节点顶替上来,变成了双黑的问题,此时有以下情况:
a) 新节点的兄弟节点为红色,此时若新节点在左边则做左旋操作,否则做右旋操作,之后再将其父节点颜色改变为红色,兄弟节点变为黑色。如下图9/10所示。

(图9)

(图10)
b)新节点的兄弟节点为黑色,此时可能有如下情况:
红父二黑侄:将父节点变成黑色,兄弟节点变成红色,新节点变成黑色即可,如下图11/12所示。
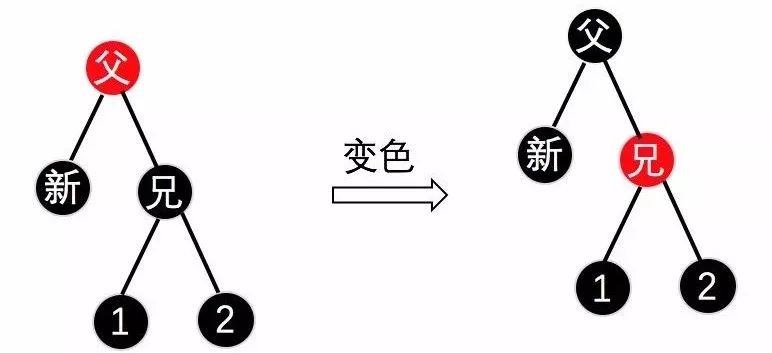
(图11)
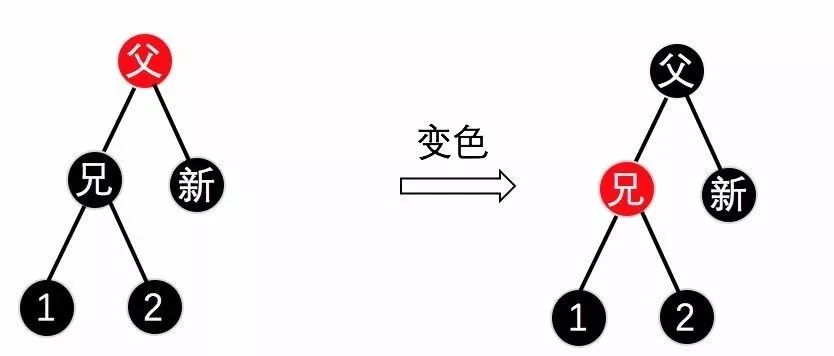
(图12)
黑父二黑侄:
将父节点变成新节点的颜色,新节点变成黑色,兄弟节点染成红色,还需要继续以父节点为判定点继续判断,如下图13/14所示。
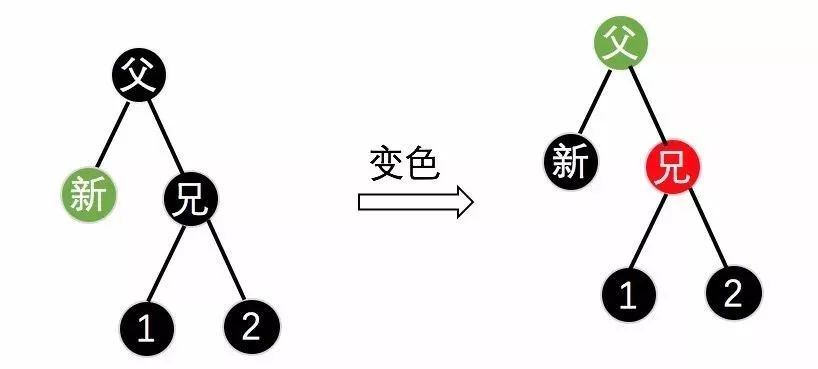
(图13)
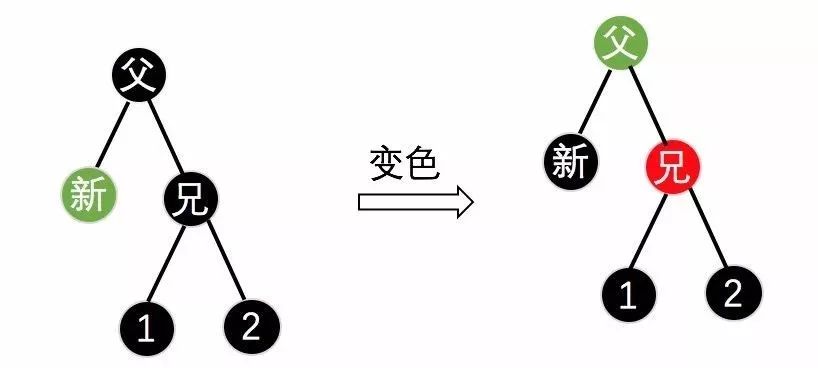
(图14)
红侄:
(1) 新节点在右子树,红侄在兄弟节点左子树,此时的操作为右旋,并将兄弟节点变为父亲的颜色,父亲节点变为黑色,侄节点变为黑色,如下图15所示。
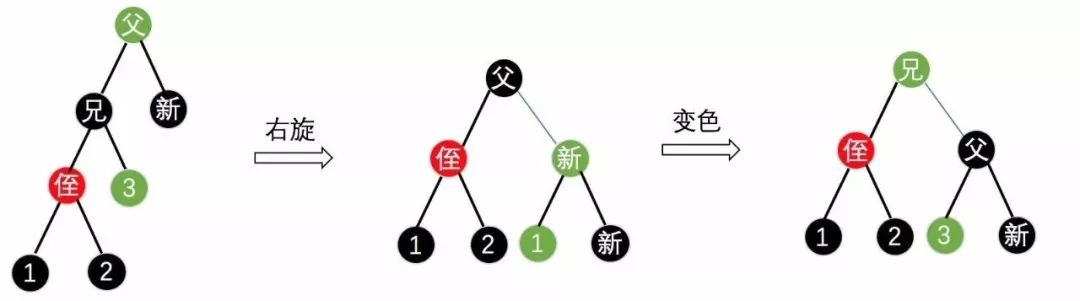
(图15)
(2) 新节点在右子树,红侄在兄弟节点右子树,此时的操作为先左旋,后右旋并将侄节点变为父亲的颜色,父节点变为黑色,如下图16所示。
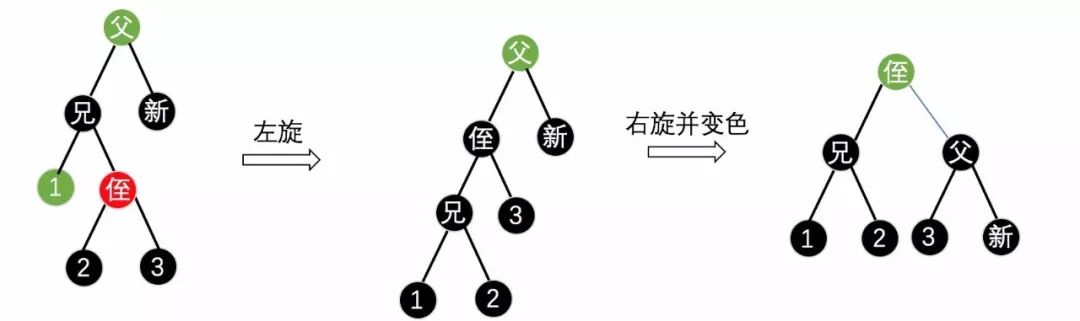
(图16)
(3) 新节点在左子树,红侄在兄弟节点左子树,此时的操作为先右旋在左旋并将侄节点变为父亲的颜色,父亲节点变为黑色,如下图17所示。
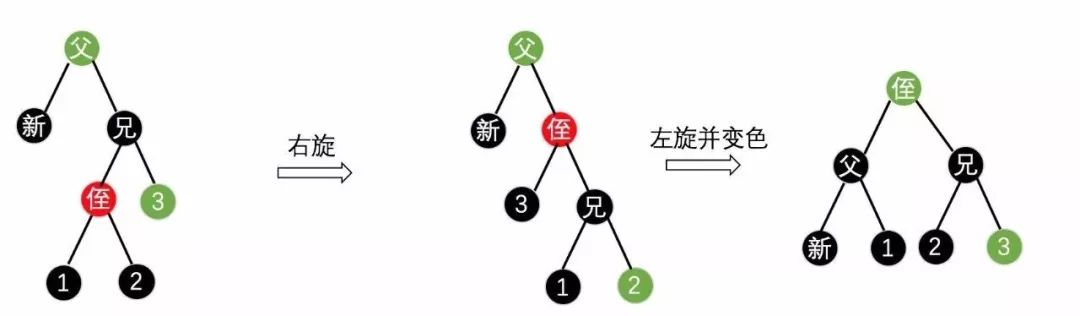
(图17)
(4) 新节点在右子树,红侄在兄弟节点右子树,此时的操作为左旋,并将兄弟节点变为父节点的颜色,父亲节点变为黑色,侄节点变为黑色,如下图18所示。
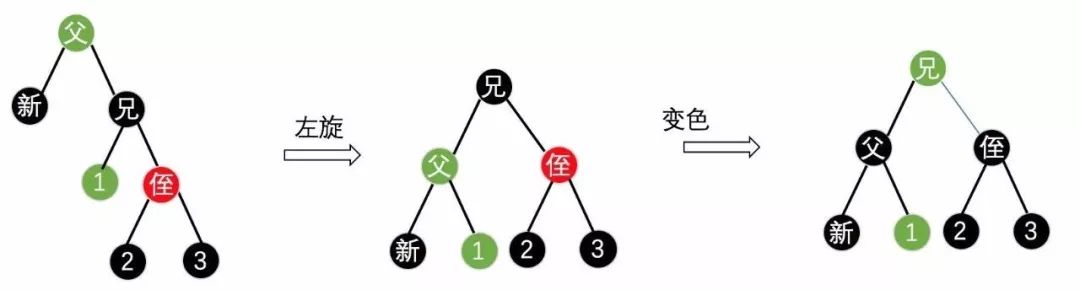
(图18)

二、操作实现
如上介绍了红黑树新增节点与删除节点操作情况,下面将介绍JAVA如何实现红黑树的这些操作。
1.JAVA实现红黑树新增节点操作
如下为JAVA代码实现新增节点操作。
1. /* 插入一个节点
2. * @param node
3. */
4. private void insert(RBTreeNode<T> node){
5. int cmp;
6. RBTreeNode<T> root = this.rootNode;
7. RBTreeNode<T> parent = null;
8. //定位节点添加到哪个父节点下
9. while(null != root){
10. parent = root;
11. cmp = node.key.compareTo(root.key);
12. if (cmp < 0){
13. root = root.left;
14. } else {
15. root = root.right;
16. }
17. }
18. node.parent = parent;
19. //表示当前没一个节点,那么就当新增的节点为根节点
20. if (null == parent){
21. this.rootNode = node;
22. } else {
23. //找出在当前父节点下新增节点的位置
24. cmp = node.key.compareTo(parent.key);
25. if (cmp < 0){
26. parent.left = node;
27. } else {
28. parent.right = node;
29. }
30. }
31. //设置插入节点的颜色为红色
32. node.color = COLOR_RED;
33. //修正为红黑树
34. insertFixUp(node);
35. }
36. /**
37. * 红黑树插入修正
38. * @param node
39. */
40. private void insertFixUp(RBTreeNode<T> node){
41. RBTreeNode<T> parent,gparent;
42. //节点的父节点存在并且为红色
43. while( ((parent = getParent(node)) != null) && isRed(parent)){
44. gparent = getParent(parent);
45. //如果其祖父节点是空怎么处理
46. // 若父节点是祖父节点的左孩子
47. if(parent == gparent.left){
48. RBTreeNode<T> uncle = gparent.right;
49. if ((null != uncle) && isRed(uncle)){
50. setColorBlack(uncle);
51. setColorBlack(parent);
52. setColorRed(gparent);
53. node = gparent;
54. continue;
55. }
56. if (parent.right == node){
57. RBTreeNode<T> tmp;
58. leftRotate(parent);
59. tmp = parent;
60. parent = node;
61. node = tmp;
62. }
63. setColorBlack(parent);
64. setColorRed(gparent);
65. rightRotate(gparent);
66. } else {
67. RBTreeNode<T> uncle = gparent.left;
68. if ((null != uncle) && isRed(uncle)){
69. setColorBlack(uncle);
70. setColorBlack(parent);
71. setColorRed(gparent);
72. node = gparent;
73. continue;
74. }
75. if (parent.left == node){
76. RBTreeNode<T> tmp;
77. rightRotate(parent);
78. tmp = parent;
79. parent = node;
80. node = tmp;
81. }
82. setColorBlack(parent);
83. setColorRed(gparent);
84. leftRotate(gparent);
85. }
86. }
87. setColorBlack(this.rootNode);
88. }
如上源码所示,插入节点操作主要分为两步:
第一步:定位
也就是遍历整个红黑树,确定添加的位置,如上代码中insert方法中就是在找到节点添加的位置;
第二步:修复
正如第二节中介绍的,新增节点之后可能会导致红黑树不能满足其特性,这时需要通过变色、旋转来调整红黑树,代码中insertFixUp方法就是执行这个过程。
2.JAVA实现红黑树删除节点操作
如下为JAVA实现红黑树删除节点的操作,主要分为下面的操作
2.1 删除节点:按照如下三种情况处理:
a)真正删除的节点没有子节点;
b)真正删除的节点有一个子节点
c)真正删除的节点有两个子节点
2.2 修复红黑树特性,如代码中调用removeFixUp方法修复。
3. private void remove(RBTreeNode<T> node){
4. RBTreeNode<T> child,parent;
5. boolean color;
6. //被删除节点左右孩子都不为空的情况
7. if ((null != node.left) && (null != node.right)){
8. //获取到被删除节点的后继节点
9. RBTreeNode<T> replace = node;
10. replace = replace.right;
11. while(null != replace.left){
12. replace = replace.left;
13. }
14. //node节点不是根节点
15. if (null != getParent(node)){
16. //node是左节点
17. if (getParent(node).left == node){
18. getParent(node).left = replace;
19. } else {
20. getParent(node).right = replace;
21. }
22. } else {
23. this.rootNode = replace;
24. }
25. child = replace.right;
26. parent = getParent(replace);
27. color = getColor(replace);
28. if (parent == node){
29. parent = replace;
30. } else {
31. if (null != child){
32. setParent(child,parent);
33. }
34. parent.left = child;
35. replace.right = node.right;
36. setParent(node.right, replace);
37. }
38. replace.parent = node.parent;
39. replace.color = node.color;
40. replace.left = node.left;
41. node.left.parent = replace;
42. if (color == COLOR_BLACK){
43. removeFixUp(child,parent);
44. }
45. node = null;
46. return;
47. }
48. if (null != node.left){
49. child = node.left;
50. } else {
51. child = node.right;
52. }
53. parent = node.parent;
54. color = node.color;
55. if (null != child){
56. child.parent = parent;
57. }
58. if (null != parent){
59. if (parent.left == node){
60. parent.left = child;
61. } else {
62. parent.right = child;
63. }
64. } else {
65. this.rootNode = child;
66. }
67. if (color == COLOR_BLACK){
68. removeFixUp(child, parent);
69. }
70. node = null;
71. }
72. /**
73. * 删除修复
74. * @param node
75. * @param parent
76. */
77. private void removeFixUp(RBTreeNode<T> node, RBTreeNode<T> parent){
78. RBTreeNode<T> other;
79. //node不为空且为黑色,并且不为根节点
80. while ((null == node || isBlack(node)) && (node != this.rootNode) ){
81. //node是父节点的左孩子
82. if (node == parent.left){
83. //获取到其右孩子
84. other = parent.right;
85. //node节点的兄弟节点是红色
86. if (isRed(other)){
87. setColorBlack(other);
88. setColorRed(parent);
89. leftRotate(parent);
90. other = parent.right;
91. }
92. //node节点的兄弟节点是黑色,且兄弟节点的两个孩子节点也是黑色
93. if ((other.left == null || isBlack(other.left)) &&
94. (other.right == null || isBlack(other.right))){
95. setColorRed(other);
96. node = parent;
97. parent = getParent(node);
98. } else {
99. //node节点的兄弟节点是黑色,且兄弟节点的右孩子是红色
100. if (null == other.right || isBlack(other.right)){
101. setColorBlack(other.left);
102. setColorRed(other);
103. rightRotate(other);
104. other = parent.right;
105. }
106. //node节点的兄弟节点是黑色,且兄弟节点的右孩子是红色,左孩子是任意颜色
107. setColor(other, getColor(parent));
108. setColorBlack(parent);
109. setColorBlack(other.right);
110. leftRotate(parent);
111. node = this.rootNode;
112. break;
113. }
114. } else {
115. other = parent.left;
116. if (isRed(other)){
117. setColorBlack(other);
118. setColorRed(parent);
119. rightRotate(parent);
120. other = parent.left;
121. }
122. if ((null == other.left || isBlack(other.left)) &&
123. (null == other.right || isBlack(other.right))){
124. setColorRed(other);
125. node = parent;
126. parent = getParent(node);
127. } else {
128. if (null == other.left || isBlack(other.left)){
129. setColorBlack(other.right);
130. setColorRed(other);
131. leftRotate(other);
132. other = parent.left;
133. }
134. setColor(other,getColor(parent));
135. setColorBlack(parent);
136. setColorBlack(other.left);
137. rightRotate(parent);
138. node = this.rootNode;
139. break;
140. }
141. }
142. }
143. if (node!=null)
144. setColorBlack(node);
145. }
三、应用
熟悉JAVA的同学可能知道,JDK1.8中HashMap的底层结构由以前的链表引入了红黑树,那么下面就对比下JDK1.7HashMap 与引入红黑树之后的区别。如下表所示分别为Hash较均匀的情况,以及Hash不均匀的情况
1. Hash较均匀的情况
表1

2.Hash不均匀的情况
表2

从表格中可以看出JDK1.8的性能要高于JDK1.715%以上,在某些size的区域上,甚至高于100%。当Hash算法较均匀,JDK1.8引入的红黑树效果不明显,当Hash不均匀的时,随着size的变大,JDK1.7的花费时间是增长的趋势,而JDK1.8是明显的降低趋势,并且呈现对数增长稳定。当一个链表太长的时候,HashMap会动态的将它替换成一个红黑树,这会将时间复杂度从O(n)降为O(logn),极大的提高了性能。
总结
作为平衡二叉查找树里面众多的实现之一,红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念,通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树,旋转是一个必不可少的操作。通过旋转可以降低树的高度,在红黑树里面还可以转换颜色。
红黑树里面的插入和删除的操作比较难理解,这时要注意记住一点:操作之前红黑树是平衡的,颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色,要达到这个目的,就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转,一旦借调了别的节点,删除和插入的节点就会达到局部的平衡(局部符合红黑树的定义),但是被借调的节点就不会平衡了,这时就需要以被借调的节点为起点继续进行调整,直到整棵树都是平衡的。在整个修复的过程中,插入具体的分为3种情况,删除分为4种情况。
整个红黑树的查找,插入和删除都是O(logN)的,原因就是整个红黑树的高度是logN,查找从根到叶,走过的路径是树的高度,删除和插入操作是从叶到根的,所以经过的路径都是logN。

从4月开始,雷鸟风曝的“悦读书吧”板块,每周会定期给大家推送内部伙伴的知识分享,欢迎大家阅读分享及留言喔~
如果你也有想与我们分享的,欢迎投稿到yedc@ffalcon.cn
我们一起“悦读”吧~
可以通过扫描以下二维码关注,谢谢~
雷鸟风曝
(雷鸟的大喇叭)
以上是关于这,就是红黑树!的主要内容,如果未能解决你的问题,请参考以下文章