SVM原理
Posted zwjhq
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SVM原理相关的知识,希望对你有一定的参考价值。
- SVM的原理是什么?
有别于感知机,SVM在特征空间中寻找间隔最大化的分离超平面的线性分类器 - SVM为什么采用间隔最大化?
超平面可以有无穷多个,但是几何间隔最大的分离超平面是唯一的,这样的分类结果也是鲁棒的,对未知实例的泛化能力最强。 - 什么是支持向量?
对于硬间隔,支持向量就是间隔边界上的样本点
对于软间隔,支持向量就是间隔边界、间隔带内、分离超平面误分类一侧的样本点
在确定分类超平面时只有支持向量起作用,因此SVM由很少的“重要的“训练样本确定 - 为什么要将SVM的原始问题转化为对偶问题?
更容易求解(引入拉格朗日乘子,将约束优化转化为无约束优化问题)
引入核函数 (?(x)?(x)?(x)?(x)),推广到非线性分类 - 为什么要scale the inputs?(对数据进行归一化处理)
SVM对特征规模非常敏感,如果不对特征进行规范化,会导致生成的间隔带依赖于scale大的那个特征,即生成不合适的svm - 为什么SVM对缺失数据敏感?
不同于决策树,SVM没有处理缺失值的策略,它希望样本在特征空间中线性可分,所以特征空间的好坏对SVM的性能很重要 - 什么是核函数?
当样本在原始空间线性不可分时,可以将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。这个映射函数我们记为?(x)?(x)
在原始问题的对偶问题中需要求解?(x)?(y)?(x)?(y),直接计算比较困难,因此找一个核函数k(x,y)=?(x)?(y)k(x,y)=?(x)?(y),即在特征空间的内积等于它们在原始样本空间中进行核函数kk计算 - 常用的核函数有哪些,如何选择?
- RBF核/高斯核 : k(xi,xj)=exp(?||xi?xj||22σ2)k(xi,xj)=exp(?||xi?xj||22σ2),其中σσ为高斯核的带宽
- 多项式核: k(xi,xj)=(xTixj)dk(xi,xj)=(xiTxj)d,当d=1时退化为线性核
- 拉普拉斯核:k(xi,xj)=exp(?||xi?xj||2σ)k(xi,xj)=exp(?||xi?xj||2σ)
- Sigmoid核:k(xi,xj)=tanh(βxTixj+θ)k(xi,xj)=tanh(βxiTxj+θ)
- 字符串核
选择方法:经验+实验
(吴恩达)
如果Feature的数量很大,跟样本数量差不多,LR or Linear Kernel SVM
如果Feature的数量比较小,样本数量一般,不大不小,Gaussian Kernel SVM
如果Feature的数量比较小,而样本数量很多,手工添加Feature+LR or Linear Kernel SVM
- 如果一个SVM用RBF导致过拟合了,应该如何调整σσ和C的值?
RBF的外推能力随着σσ的增加而减小,相当于映射到一个低维的子空间,如果σσ很小,则可以将任意的数据线性可分,但是会产生过拟合问题,因此要增大σσ和减小CC - 为什么说SVM是结构风险最小化模型?
SVM在目标函数中有一项12||w||212||w||2,它自带正则 - SVM如何处理多分类问题?
one vs one
one vs 多,bias 较高 - SVM和LR的比较
- 样本点对模型的作用不同,SVM仅支持向量(少量样本点)而LR是全部样本点
- 损失函数不同,SVM hinge LR log
- 输出不同。 LR可以有概率值,而SVM没有
- 过拟合能力不同。 SVM 自带正则,LR要添加正则项
- 处理分类问题能力不同。 SVM 二分类,需要 one vs one or one vs all 。 LR可以直接进行多分类
- 计算复杂度。 海量数据中SVM效率较低
- 数据要求。 SVM需要先对样本进行标准化
- 能力范围。 SVM 可以用于回归
- KKT条件
- 支撑平面:和支持向量相交的平面;分割平面:支撑平面中间的平面(最优分类平面)
- SVM不是定义损失,而是定义支持向量之间的距离为目标函数
- 正则化参数对支持向量数的影响:
正则化参数越大,说明惩罚越多,则支持向量数越少 - 感知机 (判别模型)
目标函数:f(x)=sign(ωx+b)f(x)=sign(ωx+b)
损失函数:L(ω,b)=?∑xi∈Myi(ωxi+b)L(ω,b)
解决方法:随机梯度下降,每一次随机选取一个误分类点使其梯度下降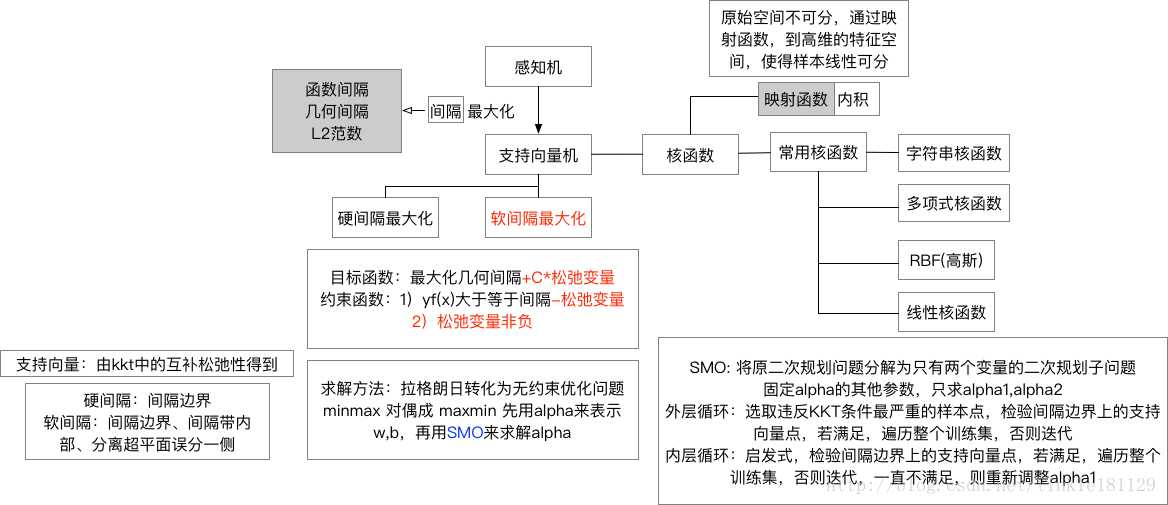
-
以上是关于SVM原理的主要内容,如果未能解决你的问题,请参考以下文章