6.支持向量机(SVM)什么是SVM支持向量机基本原理与思想基本原理课程中关于SVM介绍
Posted to.to
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了6.支持向量机(SVM)什么是SVM支持向量机基本原理与思想基本原理课程中关于SVM介绍相关的知识,希望对你有一定的参考价值。
6.支持向量机(SVM)
6.1.什么是SVM
6.2.支持向量机基本原理与思想
6.2.1.支持向量机
6.2.2.基本原理
6.3.课程中关于SVM介绍
6.支持向量机(SVM)
6.1.什么是SVM
以下转自:https://www.zhihu.com/question/21094489
支持向量机/support vector machine (SVM)。
可以从一个了解什么是SVM,以及要做的事情。
在很久以前的情人节,大侠要去救他的爱人,但魔鬼和他玩了一个游戏。
魔鬼在桌子上似乎有规律放了两种颜色的球,说:“你用一根棍分开它们?要求:尽量在放更多球之后,仍然适用。”

于是大侠这样放,干的不错?

然后魔鬼,又在桌上放了更多的球,似乎有一个球站错了阵营。
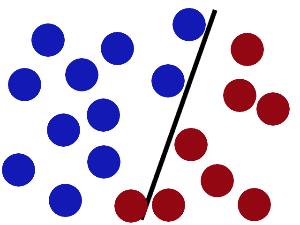
SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能大的间隙。
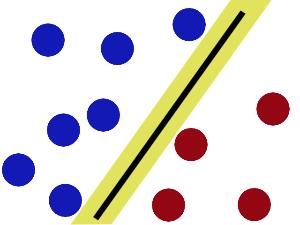
现在即使魔鬼放了更多的球,棍仍然是一个好的分界线。

然后,在SVM 工具箱中有另一个更加重要的 trick。 魔鬼看到大侠已经学会了一个trick,于是魔鬼给了大侠一个新的挑战。
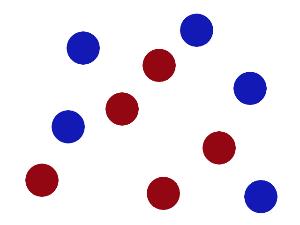
现在,大侠没有棍可以很好帮他分开两种球了,现在怎么办呢?当然像所有武侠片中一样大侠桌子一拍,球飞到空中。然后,凭借大侠的轻功,大侠抓起一张纸,插到了两种球的中间。
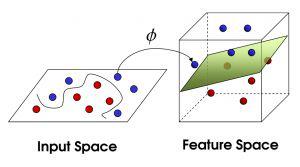
现在,从魔鬼的角度看这些球,这些球看起来像是被一条曲线分开了。
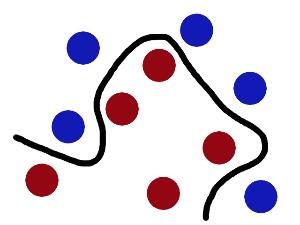
再之后,无聊的大人们,把这些球叫做**「data」,把棍子 叫做「classifier」, 最大间隙trick 叫做「optimization」, 拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」**
6.2.支持向量机基本原理与思想
6.2.1.支持向量机
SVM即支持向量机(Support Vector Machine),是有监督学习算法的一种,用于解决数据挖掘或模式 识别领域中数据分类问题。
6.2.2.基本原理
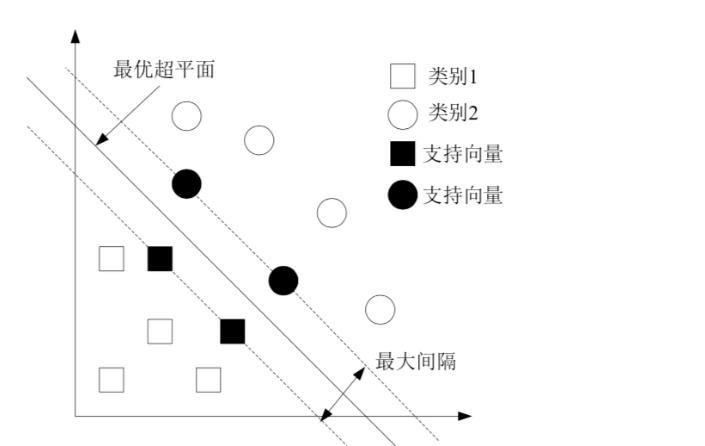
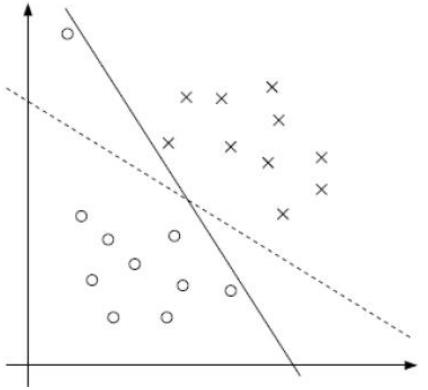
SVM算法 即寻找一个分类器使得超平面和最近的数据点之间的分类边缘(超平面和最近的数据点之间的 间隔被称为分类边缘)最大,对于SVM算法通常认为分类边缘越大,平面越优,通常定义具有“最大间隔”的决策面就是 SVM 要寻找的最优解。并且最优解对应两侧虚线要穿过的样本点,称为“支持向量”。其处理的基本思路为:把问题转化为一个凸二次规划 问题,可以用运筹学有关思想进行求解:
(1)目标函数
在线性SVM算法中,目标函数显然就是那个"分类间隔",使分类间隔最大。
(2)约束条件
即决策面,通常需要满足三个条件:
1)确定决策面使其正确分类。
2)决策面在间隔区域的中轴线。
3)如何确定支持向量因此求解SVM问题即转化为求解凸二次规划的最优化问题。
支持向量机:就是用来分割数据点那个分割面,他的位置是由支持向量确定的(如果支持 向量发生了变化,往往分割面的位置也会随之改变), 因此这个面就是一个支持向量确定的 分类器即支持向量机。
线性可分数据的二值分类机理:系统随机产生一个超平面并移动它,直到训练集中属于不同类别的样本点正好位于该超平面的两侧。显然,这种机理能够解决线性分类问题,但不能够保证产生的超平面是最优的。支持向量机建立的分类超平面能够在保证分类精度的同时, 使超平面两侧的空白区域最大化,从而实现对线性可分问题的最优分类。
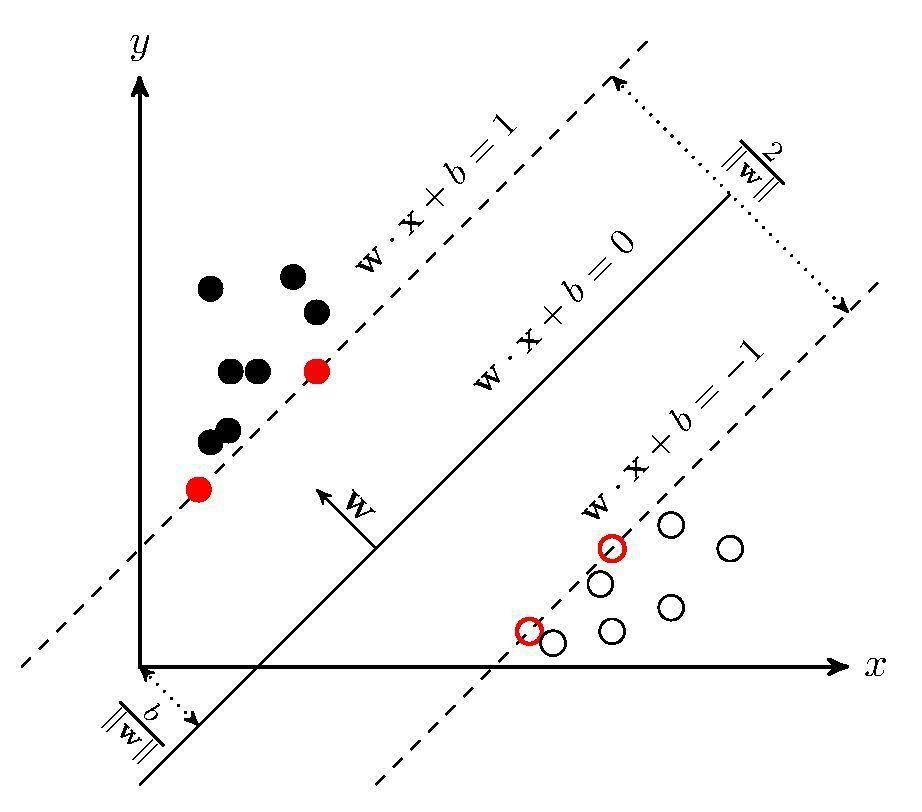
SVM的主要思想是:建立一个最优决策超平面,使得该平面两侧距平面最近的两类样 本之间的距离最大化,从而对分类问题提供良好的泛化力(推广能力)。
支持向量:则是指训练集中的某些训练点,这些点最靠近分类决策面,是最难分类的数据点。
SVM: 它是一种有监督(有导师)学习方法,即已知训练点的类别,求训练点和类别之间的对应关系,以便将训练集按照类别分开,或者是预测新的训练点所对应的类别。
6.3.课程中关于SVM介绍
Support Vector Machine
- 决策边界:选出来离雷区最远的(雷区就是边界上的点,要Large Margin)
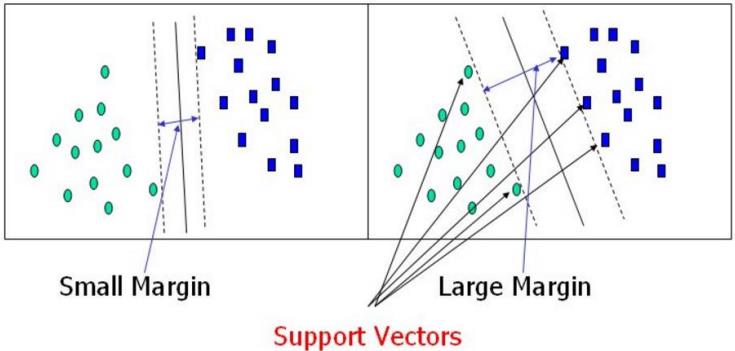
距离的计算
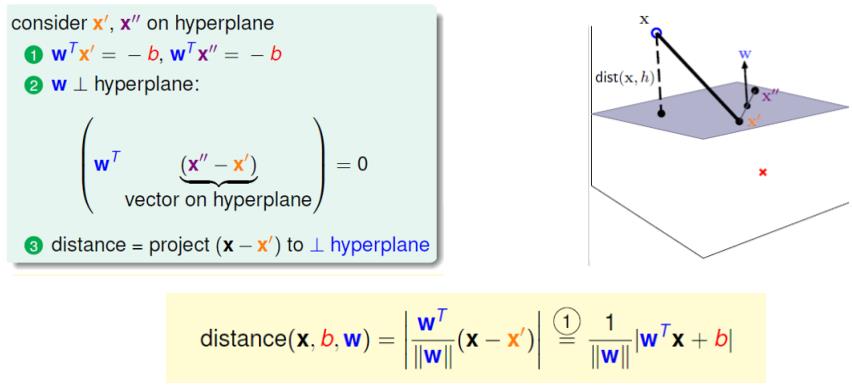






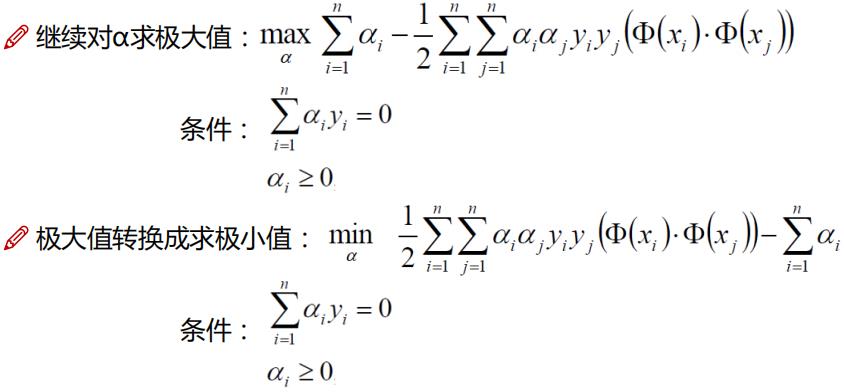
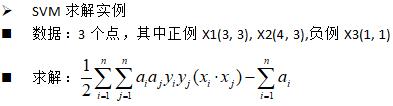
约束条件: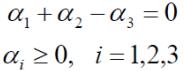
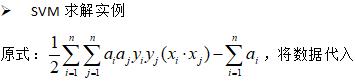
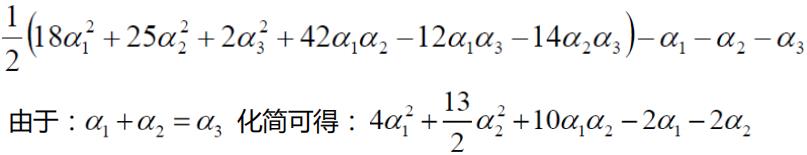


最小值在(0.25, 0, 0.25)处取得
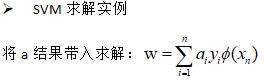
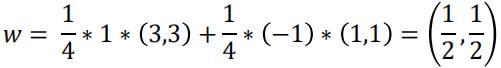
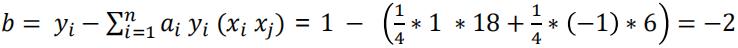
- 平面方程为:
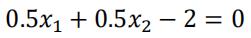
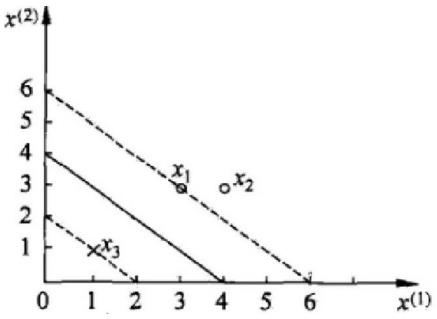
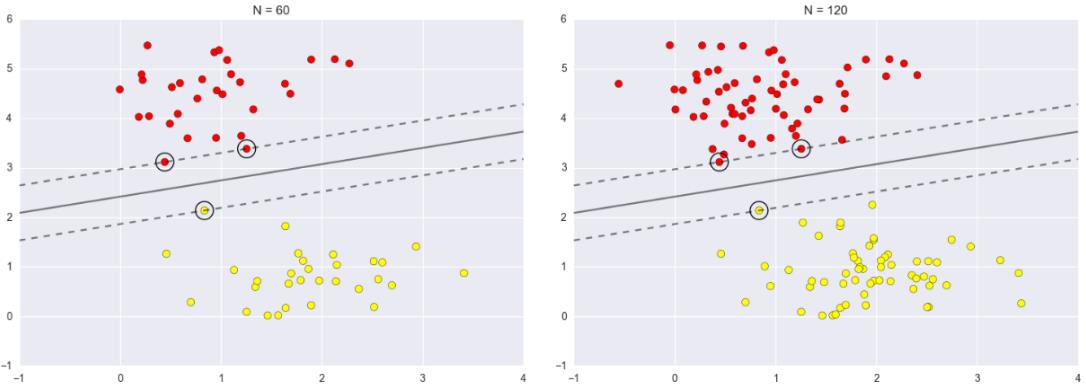
SVM求解实例
支持向量:真正发挥作用的数据点,a值不为0的点。
soft-margin
-
软间隔:有时候数据中有一些噪音点,如果考虑它们咱们的线就不太好了。
-
之前的方法要求要把两类点完全分得开,这个要求有点过于严格了,我们来放松一点!
-
为了解决该问题,引入松弛因子

soft-margin -
新的目标函数:

-
当C趋近于很大时:意味着分类严格不能有错误。
当C趋近于很小时:意味着可以有更大的错误容忍 -
C是我们需要指定的一个参数!

Soft-margin -
拉格朗日乘子法:

低维不可分问题 -
核变换:既然低维的时候不可分,那我给它映射到高维呢?
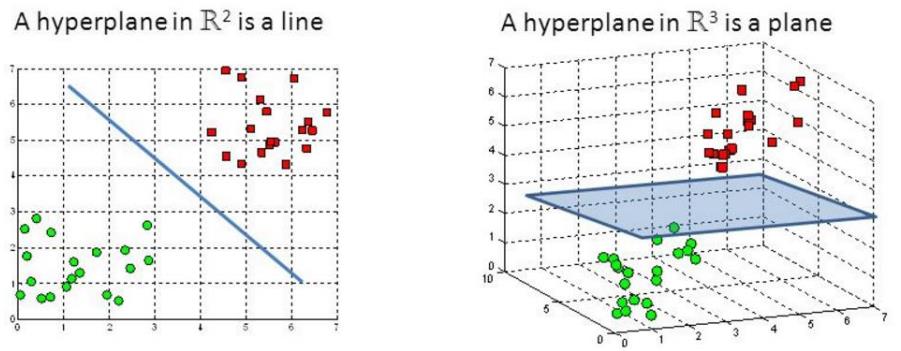
低维不可分问题 -
目标:找到一种变换的方法,也就是

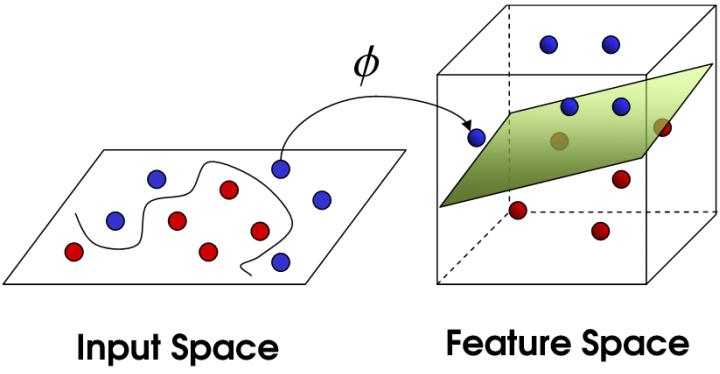
Support Vector Machine
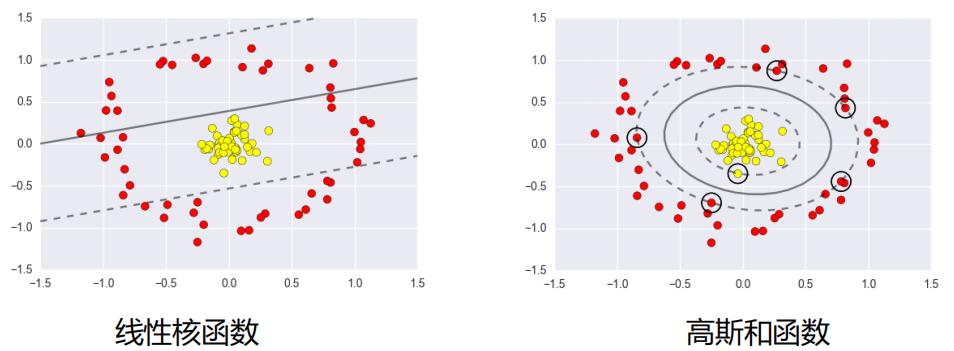
高斯核函数:
以上是关于6.支持向量机(SVM)什么是SVM支持向量机基本原理与思想基本原理课程中关于SVM介绍的主要内容,如果未能解决你的问题,请参考以下文章