动态规划-最长可互除子序列 Largest Divisible Subset

Posted 2021-01-02 timhy

2018-08-28 17:51:04

问题描述：

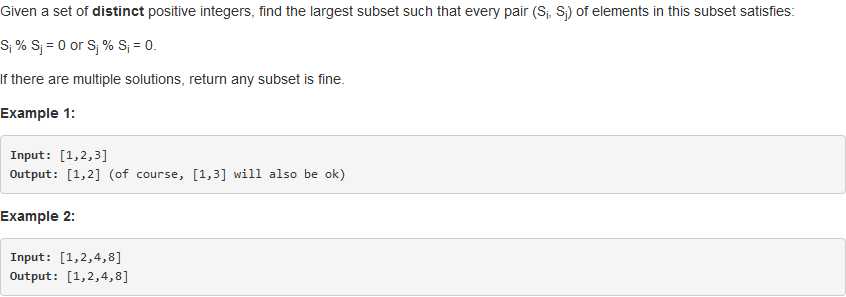
问题求解：

本题是一个求最优解的问题，很自然的会想到动态规划来进行解决。但是刚开始还是陷入了僵局，直到看到了hint：LIS，才有了进一步的思路。下面是最初的一个解法。使用的是map来记录信息。

    public List<Integer> largestDivisibleSubset(int[] nums) {
        if (nums.length == 0) return new ArrayList<>();
        Arrays.sort(nums);
        Map<Integer, List<Integer>> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            List<Integer> tmp = null;
            int maxlen = 0;
            for (int j = 0; j < i; j++) {
                if (nums[i] % nums[j] == 0 && maxlen < map.get(nums[j]).size()) {
                    tmp = new ArrayList<>(map.get(nums[j]));
                    maxlen = tmp.size();
                }
            }
            if (tmp == null) tmp = new ArrayList<>();
            tmp.add(nums[i]);
            map.put(nums[i], tmp);
        }
        int maxlen = 0;
        List<Integer> res = null;
        for (Integer i : map.keySet()) {
            if (map.get(i).size() > maxlen) {
                res = map.get(i);
                maxlen = res.size();
            }
        }
        return res;
    }

当然上述的代码效率不是很高，我们可以使用两个数组来进行维护。

    public List<Integer> largestDivisibleSubset(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if (nums.length == 0) return res;
        Arrays.sort(nums);
        int[] dp = new int[nums.length];
        int[] prev = new int[nums.length];
        int max = 0;
        int index = -1;
        for (int i = 0; i < nums.length; i++) {
            prev[i] = -1;
            dp[i] = 1;
            for (int j = 0; j < i; j++) {
                if (nums[i] % nums[j] == 0 && dp[j] + 1 > dp[i]) {
                    dp[i] = dp[j] + 1;
                    prev[i] = j;
                }
            }
            if (dp[i] > max) {
                max = dp[i];
                index = i;
            }
        }
        while (index != -1) {
            res.add(nums[index]);
            index = prev[index];
        }
        return res;
    }