UVA1354-Mobile Computing(二进制枚举子集)

Posted 2021-01-01 npugen

Problem UVA1354-Mobile Computing

Accept：267  Submit：2232

Time Limit: 3000 mSec

 Problem Description

 

 

 

 

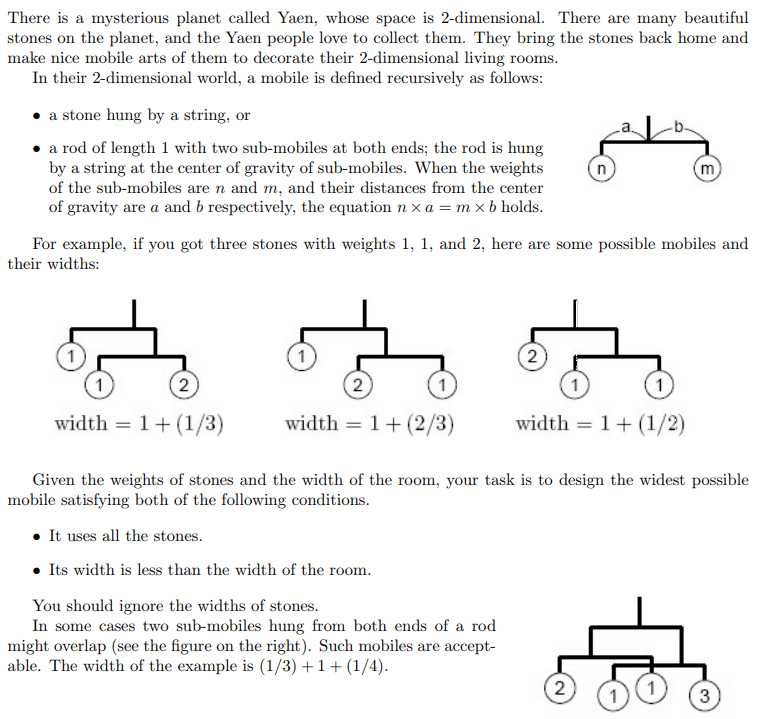
 Input

 

 

 

 Output

 

 

 Sample Input

5

1.3 3

1 2 1

1.4 3

1 2 1

2.0 3

1 2 1

1.59 4

2 1 1 3

1.7143 4

1 2 3 5

 

 Sample Ouput

-1

1.3333333333333335

1.6666666666666667

1.5833333333333335

1.7142857142857142

 

题解：感觉这个题挺难的。把一个天平看作一棵树，叶子节点是砝码，当确定了这棵树的形状及叶子节点的值之后这个天平的长度就是确定的，思路就来自于此。

下面的事情就是枚举子集，以我目前的能力实现起来确实有困难，参考了lrj的代码，这种二进制枚举子集的方式值得学习。

P.S.0有可能是合法输出，而我一开始设Max = 0.0,当没有更新时输出-1，WAWAWAWAWA......

 

 1 #include <bits/stdc++.h>
 2 #define INF 0x3f3f3f3f
 3 using namespace std;
 4 
 5 const int maxn = 6;
 6 int n;
 7 double r,sum[1<<maxn];
 8 double w[maxn];
 9 
10 struct Tree{
11     double L,R;
12     Tree(double L = 0.0,double R = 0.0) :
13         L(L),R(R) {}
14 };
15 
16 vector< vector<Tree> > tree(1<<maxn);
17 bool vis[1<<maxn];
18 
19 void dfs(int subset){
20     if(vis[subset]) return;
21     vis[subset] = true;
22     bool have_child = false;
23     for(int left = (subset-1)&subset;left;left = (left-1)&subset){
24         have_child = true;
25         int right = subset^left;
26         double d1 = sum[right]/sum[subset],d2 = sum[left]/sum[subset];
27         dfs(left),dfs(right);
28         for(int i = 0;i < tree[left].size();i++){
29             for(int j =0;j < tree[right].size();j++){
30                 Tree t;
31                 t.L = max(tree[left][i].L+d1,tree[right][j].L-d2);
32                 t.R = max(tree[right][j].R+d2,tree[left][i].R-d1);
33                 if(t.R+t.L < r) tree[subset].push_back(t);
34             }
35         }
36     }
37     if(!have_child) tree[subset].push_back(Tree());
38 }
39 
40 int main()
41 {
42     //freopen("input.txt","r",stdin);
43     //freopen("output.txt","w",stdout);
44     int iCase;
45     scanf("%d",&iCase);
46     while(iCase--){
47         scanf("%lf%d",&r,&n);
48         for(int i = 0;i < n;i++){
49             scanf("%lf",&w[i]);
50         }
51         memset(vis,false,sizeof(vis));
52         for(int i = 0;i < (1<<n);i++){
53             sum[i] = 0.0;
54             tree[i].clear();
55             for(int j = 0;j < n;j++){
56                 if(i&(1<<j)) sum[i] += w[j];
57             }
58         }
59         int root = (1<<n)-1;
60         dfs(root);
61         double Max = -1;
62         for(int i = 0;i < tree[root].size();i++){
63             Max = max(Max,tree[root][i].L+tree[root][i].R);
64         }
65         printf("%.10lf
",Max);
66     }
67     return 0;
68 }