[树的直径] SDOI2013 直径

Posted 2020-12-31 real-l

SDOI2013 直径

题目描述

小Q最近学习了一些图论知识。根据课本，有如下定义。树：无回路且连通的无向图，每条边都有正整数的权值来表示其长度。如果一棵树有N个节点，可以证明其有且仅有N-1 条边。

路径：一棵树上，任意两个节点之间最多有一条简单路径。我们用 dis(a,b)表示点a和点b的路径上各边长度之和。称dis(a,b)为a、b两个节点间的距离。

直径：一棵树上，最长的路径为树的直径。树的直径可能不是唯一的。

现在小Q想知道，对于给定的一棵树，其直径的长度是多少，以及有多少条边满足所有的直径都经过该边。

输入输出格式

输入格式：

第一行包含一个整数N，表示节点数。 接下来N-1行，每行三个整数a, b, c ，表示点 a和点b之间有一条长度为c的无向边。

输出格式：

共两行。第一行一个整数，表示直径的长度。第二行一个整数，表示被所有直径经过的边的数量。

输入输出样例

输入样例#1：

6
3 1 1000
1 4 10
4 2 100
4 5 50
4 6 100

输出样例#1：

1110
2

说明

【样例说明】 直径共有两条，3 到2的路径和3到6的路径。这两条直径都经过边(3, 1)和边(1, 4)。

对于100%的测试数据：2<=N<=200000，所有点的编号都在1..N的范围内，边的权值<=10^9。

题解

题目传送门:SDOI2013
这道题思路不难,代码也简单(真的不是一般的难调)
讲一下思路吧,

对于第一问,两遍dfs/bfs/dp就出来了,但是由于我们后面还需要用到直径这条路径,所以用dfs/bfs比较好

第二问
如何判断一条边是否是直径上的必须边
我们知道,树的直径长度只有一个,但不只一条
设一条直径上一个点u,我们发现若以u为根的子树,不包括直径上的节点,离它最远的点距离与直径上的端点离它的距离一样,这说明有另一条直径
首先,我们看下面一幅图

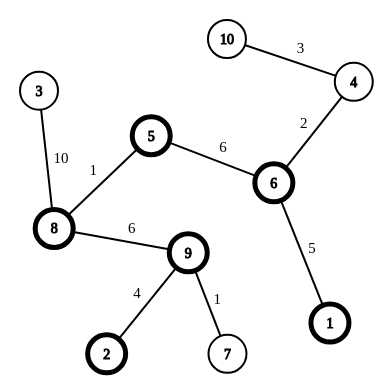
可以看到2-9-8-5-6-1是它的一条直径
但是仔细观察就可以发现,它不只这一条直径

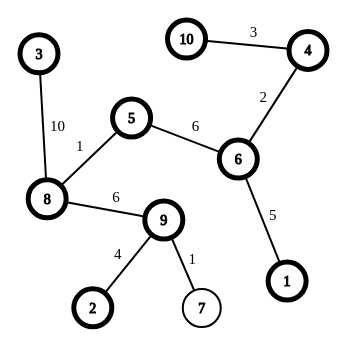
我们看到上面这幅图,3-5-6-1或者是3-5-6-4-10也是一条

所以我们可以保存直径的两个端点,然后左端点向右跳,右端点向左跳,看着条路径上有没有满足上述条件的点,如果有,就把左短点/右端点移到这个点

Code

#include<bits/stdc++.h>
#define rg register
#define Min(a,b) (a)<(b)?(a):(b)
#define Max(a,b) (a)>(b)?(a):(b)

using namespace std;
typedef long long lol;

const int N=200010;

void in(int &ans)
{
  ans=0;int f=1;char i=getchar();
  while(i<'0' || i>'9') {if(i=='-') f=-1;i=getchar();}
  while(i>='0' && i<='9') ans=(ans<<1)+(ans<<3)+(i^48),i=getchar();
  ans*=f;
}

int n,m,cnt,u,v,ans,B;
int nex[N<<1],to[N<<1],head[N],w[N<<1];
int son[N],vis[N],fa[N],dep[N];
lol dis[N],f[N];

inline void add(int a,int b,int c)
{
  to[++cnt]=b,nex[cnt]=head[a];
  w[cnt]=c,head[a]=cnt;
}

void dfs(int u)
{
  for(int i=head[u];i;i=nex[i])
    if(to[i]!=fa[u])
      fa[to[i]]=u, dep[to[i]]=dep[u]+1,dis[to[i]]=dis[u]+w[i], dfs(to[i]);
}

void find(int u)
{
  f[u]=dis[u];
  for(int i=head[u];i;i=nex[i])
    if(!vis[to[i]] && to[i]!=fa[u])
      find(to[i]),f[u]=Max(f[u],f[to[i]]);
}

void Pre()
{
  int x=fa[v];
  while(x) {
    find(x);
    if(f[x]==dis[B]) v=x;
    x=fa[x];
  }
}

void Next()
{
  int x=son[u];
  while(x) {
    find(x);
    if(f[x]-dis[x]==dis[x]) u=x;
    x=son[x];
  }
}

void init()
{
  dfs(1);
  for(int i=1;i<=n;i++) if(dis[i]>dis[u]) u=i;
  memset(dep,0,sizeof(dep));
  memset(fa,0,sizeof(fa));
  memset(dis,0,sizeof(dis));
  dfs(u);
  for(int i=1;i<=n;i++) if(dis[i]>dis[v]) B=v=i;
  printf("%lld
",dis[v]);
  int x=v; while(x) vis[x]=1,son[fa[x]]=x,x=fa[x];
}

int main()
{
  int a,b,c;in(n);
  for(int i=1;i<n;i++) {
    in(a),in(b),in(c);
    add(a,b,c),add(b,a,c);
  }
  init(); Next(); Pre();
  printf("%d
",dep[v]-dep[u]);
}

博主蒟蒻,随意转载.但必须附上原文链接

http://www.cnblogs.com/real-l/