母函数及其应用

Posted 2020-12-30 aininot260

把离散数列和幂级数一 一对应起来

把离散数列间的相互结合关系对应成为幂级数间的运算关系

最后由幂级数形式来确定离散数列的构造

以上三句话是dalao总结的精髓

然后介绍一下定义：

对于任意数列

  

即用如下方法与一个函数联系起来：

则称G(x)是数列的生成函数

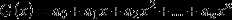
为了便于理解这个东西，下面给出几种典型应用：

使用母函数求出斐波那契数列的通项公式

斐波那契数列的生成函数：

G(x)=x+x2+2x3+3x4+5x5+8x6...

等式两边同时*x有：

xG(x)=x2+x3+2x4+3x5+5x6+8x7+...

相加有：G(x)+xG(x)=x+2x2+3x3+5x4+8x5+13x6+...

G(x)+xG(x)=G(x)/x-1

所以我们可以得到:G(x)=x/(1-x-x2)

然后用数学方法可以求得：

Fib(n)=1/√5[bn+1-an+1]

若有1克、2克、3克、4克的砝码各一 枚，能称出哪几种重量？各有几种可能方案？

用x的指数表示称出的重量

1个1克的砝码可以用函数1+x表示

(前面的这个1表示1克的砝码个数为0)

1个2克的砝码可以用函数1+x^2表示

1个3克的砝码可以用函数1+x^3表示

1个4克的砝码可以用函数1+x^4表示

那么几种砝码的组合情况的用乘积表示有

(1+x)(1+x^2)(1+x^3)(1+x^4)

=1+x+x^2+2x^3+2x^4+2x^5+2x^6+2x^7+x^8+x^9+x^10

系数即为方案数

求用1分、2分、3分的邮票贴出不同数值的方案数？

邮票可以重复

G(x)=(1+x+x^2+....)(1+x^2+x^4+....)(1+x^3+x^6+...)

展开之后的系数就是方案数了

重为a1,a2,a3.....ak的砝码，如何放在天平的两端，求可称重量为n的物体的不同方式

记可称重量为n的物体的不同方式为Cn

它的母函数为：

G(x)=(x^(-a1)+1+x^a1)(x^(-a2)+1+x^a2).........(x^(-ak)+1+x^ak)

x^(-a1)表示砝码a1和物体放在同一个托盘内

x^a1表示砝码和物体放在不同的托盘内

1则为不用这个砝码

重为a1,a2,a3....ak的砝码，如只可以放在天平的一端，求可称重量为n的物体的不同方式

记可称重量为n的物体的不同方式为Cn

G(x)=(1+x^a1)(1+x^a2).........(1+x^ak)

数的划分，将整数分解为若干个整数

假设1出现的次数为记为a1,2出现的次数记为a2.........k出现的次数记为ak

G(x)=(1+x+x^2+x^3+x^4+.....)
(1+x^2+x^4+x^6+x^8+......)
(1+x^3+x^6+x^9+....)
........
(1+xn)

1+x^2+x^4+x^6+x^8的意思是：

当出现一个2时为x^2，当出现两个2时为x^4

数的划分问题在算系数的时候往往结合五边形数定理，具体见上一篇博文

典型例题是HDU1085，给你cnt1个一元硬币，cnt2个两元硬币，cnt3个五元硬币，问不能凑出来的第一个面额是多少

公式为 

(1+x+x^2+x^3+.........x^cnt1)?(1+x^2+x^4+x^6+.........x^cnt2)?(1+x^5+x^10+x^15+............x^cnt5)

处理完了之后这道题就变成了一道模拟题

 1 #include<cstdio>
 2 #include<cstring>
 3 const int maxn=1e4+5;
 4 int mmax;
 5 int c1[maxn],c2[maxn];
 6 int cnt[5],val[5]={1,2,5};
 7 int main()
 8 {
 9     while(scanf("%d%d%d",&cnt[0],&cnt[1],&cnt[2])==3&&(cnt[0]||cnt[1]||cnt[2]))
10     {
11         memset(c1,0,sizeof(c1));
12         memset(c2,0,sizeof(c2));
13         mmax=0;
14         for(int i=0;i<3;i++)
15             mmax+=cnt[i]*val[i];
16         for(int i=0;i<=cnt[0];i++) c1[i]=1;
17         for(int i=1;i<3;i++)
18         {
19             for(int j=0;j<=mmax;j++)
20             {
21                 if(c1[j]!=0)
22                 {
23                     for(int k=0;k<=val[i]*cnt[i];k+=val[i])
24                     {
25                         if(j+k<=mmax) c2[j+k]+=c1[j];
26                     }
27                 }
28             }
29             memcpy(c1,c2,sizeof(c1));
30             memset(c2,0,sizeof(c2));
31         }
32         int i;
33         for(i=0;i<=mmax;i++)
34             if(c1[i]==0) break;
35         printf("%d
",i);
36     }
37     return 0;
38 }