随机过程11 - 泊松过程及其解析计算
Posted Ciaran-byte
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了随机过程11 - 泊松过程及其解析计算相关的知识,希望对你有一定的参考价值。
泊松过程定义及其解析计算
文章目录
1. 课程回顾与概述
随机过程可以根据时间的连续与否和状态的连续与否分为四个大类。其中,高斯过程是一种连续时间,连续状态的随机过程,也是我们之前学习的重点。对连续时间,连续状态的随机过程,我们研究的主要工具是矩,因此,我们从相关的角度考察了高斯过程,事实上,高斯过程仅仅依赖于一阶矩和二阶矩。而时域上的相关,放到频域上就是功率谱。
Continuous Time Discrete State \\textContinuous Time Discrete State Continuous Time Discrete State
接下来,我们会花一些时间了解一下泊松过程。泊松过程是一种连续时间,离散状态的随机过程。对于这种随机过程,由于其相关函数完全没有宽平稳性可言,因此,更多的,我们是从联合分布的角度来研究泊松过程。联合分布是研究泊松过程的主要工具。
Joint Probability \\textJoint Probability Joint Probability
2. 泊松过程的解析计算
2.1 点过程模型建立
点过程就是一种连续时间离散状态的随机过程。我们可以对这个随机过程做某些具象化的描述,比如我们在研究计算机网络的时候,每隔一段时间,就会从其他地方发送过来一组报文;比如我们在研究报销的时候,每隔一段时间会有人来买报销或者要求索赔。
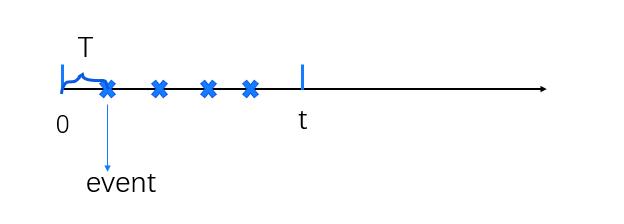
针对这些具体的问题,我们可以把这个模型给抽象出来,就是我们假设每隔时间T会发生一个事件,然后现在我们想统计在时间间隔[s,t]内事件发生的次数。
N ( [ s , t ] ) Number of Events N([s,t]) \\\\ \\textNumber of Events N([s,t])Number of Events
如果说,这些事件发生的时间间隔是确定的,那么在[s,t]时间内发生的次数我们是可以明确计算出来的。用时间段除以时间间隔取整即可。
N ( [ s , t ] ) = [ t − s T ] N([s,t]) = [\\fract-sT] N([s,t])=[Tt−s]
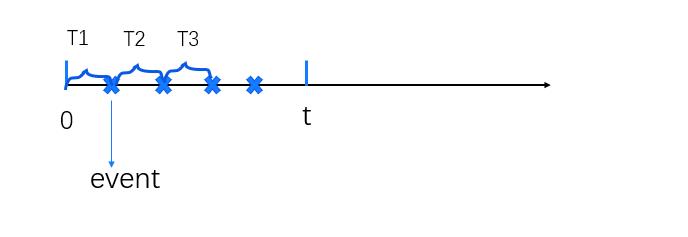
而如果,事件发生的时间间隔是个随机变量,我们依旧想统计时间段t内发生事件的次数,就是一个随机过程了,因为这个次数不但依赖于时间发生的时间间隔,还与时间段的长短有关。N(t)描述的是(0,t)时刻内事件的发生次数。
N
(
t
)
[
0
,
t
]
T
k
:Random Variables
N(t) \\quad [0,t] \\\\ T_k \\text :Random Variables
N(t)[0,t]Tk :Random Variables
这样的随机过程就叫做点过程,也叫做计数过程。
Counting Processes Point Processes \\textCounting Processes \\\\ \\textPoint Processes Counting ProcessesPoint Processes
2.2 泊松过程与点过程
而泊松过程是最简单的点过程。因为泊松过程在点过程的基础上做了一些假设,使得问题变得简单起来。
首先,值得确定的是,初始化状态一定是0。因为零时刻事件发生的次数一定是0
N ( 0 ) = 0 N(0) = 0 N(0)=0
然后,我们来增加三个假设。
(1) Independent Increment ∀ t 1 < t 2 < t 3 < t 4 Z ( t 4 ) − Z ( t 3 ) ⊥ Z ( t 2 ) − Z ( t 1 ) \\text(1) Independent Increment \\\\ \\forall t_1<t_2<t_3< t_4 \\\\ Z(t_4) - Z(t_3) \\perp Z(t_2) - Z(t_1) (1) Independent Increment∀t1<t2<t3<t4Z(t4)−Z(t3)⊥Z(t2)−Z(t1)
第一个假设,这个随机过程具有独立增量特性。
所谓独立增量特性是指,任取四个时刻,可以构成两个时间上没有重叠的增量,这个两个增量彼此之间是独立的。这就意味着前面一段时间事件发生的次数不会影响后面一段时间事件发生的次数。
事实上,实际情况中,独立增量特性并不容易得到满足。比如我们去银行,每个办理业务的人要先取号。如果取号的人很多,后面的人看到大厅中人数很多,并且排队人数很多,取号过大,后面的人很大可能就会选择离开不办理业务了。比如网络数据,处理数据是需要时间的,如果处理数据的时候,又发送来了新的数据,会放进buffer中进行暂存,如果数据量过多过大,buffer会满,如果再来其他数据,就会发生丢包,这个时候网络就会发生拥塞。因此,实际情况中,往往前面事件的发生次数是与后面有关的。
(2) Stationary Increment Z ( t ) − Z ( s ) ∼ P ( t − s ) \\text(2) Stationary Increment \\\\ Z(t) - Z(s) \\sim P(t-s) (2) Stationary IncrementZ(t)−Z(s)∼P(t−s)
第二个假设是,这个随机过程具有平稳增量特性。
一般而言,平稳性是针对不同的统计特性而言的。比如宽平稳是针对相关函数的,相关函数只与两个时刻的时间差有关,而与具体时间没有关系。而平稳增量是针对增量的统计特性,这一段增量是一个离散的随机变量,这个统计特性是这个随机变量的分布,他的统计分布,只依赖于这段时间的长度。
事实上,平稳增量特性在实际情况中叶不容易满足比如网络的繁忙程度与时间有关系,下午三点和晚上三点网络的流量是不同的。
(3) Sparsity \\text(3) Sparsity \\\\ (3) Sparsity
第三个假设是,这个随机过程具有稀疏性,就是若干个事件挤在一起发生的概率比较低。
2.3 泊松过程的概率计算
下面我们要做的事情,是希望基于泊松过程所做的三个假设,对一段时间内事件发生的次数的统计特性进行解析计算。要计算这个统计特性,就是要计算t时刻内事件发生k次的概率
P ( N ( t ) = k ) P(N(t) = k) P(N(t)=k)
2.3.1 母函数
为了得到这个概率的计算,我们需要引入一个工具,这个工具叫做母函数
Moment Generating function \\textMoment Generating function Moment Generating function
母函数的定义是这样的
G x ( Z ) = E ( Z x ) Z ∈ C G x ( Z ) = ∑ k Z k P ( x = k ) G_x(Z) = E(Z^x) \\quad Z \\in\\Complex \\\\ G_x(Z) = \\sum_k Z^k P(x=k) Gx(Z)=E(Zx)Z∈CGx(Z)=k∑ZkP(x=k)
Z - Transform \\textZ - Transform Z - Transform
其中Z是一个复数
我们可以发现母函数和特征函数具有相似性,当复数Z选在单位圆上的时候,其实就是特征函数,特征函数是母函数的一个特例。事实上,特征函数更适合于处理连续时间的分布,因为本质上就是个反傅里叶变换。而母函数更加适合处理离散的随机变量,本质上是个Z变换。
对于泊松分布来说,泊松分布的母函数定义如下
G N ( t ) ( Z ) = E ( Z N ( t ) ) = ∑ k Z k P ( N ( t ) = k ) G_N(t)(Z) = E(Z^N(t)) \\\\ = \\sum_k Z^k P(N(t)=k) GN(t)(Z)=E(ZN(t))=k∑ZkP(N(t)=k)
2.3.2 母函数的求解
(1) 拆分
下面我们想对母函数进行解析计算。我们想从母函数的微分入手
d
G
N
(
t
)
(
Z
)
d
t
=
G
N
(
t
+
Δ
t
)
(
Z
)
−
G
N
(
t
)
(
Z
)
Δ
t
Δ
t
→
0
=
E
(
Z
N
(
t
+
Δ
t
)
)
−
E
(
Z
N
(
t
)
)
Δ
t
=
E
(
Z
N
(
t
+
Δ
t
)
−
Z
N
(
t
)
)
Δ
t
=
E
(
Z
N
(
t
)
(
Z
N
(
t
+
Δ
t
)
−
N
(
t
)
−
1
)
)
Δ
t
=
E
(
Z
N
(
t
)
−
N
(
0
)
(
Z
N
(
t
+
Δ
t
)
−
N
(
t
)
−
1
)
)
Δ
t
\\fracdG_N(t)(Z)dt = \\fracG_N(t+\\Delta t)(Z)-G_N(t)(Z)\\Delta t \\quad \\Delta t \\rightarrow 0\\\\ = \\fracE(Z^N(t+\\Delta t))-E(Z^N(t))\\Delta t = \\fracE(Z^N(t+\\Delta t)-Z^N(t))\\Delta t \\\\ = \\fracE(Z^N(t)(Z^N(t+\\Delta t) - N(t)-1))\\Delta t = \\fracE(Z^N(t) - N(0)(Z^N(t+\\Delta t) - N(t)-1))\\Delta t
dtdGN(t)(Z)=ΔtGN(t+Δt)(Z)−GN(t)(Z)Δt→0=ΔtE(ZN(t+Δt))−E(ZN(t))=ΔtE(ZN(t+Δt)−ZN(t))=ΔtE(ZN(t)(ZN(t+Δt)−N(t)−1))=Δt< 以上是关于随机过程11 - 泊松过程及其解析计算的主要内容,如果未能解决你的问题,请参考以下文章