数据结构图---最小生成树（普里姆算法）

Posted 2020-12-30 ssyfj

一：最小生成树

（一）定义

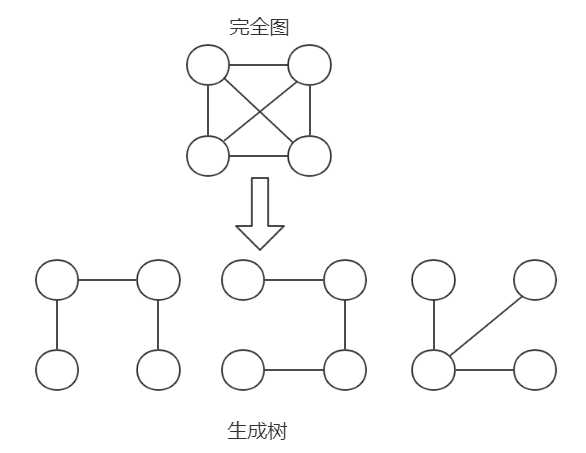
我们把构造连通网的最小代价生成树称为最小生成树

（二）什么是最小生成树？

1.是一棵树

1）无回路
2）N个顶点，一定有N-1条边

2.是生成树

1）包含全部顶点
2）N-1条边都在图中

3.边的权重和最小

（三）案例说明

在实际生活中，我们常常碰到类似这种一类问题:如果要在n个城市之间建立通信联络网，

则连通n个城市仅仅须要n-1条线路。这时。我们须要考虑这样一个问题。怎样在最节省经费前提

下建立这个通信网.换句话说，我们须要在这n个城市中找出一个包括全部城市的连通子图，使得

其全部边的经费之和最小. 这个问题能够转换为一个图论的问题:图中的每一个节点看成是一个城市，

节点之间的无向边表示修建该路的经费。即每条边都有其对应的权值，而我们的目标是挑选n-1条

边使全部节点保持连通。而且要使得经费之和最小.

       这里存在一个显而易见的事实是: 最优解中必定不存在循环(可通过反证法证明). 因此。最后找

出的包括全部城市的连通子图必定没有环路。

这样的连通且没有环路的连通图就简称为树。而在一个

连通图中删除全部的环路而形成的树叫做该图的生成树.对于城市建立通信连通网。须要找出的树由

于具有最小的经费之和。因此又被称为最小生成树(Minimum Cost Spanning Tree)，简称MST.

二：贪心算法

1.什么是贪？

每一步都要最好（只看下一步）

2.什么是好？

权重最小的边

3.需要约束

1.只能用图里有的边
2.只能正好用掉N-1条边
3.不能有回路

三：普里姆算法（稠密图）

（一）定义

对于一个带权的无向连通图，其每个生成树所有边上的权值之和可能不同，我们把所有边上权值之和最小的生成树称为图的最小生成树。
普里姆算法是以其中某一顶点为起点，逐步寻找各个顶点上最小权值的边来构建最小生成树。
其中运用到了回溯，贪心的思想。

 （二）算法思路

设图G=(V,E),U是顶点集V的一个非空子集。假设(u,v)是一条具有最小权值的边。当中u∈U,v∈V-U,

则必存在一棵包括边(u,v)的最小生成树.

上述的性质能够通过反证法证明。假设(u,v)不包括在G的最小生成树T中。那么，T的路径中必定存

在一条连通U和V-U的边，假设将这条边以(u,v)来替换，我们将获得一个权重更低的生成树，这与T

是最小生成树矛盾.既然MST满足贪婪选择属性。那么。求解最小生成树的问题就简化了非常多。

总结一下，详细的步骤大概例如以下：

1.构建一棵空的最小生成树T。并将全部节点赋值为无穷大.
2.任选一个节点放入T。另外一个节点集合为V-T.
3.对V-T中节点的赋值进行更新(因为此时新增加一个节点，这些距离可能发生变化)
4.从V-T中选择赋值最小的节点，增加T中
5.假设V-T非空，继续步骤3～5，否则算法终结

（三）步骤模拟

原图：

 

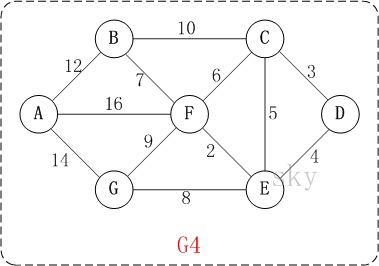
以上图G4为例，来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。

 

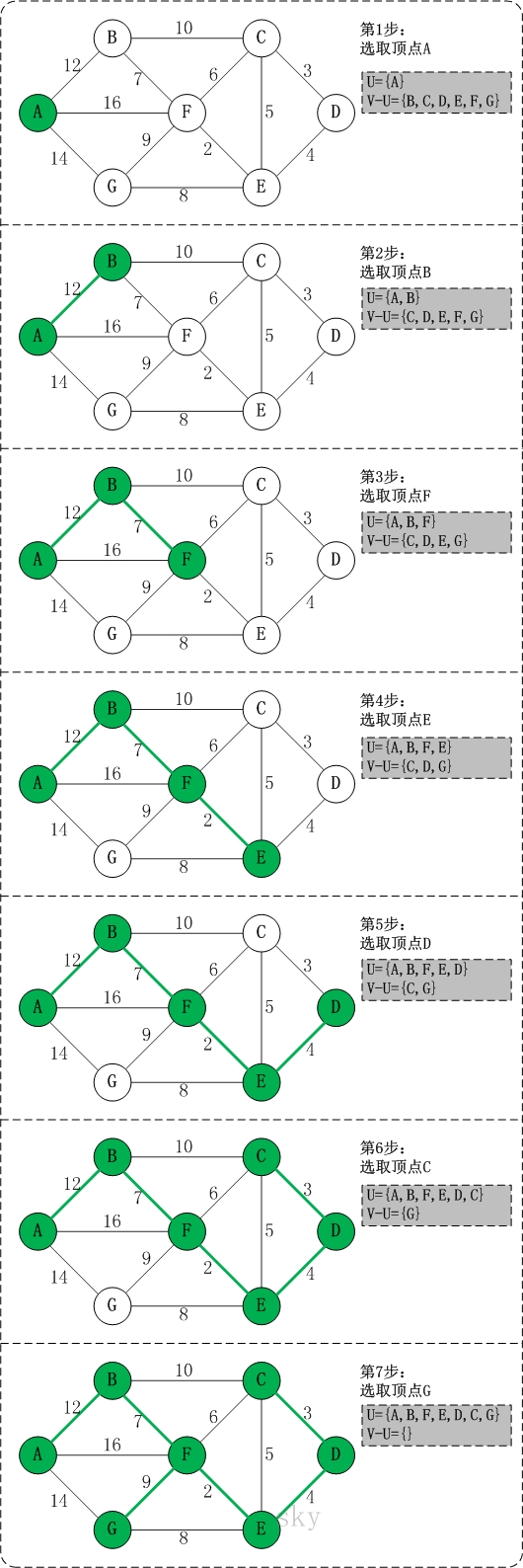
初始状态：V是所有顶点的集合，即V={A,B,C,D,E,F,G}；U和T都是空！ 

第1步：将顶点A加入到U中。 
    此时，U={A}。 
第2步：将顶点B加入到U中。 
    上一步操作之后，U={A}, V-U={B,C,D,E,F,G}；因此，边(A,B)的权值最小。将顶点B添加到U中；此时，U={A,B}。 
第3步：将顶点F加入到U中。 
    上一步操作之后，U={A,B}, V-U={C,D,E,F,G}；因此，边(B,F)的权值最小。将顶点F添加到U中；此时，U={A,B,F}。 
第4步：将顶点E加入到U中。 
    上一步操作之后，U={A,B,F}, V-U={C,D,E,G}；因此，边(F,E)的权值最小。将顶点E添加到U中；此时，U={A,B,F,E}。 
第5步：将顶点D加入到U中。 
    上一步操作之后，U={A,B,F,E}, V-U={C,D,G}；因此，边(E,D)的权值最小。将顶点D添加到U中；此时，U={A,B,F,E,D}。 
第6步：将顶点C加入到U中。 
    上一步操作之后，U={A,B,F,E,D}, V-U={C,G}；因此，边(D,C)的权值最小。将顶点C添加到U中；此时，U={A,B,F,E,D,C}。 
第7步：将顶点G加入到U中。 
    上一步操作之后，U={A,B,F,E,D,C}, V-U={G}；因此，边(F,G)的权值最小。将顶点G添加到U中；此时，U=V。

此时，最小生成树构造完成！它包括的顶点依次是：A B F E D C G。

（三）算法实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>

#define MAXVEX 100    //最大顶点数
#define INFINITY 65535    //用0表示∞

typedef char VertexType;    //顶点类型，字符型A,B,C,D...
typedef int EdgeType;    //边上权值类型10,15,...

//邻接矩阵结构
typedef struct
{
    VertexType vers[MAXVEX];    //顶点表
    EdgeType arc[MAXVEX][MAXVEX];    //邻接矩阵，可看作边表
    int numVertexes, numEdges;    //图中当前的顶点数和边数
}MGraph;


void CreateMGraph(MGraph* G);
void showGraph(MGraph G);

void MiniSpanTree_prim(MGraph G);    //Prim算法生成最小生成树

//Prim算法生成最小生成树
void MiniSpanTree_prim(MGraph G)
{
    int min, i, j, k;
    int adjvex[MAXVEX];        //保存相关顶点下标
    int lowcost[MAXVEX];    //保存相关顶点间边的权值
    lowcost[0] = 0;    //初始化第一个权值为0，即将v0加入生成树
    //lowcost的值为0表示此下标的顶点已经加入生成树
    adjvex[0] = 0;    //初始化第一个顶点下标为0
    for (i = 1; i < G.numVertexes;i++)
    {
        lowcost[i] = G.arc[0][i];    //将v0顶点与之有关的边的权值都存放入权值数组
        adjvex[i] = 0;    //初始化都为v0的下标
    }

    for (i = 1; i < G.numVertexes;i++)
    {
        min = INFINITY;
        j = 1;
        k = 0;
        while (j<G.numVertexes)
        {
            if (lowcost[j]!=0&&lowcost[j]<min)
            {
                //如果权值不为0且权值小于min
                min = lowcost[j];    //则让当前权值成为最小值
                k = j;    //将当前最小值的下标存放k
            }
            j++;
        }
        printf("(%d,%d)", adjvex[k], k);    //打印当前顶点边中权值最小边
        lowcost[k] = 0;//将当前顶点的权值置为0，表示此顶点已经完成任务

        //和上面做了几乎一样的操作，就是更新权值
        for (j = 1; j < G.numVertexes;j++)    //循环所有顶点，因为我们已经确认第一个放入的0，所有我们循环可以省去0
        {
            if (lowcost[j] != 0 && G.arc[k][j]<lowcost[j])    
            {//若下标为k顶点个边权值小于此前顶点，就不会加入生成树权值
                lowcost[j] = G.arc[k][j];    //将较小权值存入lowcost
                adjvex[j] = k;        //将下标为k的顶点存入adjvex
            }
        }
    }
}

int main()
{
    MGraph MG;
    CreateMGraph(&MG);
    showGraph(MG);
    MiniSpanTree_prim(MG);
    system("pause");
    return 0;
}

void CreateMGraph(MGraph* G)
{
    int i, j, k, w;
    G->numVertexes = 9;
    G->numEdges = 15;
    //读入顶点信息
    G->vers[0] = ‘A‘;
    G->vers[1] = ‘B‘;
    G->vers[2] = ‘C‘;
    G->vers[3] = ‘D‘;
    G->vers[4] = ‘E‘;
    G->vers[5] = ‘F‘;
    G->vers[6] = ‘G‘;
    G->vers[7] = ‘H‘;
    G->vers[8] = ‘I‘;

    //getchar();    //可以获取回车符
    for (i = 0; i < G->numVertexes; i++)
        for (j = 0; j < G->numVertexes; j++)
            G->arc[i][j] = INFINITY;    //邻接矩阵初始化

    G->arc[0][1] = 10;
    G->arc[0][5] = 11;
    G->arc[1][2] = 18;
    G->arc[1][6] = 16;
    G->arc[1][8] = 12;
    G->arc[2][3] = 22;
    G->arc[2][8] = 8;
    G->arc[3][4] = 20;
    G->arc[3][7] = 16;
    G->arc[3][6] = 24;
    G->arc[3][8] = 21;
    G->arc[4][5] = 26;
    G->arc[4][7] = 7;
    G->arc[5][6] = 17;
    G->arc[6][7] = 19;

    for (k = 0; k < G->numVertexes; k++)    //读入numEdges条边，建立邻接矩阵
    {
        for (i = k; i < G->numVertexes; i++)
        {
            G->arc[i][k] = G->arc[k][i];    //因为是无向图，所有是对称矩阵
        }
    }
}



void showGraph(MGraph G)
{
    for (int i = 0; i < G.numVertexes; i++)
    {
        for (int j = 0; j < G.numVertexes; j++)
        {
            if (G.arc[i][j] != INFINITY)
                printf("%5d", G.arc[i][j]);
            else
                printf("    0");
        }
        printf("
");
    }
}

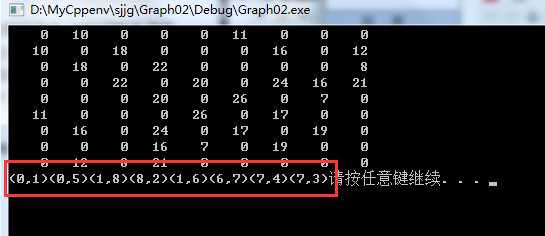
（四）普里姆代码分析

//Prim算法生成最小生成树
void MiniSpanTree_prim(MGraph G)
{
    int min, i, j, k;
    int adjvex[MAXVEX];        //保存相关顶点下标
    int lowcost[MAXVEX];    //保存相关顶点间边的权值
    lowcost[0] = 0;    //初始化第一个权值为0，即将v0加入生成树
    //lowcost的值为0表示此下标的顶点已经加入生成树
    adjvex[0] = 0;    //初始化第一个顶点下标为0
    for (i = 1; i < G.numVertexes;i++)
    {
        lowcost[i] = G.arc[0][i];    //将v0顶点与之有关的边的权值都存放入权值数组
        adjvex[i] = 0;    //初始化都为v0的下标
    }

    for (i = 1; i < G.numVertexes;i++)
    {
        min = INFINITY;
        j = 1;
        k = 0;
        while (j<G.numVertexes)
        {
            if (lowcost[j]!=0&&lowcost[j]<min)
            {
                //如果权值不为0且权值小于min
                min = lowcost[j];    //则让当前权值成为最小值
                k = j;    //将当前最小值的下标存放k
            }
            j++;
        }
        printf("(%d,%d)", adjvex[k], k);    //打印当前顶点边中权值最小边
        lowcost[k] = 0;//将当前顶点的权值置为0，表示此顶点已经完成任务

        //和上面做了几乎一样的操作，就是更新权值
        for (j = 1; j < G.numVertexes;j++)    //循环所有顶点，因为我们已经确认第一个放入的0，所有我们循环可以省去0
        {
            if (lowcost[j] != 0 && G.arc[k][j]<lowcost[j])    
            {//若下标为k顶点个边权值小于此前顶点，就不会加入生成树权值
                lowcost[j] = G.arc[k][j];    //将较小权值存入lowcost
                adjvex[j] = k;        //将下标为k的顶点存入adjvex
            }
        }
    }
}

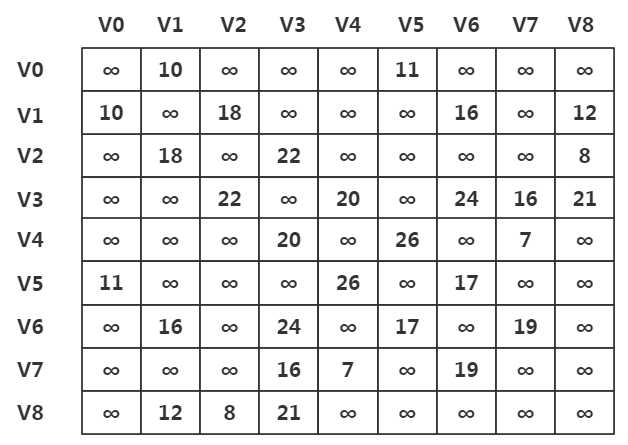
下面是我们要处理的邻接矩阵

1.创建两个数组，一个存放顶点，一个存放相关顶点间边的权值

int adjvex[MAXVEX];        //保存相关顶点下标
int lowcost[MAXVEX];    //保存相关顶点间边的权值

作用：

adjvex数组：将存放我们左侧的顶点下标
lowcost数组：将存放我们对应顶点的各个边的权值

会利用这两个来打印出我们所需要的最小边

printf("(%d,%d)", adjvex[k], k); //打印当前顶点边中权值最小边   

其中adjvex[k]存放的是我们左侧的弧尾，k是我们找的的邻接点权值最小的弧头

注意：

比如我们要找v3顶点作为弧头的边，那么我们adjvex[3]中将会存放其弧尾，也就是我们的左侧下标

那么我们去找第一条边时，我们只知道与v0相邻顶点间边的权值，并不知道k值，所以我们开始无法知道adjvex[k]=0中k是谁。
但是我们可以在开始对顶点数组adjvex进行初始化，全部初始化为0，就可以解决这个问题

    lowcost[0] = 0;    //初始化第一个权值为0，即将v0加入生成树
    //lowcost的值为0表示此下标的顶点已经加入生成树
    adjvex[0] = 0;    //初始化第一个顶点下标为0
    for (i = 1; i < G.numVertexes;i++)
    {
        lowcost[i] = G.arc[0][i];    //将v0顶点与之有关的边的权值都存放入权值数组
        adjvex[i] = 0;    //初始化都为v0的下标
    }

其中lowcost[0] = 0;是因为我们开始就将v0点放入生成树中，所以要将对应的lowcost[0]设置为0，我们会在后面，将所有的放入生成树中的顶点全部设置为0，但是注意生成树在代码中不是直接出现的

其中lowcost[i] = G.arc[0][i];  是将对应的邻接顶点的权值放入lowcost中

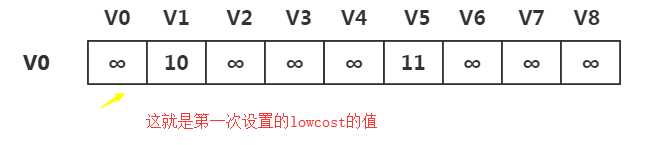
2.循环所有的左侧顶点，获取他们相关的最小邻接边

    for (i = 1; i < G.numVertexes;i++)
    {
        min = INFINITY;
        j = 1;
        k = 0;
        while (j<G.numVertexes)
        {
            if (lowcost[j]!=0&&lowcost[j]<min)
            {
                //如果权值不为0且权值小于min
                min = lowcost[j];    //则让当前权值成为最小值
                k = j;    //将当前最小值的下标存放k
            }
            j++;
        }
        printf("(%d,%d)", adjvex[k], k);    //打印当前顶点边中权值最小边
        lowcost[k] = 0;//将当前顶点的权值置为0，表示此顶点已经完成任务

        //和上面做了几乎一样的操作，就是更新权值
        for (j = 1; j < G.numVertexes;j++)    //循环所有顶点，因为我们已经确认第一个放入的0，所有我们循环可以省去0
        {
            if (lowcost[j] != 0 && G.arc[k][j]<lowcost[j])    
            {//若下标为k顶点个边权值小于此前顶点，就不会加入生成树权值
                lowcost[j] = G.arc[k][j];    //将较小权值存入lowcost
                adjvex[j] = k;        //将下标为k的顶点存入adjvex
            }
        }
    }

其中while循环是获取我们的权值中最小的那个的弧头下标，将会和弧尾组成一条边：

        while (j<G.numVertexes)
        {
            if (lowcost[j]!=0&&lowcost[j]<min)
            {
                //如果权值不为0且权值小于min
                min = lowcost[j];    //则让当前权值成为最小值
                k = j;    //将当前最小值的下标存放k
            }
            j++;
        }

下面的权值都会存在lowcost中

　          

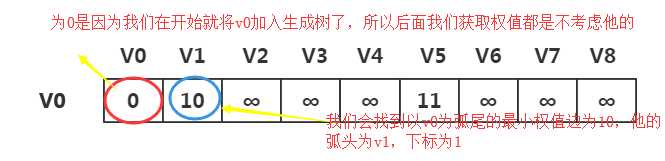
　　　　printf("(%d,%d)", adjvex[k], k);　　//可以打印处这条边

我们将找到的这个顶点和上面初始时设置的lowcost一样设置为0，表示已经加入生成树，我们不必去修改他们

　　　　lowcost[k] = 0;//将当前顶点的权值置为0，表示此顶点已经完成任务

下面的for循环和我们之前的for循环更新权值是一致的，但是有些不同

        //和上面做了几乎一样的操作，就是更新权值
        for (j = 1; j < G.numVertexes;j++)    //循环所有顶点，因为我们已经确认第一个放入的0，所有我们循环可以省去0
        {
            if (lowcost[j] != 0 && G.arc[k][j]<lowcost[j])    
            {//若下标为k顶点个边权值小于此前顶点，就不会加入生成树权值
                lowcost[j] = G.arc[k][j];    //将较小权值存入lowcost
                adjvex[j] = k;        //将下标为k的顶点存入adjvex
            }
        }

首先我们做了比较

if (lowcost[j] != 0 && G.arc[k][j]<lowcost[j])   

首先顶点不能及时生成树中的，即lowcost[j]!=0,然后其弧权值需要比原来的权值小才行，因为可能出现原来的权值更加小，这是就要选择原来的边作为新的路径

                lowcost[j] = G.arc[k][j];    //将较小权值存入lowcost
                adjvex[j] = k;        //将下标为k的顶点存入adjvex

我们更新了权值最新值，会在下一次的循环中再次选取下一个点