挑战程序设计竞赛（算法和数据结构）——13.2最小生成树（普里姆）的JAVA实现

Posted 2022-01-02 小乖乖的臭坏坏

题目与讲解思路：

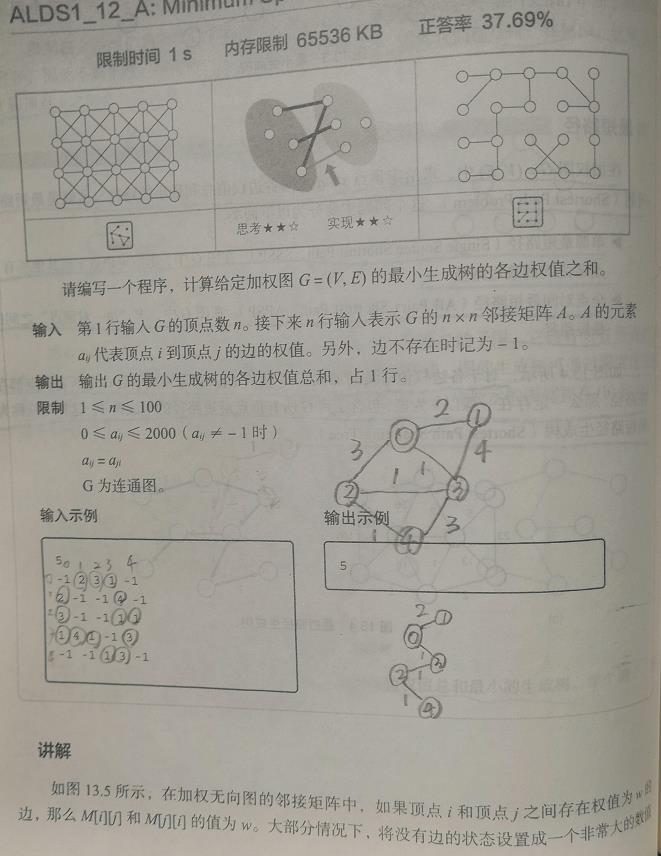
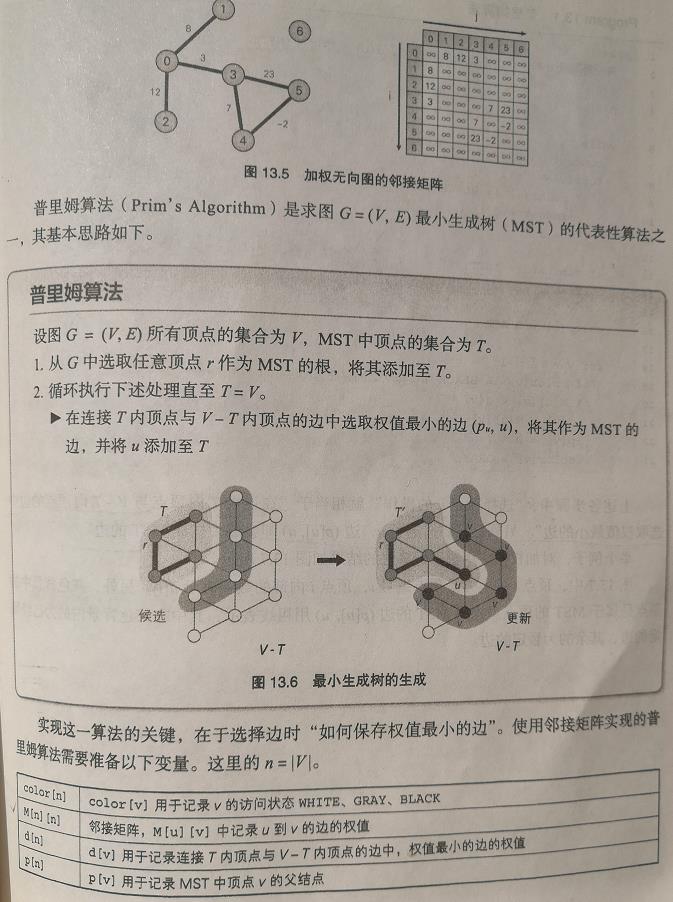
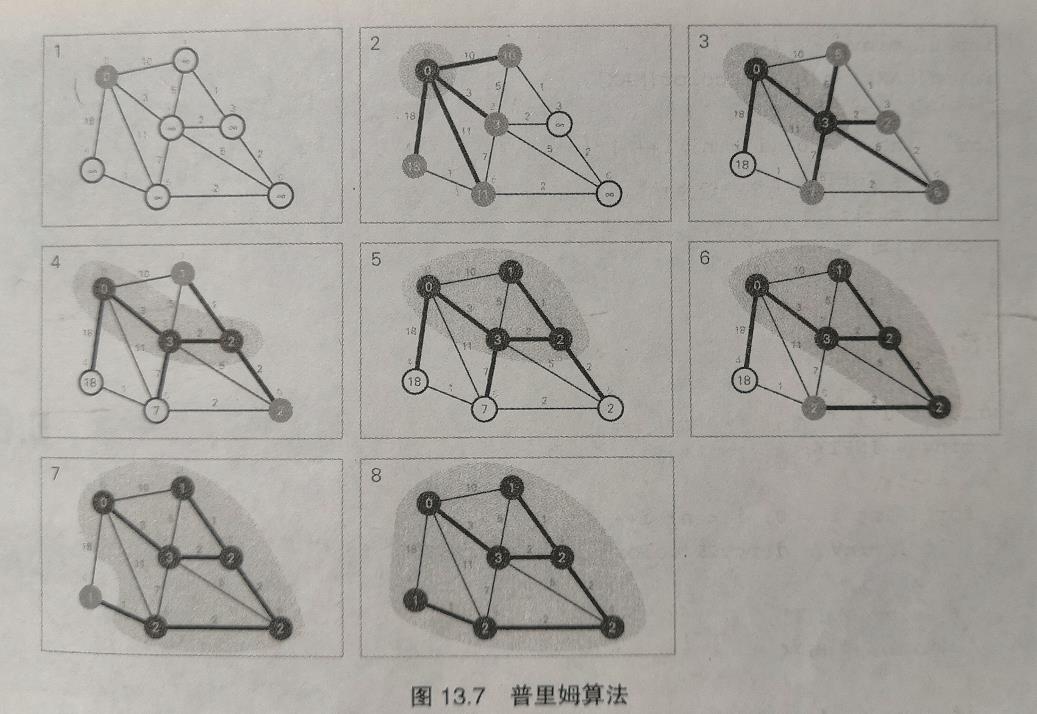
代码：

import java.io.BufferedInputStream;
import java.util.Scanner;

public class MinimumSpanningTree 
    public static void main(String[] args) 
        Scanner cin = new Scanner(new BufferedInputStream(System.in));
        int n = cin.nextInt();
        int M[][] = new int[n][n];
        for (int i=0;i<n;i++)
            for (int j=0;j<n;j++)
                M[i][j] = cin.nextInt();
            
        //完成输入

        String color[] = new String[n];
        int d[] = new int[n];//用于记录连接T内定点与V-T内顶点的边中，权值最小的边的权值
        int p[] = new int[n];//用于记录MST中顶点v的父节点

        int sum = prim(d, p, n, color, M);
        System.out.println(sum);
    

    public static int prim(int d[], int p[], int n, String color[], int M[][])
        int u = -1;
        int sum = 0;

        //将所有顶点u的color[u]设为white，d[u]初始化为Integer.MAXIMUM.
        for (int i=0;i<n;i++)
            color[i] = "white";
            d[i] = Integer.MAX_VALUE;
        

        d[0] = 0;
        p[0] = -1;

        while (true)
            int mincost = Integer.MAX_VALUE;
            for (int i=0;i<n;i++)//对任何一个节点i来讲
                if(!color[i].equals("black") && d[i]<mincost)//只要i还没有内纳入到T中，并且其权值小于mincost
                    mincost = d[i];//那就将其值更新为mincost
                    u = i;//并将其作为当前节点
                
            

            if(mincost==Integer.MAX_VALUE)break;//如果遍历了一圈发现mincost还没有变化，则说明图可能不存在连接，直接跳出即可

            color[u] = "black";//此时将u设置为black，即将u纳入到T中//这行代码以上是寻找到合适的u，以下是将u纳入到体系中并建立一系列连接

            for (int v=0;v<n;v++)
                if(!color[v].equals("black") && M[u][v]!=-1)//只要是和u邻接且未被处理的节点v
                    if(M[u][v]<d[v])//倘若v到T的最小距离比uv之间的距离大，则将v到其中的距离更新，并将u设为v的父节点
                        d[v] = M[u][v];
                        p[v] = u;
                        color[v] = "gray";//将v设为正在处理的状态
                    
                
            
        
        for (int i=0;i<n;i++)
            if(p[i]!=-1)sum += M[i][p[i]];
        
        return sum;
    

输入：

5
-1 2 3 1 -1
2 -1 -1 4 -1
3 -1 -1 1 1
1 4 1 -1 3
-1 -1 1 3 -1

输出：

5