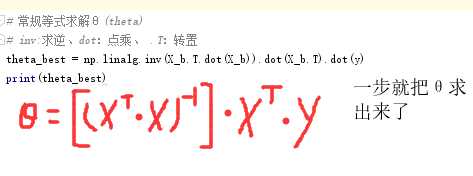机器学习_线性回归

Posted 2020-12-29 yd2018

线性回归

 

人工智能是机器学习的父类；机器学习是深度学习的父类

 

1. 怎么做线性回归？

2. 理解回归 -- 最大似然函数

3. 应用正态分布概率密度函数 -- 对数总似然

4. 推导出损失函数 -- 推导出解析解        

5. 代码实现解析解的方式求解 -- 梯度下降法的开始 -- sklearn模块使用线性回归

 

线性： y = a * x         一次方的变化

回归：回归到平均值

 

简单线性回归

算法 = 公式

 

一元一次方程组

一元：一个x   影响y的因素，维度

一次：x的变化    没有非线性的变化

y = a * x + b

x1,y1        x2,y2        x3,y3        x4,y4 ...

误差最小的 -- 最优解

 

做机器学习，没有完美解，只有最优解

做机器学习就是要以最快的速度，找到误差最小的最优解

 

一个样本的误差：

yi^ - yi

找到误差最小的时刻；为了去找到误差最小的时刻，需要反复尝试，a,b

根据 最小二乘法 去求得误差

反过来误差最小时刻的a,b就是最终最优解模型！！！

 

 

===========================================================================

 

多元线性回归

y = a*x+b

y = w0+w1*x1+w2*x2

向量转置相乘x0=1

不止两个特征

截距(w0)，什么都不做，本身就存在那里(物体本身就漂亮，不加修饰也漂亮)

x1...xn：n个特征

本质上就是算法（公式）变换为了多元一次方程组

y = w1 * x1 + w2 * x2 + w3 * x3 + ... +wn * xn + w0 * x0        (x0恒为1时可不写)

 

 

===========================================================================

 

最大似然估计：

是一种统计方法，用来求一个样本集的相关概率密度函数的参数

‘似然’(likelihood)：即‘可能性’，通俗易懂叫法：‘最大可能性估计’

likelihood 与 probability 同义词

 

 

 

 

中心极限定理：

• 是概率论中讨论 随机变量 序列部分和分步渐进于正态分布的一类定理

 

误差(ε)：

• 第i个样本实际的值 等于 预测的值 加 误差

 

• 假定所有的样本都是独立的，有上下的震荡，震荡认为是随机变量，足够多 的随机变量叠加之后形成的分布，根据中心极限定理，它服从的就是正态分布，因为它是正常状态下的分布

 

最小二乘法：

 

概率密度函数：

最简单的概率密度函数：均匀分布的密度函数，

 

 

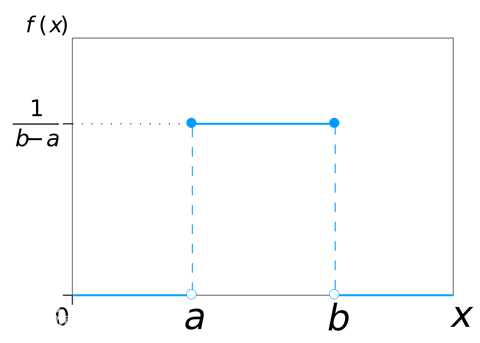
一维正态分布

若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布，且其概率密度函数为

 

 

 

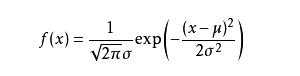
则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布

 

标准正态分布

当μ=0，σ=1时，正态分布就成为标准正态分布：

 

 

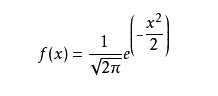
求总似然：

 

 

 

因为连乘太麻烦，故想到用log函数使得连乘变成相加，log函数为单调递增函数，故可以.

 

 

 

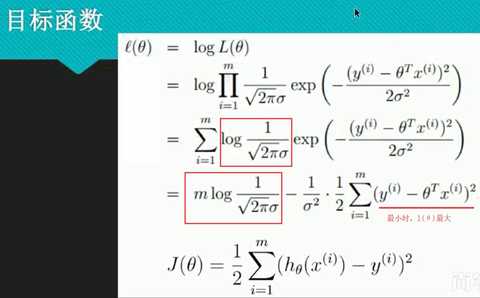
通过最大似然估计的思想，利用了正态分布的概率密度函数，推导出了损失函数

 

误差函数的另一种表达：

 

 

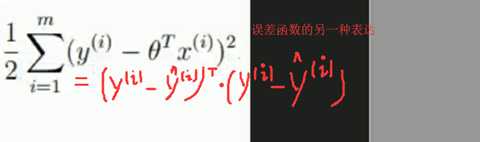
找损失最小的过程就是求极值的过程(导数为0)

 

 

 

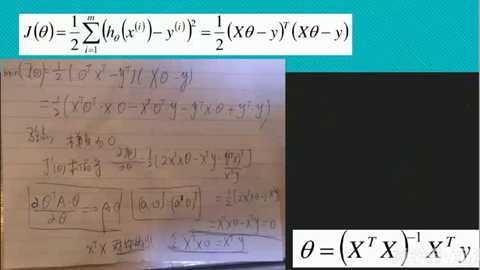
解析解：

 

 

 

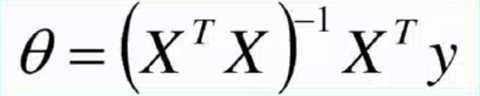
总结：

(1) 为什么求总似然的时候，要用正态分布？

中心极限定理，如果假设样本之间是独立事件，误差变量随即产生，那么就服从正太分布.

 

(2) 总似然不是概率相乘吗？为什么用了概率密度函数的f(xi)进行了相乘？

因为概率不好求，所以当我们可以找到概率密度相乘最大的时候，就相当于找到了概率相乘最大的时候.

 

(3) 概率为什么不好求？

因为求的是面积，需要积分，麻烦。不用去管数学上如何根据概率密度函数去求概率.

 

(4) 总似然最大和最优解有什么关系？

当我们找到可以使得总似然最大的条件，也就是可以找到我们的DataSet数据集最吻合某个正态分布，即找到了最优解

 

通过最大似然估计的思想，利用了正态分布的概率密度函数，推导出了损失函数

 

(5) 什么是损失函数？

一个函数最小，就对应了模型是最优解，预测历史数据可以最准.

 

(6) 线性回归的损失函数是什么？

最小二乘法；MSE(mean squared error)[平方均值损失函数，均方误差]

 

 

(6) 线性回归的损失函数有哪些假设？

样本独立；随机变量；服从正态分布

 

(7) ML学习特点：

不强调模型100%正确；

强调模型是有价值的，堪用的.

 

通过对损失函数求导，来找到最小值，求出θ的最优解；

 

 

代码实现解析解的方式求解

 

import numpy as np
import matplotlib.pyplot as plt
 
#这里相当于是随机X维度X1，rand是随机均匀分布
#rand()：返回0-1之间的数
X=2*np.random.rand(100,1)#100行1列
 
#人为的设置真实的Y一列，np.random.randn(100,1)是设置error(方差)，randn是标准正态分布
#np.random.randn(100,1)返回标准正态分布上的一个随机值，取0的概率比较大一些
#（4+3*X）是预测值、np.random.randn(100,1)是误差ε
#预测值==W的转置*X
#4==W0；3==W1
y=4+3*X+np.random.randn(100,1)#100行1列
 
#整合X0和X1
#np.ones(100,1)输出100行1列个1
X_b=np.c_[np.ones((100,1)),X]
print(X_b)
 
#常规等式求解θ(theta)
#inv:求逆、dot：点乘、.T：转置
theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
 

 

print(theta_best)
 

 

#创建测试集里面的X1
X_new=np.array([[0],[2]])
X_new_b=np.c_[(np.ones((2,1))),X_new]
print(X_new_b)
y_predict=X_new_b.dot(theta_best)
print(y_predict)
‘‘‘
[[3.98173243]
[10.17046616]]
‘‘‘
 

 

 
 
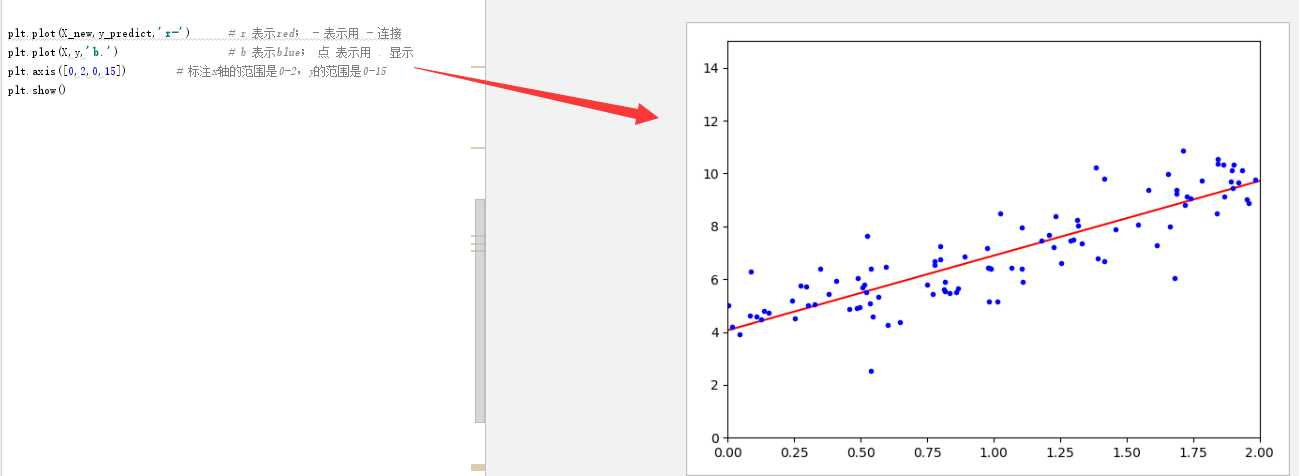
plt.plot(X_new,y_predict,‘r-‘)
plt.plot(X,y,‘b.‘)
plt.axis([0,2,0,15])#标注x轴的范围是0-2，y的范围是0-15
plt.show()
 

 

 
 
实际上当数据特别多的时候，用上述方法求解特别慢