机器学习线性回归

Posted 2022-03-04 宣之于口

线性回归

一、单变量线性回归

1. 假设函数(Hypothesis Function)

因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题: $h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

假设有以下的训练集, 我们假设${\theta }_0=2$ 和 ${\theta }_1=2$, 则假设函数为 $y=2+2x$. 当x=1时, y=4.

2.代价函数(Cost Function)

为模型选择合适的参数${\theta }_0$ 和 ${\theta }_1$。我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数，

使得代价函数最小:$J\left({\theta }_0,{\theta }_1\right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$

代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。求出${\theta }_0$ 和 ${\theta }_1$使得假设函数尽可能多的通过训练集，需要指出的是当$J({\theta }_0,{\theta }_1)=0$时, 我们的假设函数应该通过所有的训练集。

E.G. 我们通过下训练集, 来学习如何计算J(θ)：

• x = 1, y = 1
• x = 2, y = 2
• x = 3, y = 3

当${\theta }_0$=0时: $J({\theta }_0)=\frac{1}{2\ast 3}\ast (1^2+2^2+3^3)=\frac{14}{6}$

3. 梯度下降(Gradient Descent)

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数$J({\theta }_0,{\theta }_1)$ 的最小值。

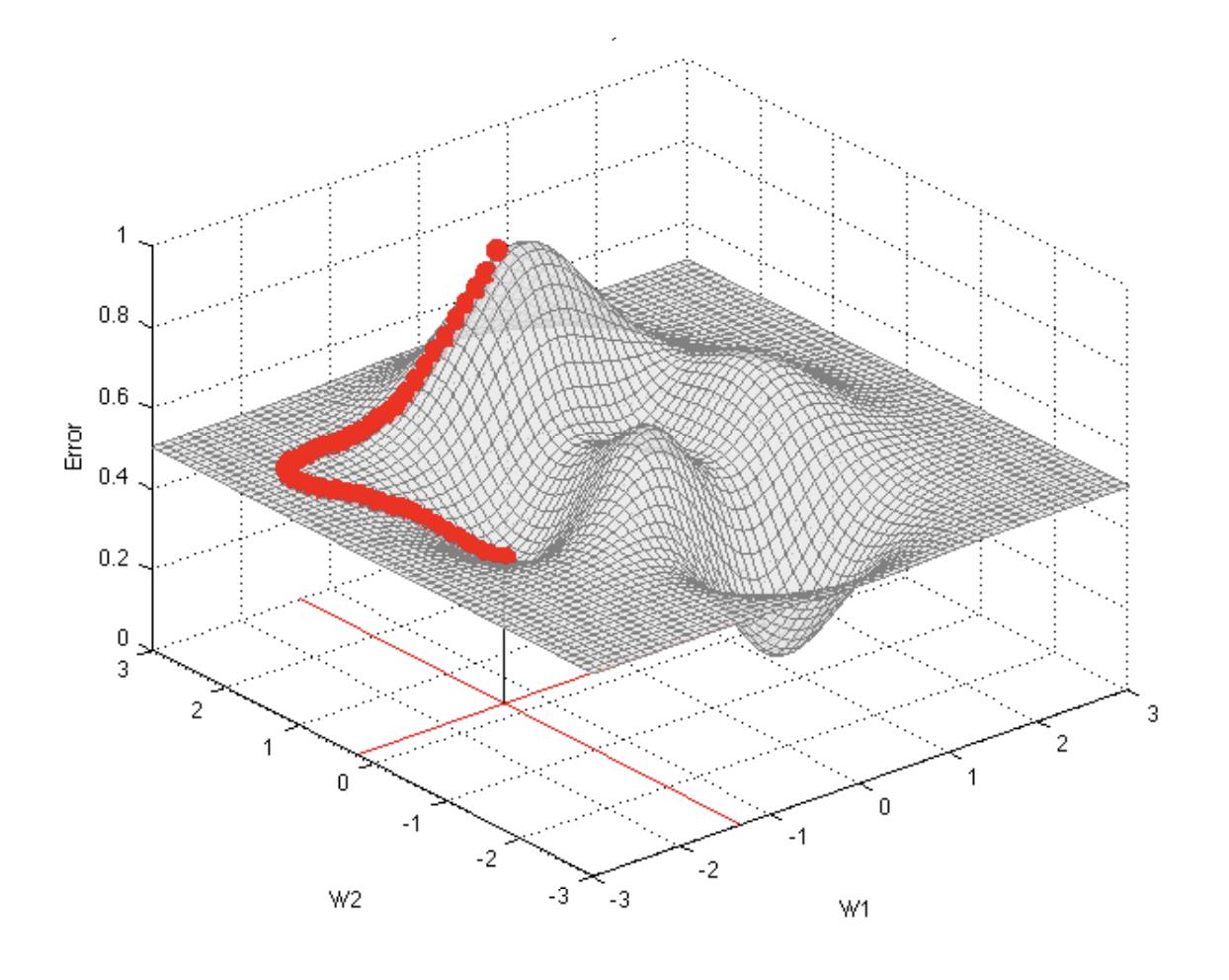
梯度下降背后的思想是：开始时我们随机选择一个参数的组合${\theta }_0,{\theta }_1...{\theta }_n$ ,计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

批量梯度下降公式(batch gradient descent)：${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$

其中α是学习率(learning rate)，它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。由切线可见, 随着斜率的变化，越接近最低点，切线值变化越小。当到达最低点时，切线值接近于0, 得到局部最优解。

同步更新

在梯度下降算法中，需要注意同步更新，即梯度下降中，更新J(θ0)和J(θ1) 时，需要同时更新θ0和θ1

4. 线性回归运用梯度下降

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即: $\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)=\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}{\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$

代入计算可得：${\theta }_0:={\theta }_0-a\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)$ 以及: $以上是关于机器学习线性回归的主要内容，如果未能解决你的问题，请参考以下文章$

python机器学习回归算法-线性回归

机器学习：线性模型学习总结：线性回归

机器学习笔记：梯度下降

如何搞懂机器学习中的线性回归模型？机器学习系列之线性回归基础篇

机器学习-第二节：机器学习模型之线性回归

机器学习-第二节：机器学习模型之线性回归