浅谈树状数组

Posted 2020-12-28 wkfvawl

之前也看过了好多关于树状数组的博客，结合这几天做的题，我一直想好好总结一下树状数组，这篇文章就来浅谈一下树状数组。

 

1.前言

首先我们要明白树状数组是一种数据结构，利用树状数组可以以空间换取时间，这一点和之前的线段树一样，但是树状数组访问会更快，效率更高，树状数组不同于线段数的一点就是这棵树的构成。

二叉树或者线段树是这样的：

 

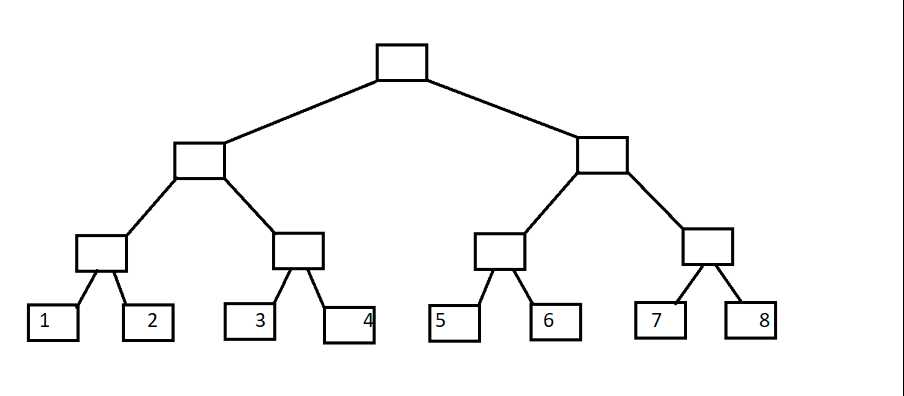
而树状数组是这样的：

 

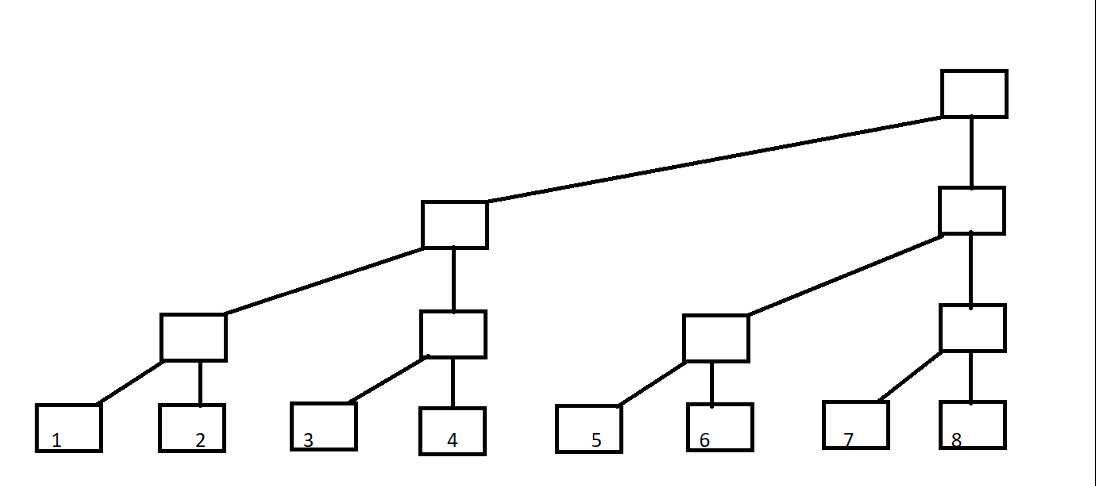
对于树状数组这种数据结构其中有三个数组是非常重要的：

a[ ]数组——被维护的数组，就是这棵树最下面的叶子结点。

c[ ]数组——或许这个才可以真正的称之为树状数组，它是用来存储部分叶子结点之和的，就像是一种工具，就是利用它来提高访问效率的。

sum[ ]数组——前i项a[ ]数组的和，a[ ]的前缀和，这个才是真正需要用来做题的，如何解题全都要围绕这这个sum[ ]数组。

 

2.树状数组的建立

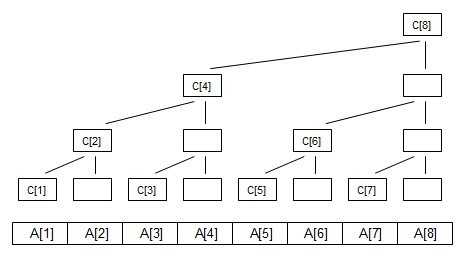
如图可以知道

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

那么这个c[ ]数组到底是怎么样得到的？

 

观察这个图

 

 

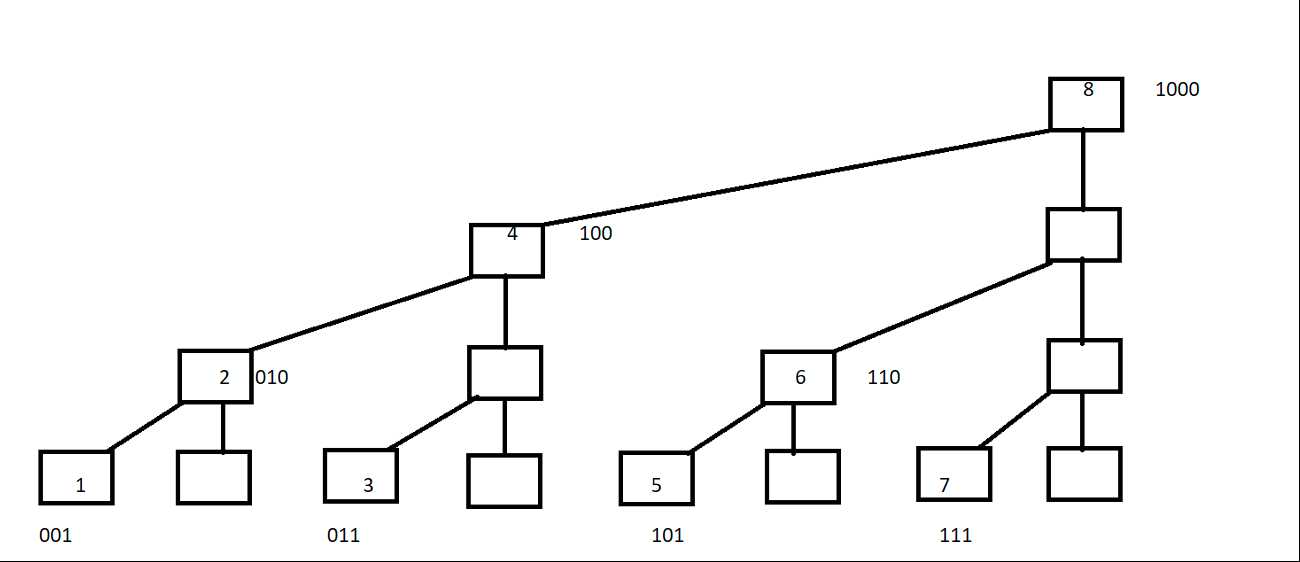
再将其转化为二进制看一下:

 

        C[1] = C[0001] = A[1];

        C[2] = C[0010] = A[1]+A[2];

        C[3] = C[0011] = A[3];

        C[4] = C[0100] = A[1]+A[2]+A[3]+A[4];

        C[5] = C[0101] = A[5];

        C[6] = C[0110] = A[5]+A[6];

        C[7] = C[0111] = A[7];

        C[8] = C[1000] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

 

从上图能看出来每一个数的父节点就是右边比自己末尾零个数多的最近的一个（结合二进制观察图像得到的朴素理解）

 

对照式子可以发现  C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8(1000)时，k=3;

C[8] = A[8-2^3+1]+A[8-2^3+2]+......+A[8]

即为上面列出的式子

 

为此我们引用的一个函数 lowbit( )

int lowbit(int x)
{
    return x&(-x);
}

其作用是取出x最低位的1,其实不难看出lowbit(x)便是上面的2^k,因为2^k后面一定有k个0

比如说2^5==>100000

正好是i最低位的1加上后缀0所得的值。

 

那么我们还是会很好奇这个二进制运算是如何实现这种计算的？

我们知道,对于一个数的负数就等于对这个数取反+1，以二进制数11010为例:11010的补码为00101,加1后为00110,两者相与便是最低位的1。其实很好理解,补码和原码必然相反,所以原码有0的部位补码全是1,补码再+1之后由于进位那么最末尾的1和原码。最右边的1一定是同一个位置(当遇到第一个1的时候补码此位为0,由于前面会进一位,所以此位会变为1)，所以我们只需要进行a&(-a)就可以取出最低位的1了。

会了lowbit,我们就可以进行区间查询和单点更新了

 

3.单点更新

继续看开始给出的图,此时如果我们要更改a[1]

则有以下需要进行同步更新

1(001)        C[1]+=a[1]

lowbit(1)=001 1+lowbit(1)=2(010)     C[2]+=a[1]

lowbit(2)=010 2+lowbit(2)=4(100)     C[4]+=a[1]

lowbit(4)=100 4+lowbit(4)=8(1000)   C[8]+=a[1]

转化成代码：

void update(int x,int d)
{
    while(x<=n)
    {
        c[x]+=d;
        x+=lowbit(x);
    }
}
//x为更新后的位置，d为更新的值，n为数组的最大值

 

4.区间查询

举个例子 i=5

C[4]=A[1]+A[2]+A[3]+A[4]; 

C[5]=A[5];

可以推出:   sum(i = 5)  ==> C[4]+C[5];

序号写为二进制: sum(101)=C[(100)]+C[(101)];

第一次101,减去最低位的1就是100;

其实也就是单点更新的逆操作

代码如下:

int Getsum(int x)
{
    int s=0;
    while(x>0)
    {
        s+=c[x];
        x-=lowbit(x);
    }
    return s;
}

sum(x)就是a[x]的前缀和，想查询l~r区间的元素和只需要求出来sum(r)-sum(l-1)。

 

模板代码：

 1 int lowbit(int x)
 2 {
 3     return x&(-x);
 4 }
 5 int Getsum(int x)
 6 {
 7     int s=0;
 8     while(x>0)
 9     {
10         s+=c[x];
11         x-=lowbit(x);
12     }
13     return s;
14 }
15 void update(int x,int d)
16 {
17     while(x<=n)
18     {
19         c[x]+=d;
20         x+=lowbit(x);
21     }
22 }