浅谈树状数组

Posted 2020-10-30 天下风云出我辈

　　树状数组是一种数据结构，支持一些区间操作，比线段树好写，同样也比线段树的功能少一些。

　　先来看一张图（摘自百度百科）

　　　　　　　　　　　　　　　　　　

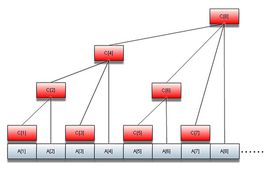
　　树状数组就是这个样子的，但是树状数组的空间复杂度是O(n)的，它不像线段树那样每个节点的信息都上传的父亲去保存，他是由某一位来保存前一段区间的信息，比如说和。那么是哪一位又是保存多长的区间那？这就到了数状数组的主角lowbit上场了，lowbit是一个很简单又很复杂的东西，说它简单是因为写起来非常的简单，说它复杂是因为理解起来比较麻烦，lowbit（x）的功能是求出来x的二进制中最后一个1是多少，举个例子lowbit（7）=1，因为7的二进制是111，它的最后一个1是1，而lowbit（6）=2，因为6的二进制是110，它的最后一个1是2.

　　有的讲树状数组的是把lowbit的原理讲了一遍的，个人感觉没用其实是窝不会，只需要记得lowbit(x)的求法是x&(-x)就好了，然后树状数组的第i位记录的就是从i-lowbit(i)+1开始到i这一段的信息，也就是从i往前lowbit（i）那么长，总之这样沿着lowbit就可以做到不重不漏了。

　　树状数组最基本的操作就是点修改区间查询，点修改区间查询和区间修改点查询。

1.点修改区间查询

　　点修改不只是要修改一个点，还要把记录了这个点的信息的那些点也修改了，这时还是要沿着lowbit走，当前点不断的加lowbit，每次到的点都修改一下，而区间查询就更容易了，如果查询区间是[l,r]，那么久查询一下[1,r]，在查询一下[1,l-1]然后相减久ok了，然后查询就是沿着lowbit减，把每一位的数加起来，好比查询[1,7],就查7，[5,6],[1,4]就可以了。

模板：https://www.luogu.org/problemnew/show/P3374

 1 #include<iostream>
 2 #include<cstdio>
 3 using namespace std;
 4 const int maxn=10002;
 5 int n,m;
 6 int tree[maxn];
 7 int x,y,opt;
 8 int lowbit(int x)
 9 {
10     return x&(-x);
11 }
12 void add(int x,int y)
13 {
14     for(int i=x;i<=10000;i+=lowbit(x))
15         tree[i]+=y;
16 }
17 int query(int x)
18 {
19     int ans=0;
20     for(int i=x;i>=1;i-=lowbit(i))
21         ans+=tree[i];
22     return ans;
23 }
24 int main()
25 {
26     scanf("%d%d",&n,&m);//n个数，m个操作
27     for(int i=1;i<=n;++i)
28     {
29         scanf("%d",&x);
30         add(i,x);
31     } 
32     while(m--)
33     {
34         scanf("%d",&opt);
35         if(opt==1)
36         {
37             scanf("%d%d",&x,&y);
38             add(x,y);
39         }
40         else 
41         {
42             scanf("%d%d",&x,&y);
43             printf("%d\\n",query(y)-query(x-1)); 
44         } 
45     }
46     return 0;
47 } 

View Code

2.区间修改点查询

 　　用一个差分的思想转变成点修改区间查询。也就是把每一个数和前面的数做一下差，然后把这个新的数组放入树状数组中，这样区间修改就是在l那里加一下 ，在r+1那里减一下，而点查询则变成了查询[1,x]。

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=500005; 
template<typename T>void read(T &a)
{
    int f=1,x=0;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch==\'-\')f=0;ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<3)+(x<<1)+ch-\'0\';ch=getchar();
    }
    a=f?x:-x;
}
int n,m;
int tree[maxn];
int a[maxn];
int opt,x,y,k;
int lowbit(int x)
{
    return x&(-x);
}
void add(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i))tree[i]+=y;
}
int ans;
int query(int x)
{
    int ans=0;
    for(int i=x;i;i-=lowbit(i))
        ans+=tree[i];
    return ans;
}
int main()
{
    read(n),read(m);
    for(int i=1;i<=n;++i)
        read(a[i]);
    for(int i=1;i<=n;++i)
        add(i,a[i]-a[i-1]);//要注意这里是后一个－前一个，而不是从第一个开始连环减，每一个数代表的都是当前数减前一位数，从1累加才是当前数值
//    for(int i=1;i<=n;++i)cout<<tree[i]<<endl;
//    cout<<"KKKKK"<<endl;
    while(m--)
    {
        read(opt);
        if(opt==1)
        {
            read(x),read(y),read(k);
            add(x,k),add(y+1,-k);
        }
        else{
            read(x);
            printf("%d\\n",query(x));
        }
    }
    return 0;
}

View Code

 

　　树状数组还有很多其他应用，比如cdq的时候用。还有二维树状数组，不过窝太弱了，不会这些qwq