数据结构AVL

Posted 2020-12-22 zhangbiao97

什么是AVL树？

首先，回忆一下二分搜索树的问题，在二分搜索树中有一个很严重的问题，什么问题呢？

在二分搜索树中如果顺序添加元素会转化为链表，这就会大大降低二分搜索树的效率。比如说1、2、3、4、5、6。

二分搜索树如图：

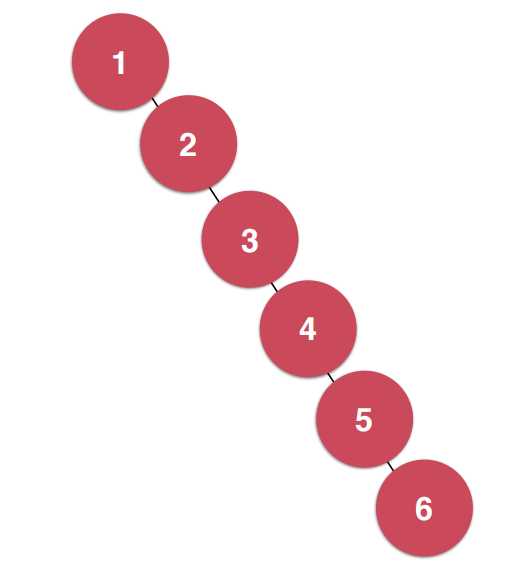
那么如何解决这个问题？

需要在二分搜索树的基础上添加一定的机制，使得二分搜索树能够维持平衡二叉树这样的性质。AVL树就是一种经典的平衡二叉树。

在AVL树中维护平衡型的条件是，对于任意一个节点，左子树和右子树的高度差不能超过1。

如图：

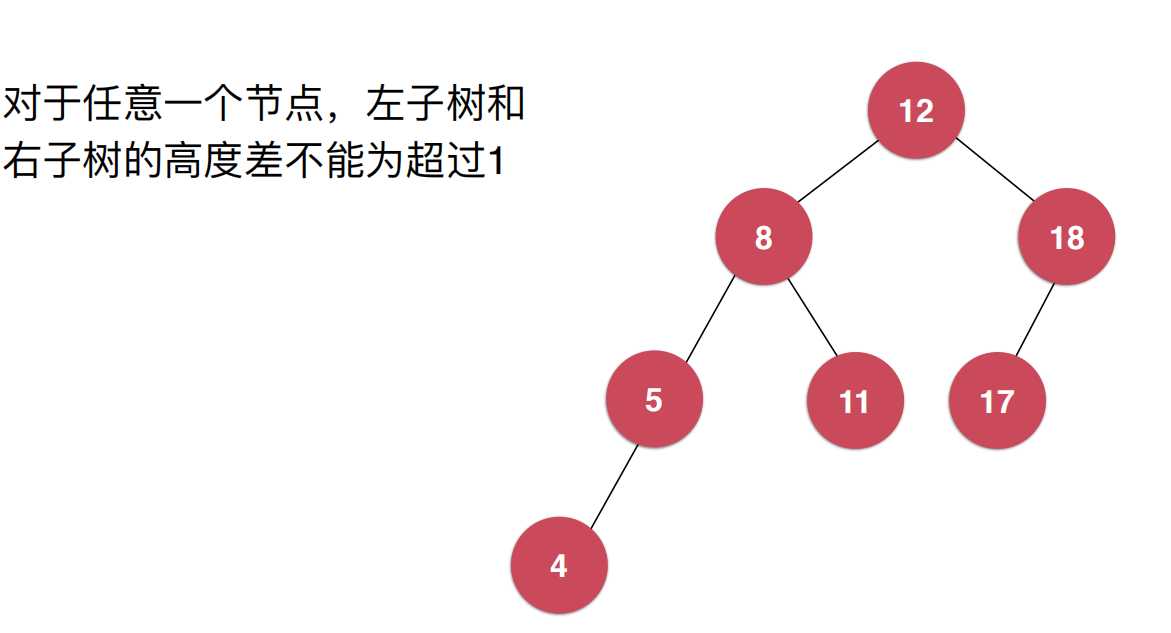
平衡因子：计算节点左右子树节点的高度差为该节点的平衡因子。平衡二叉树上所有节点的平衡因子只可能是-1、0、1。如果某个节点的平衡因子大于1则说明此树不是平衡二叉树。

如图：

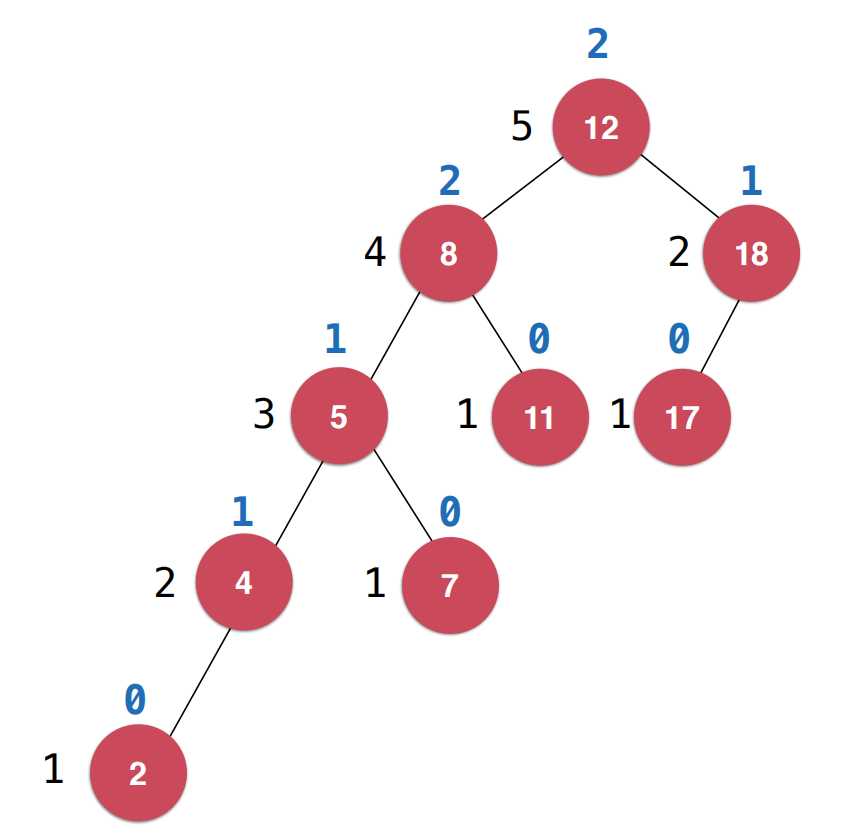
如果不是平衡二叉树，那么什么时候维护平衡呢？

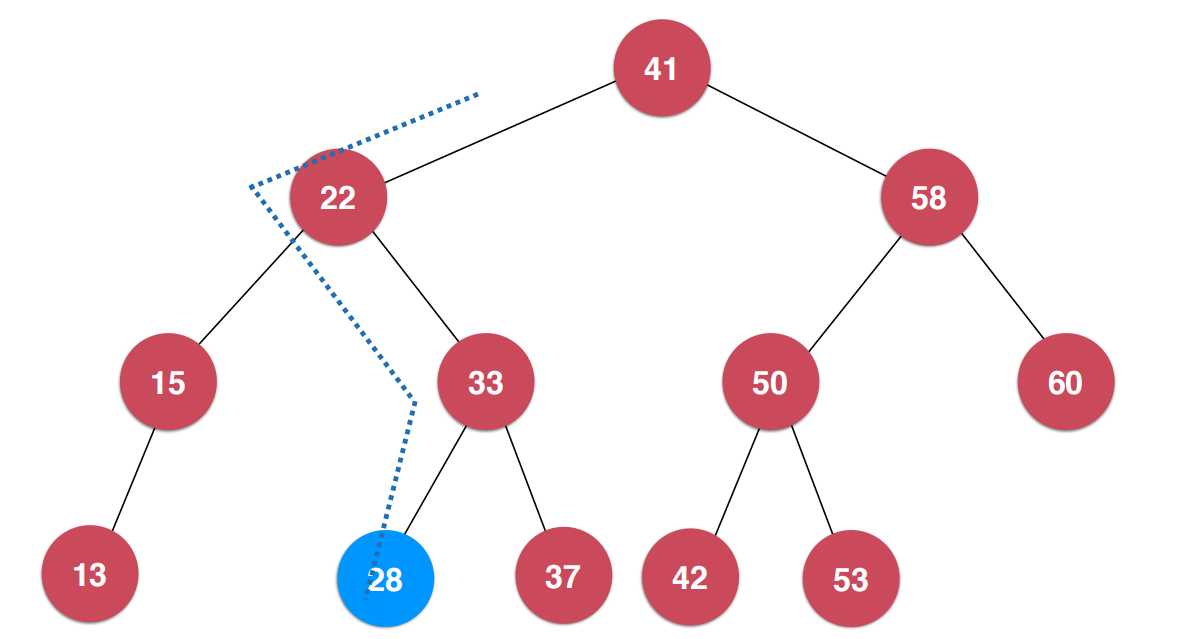
在二分搜索树中如果插入一个节点的话，会从根节点开始进行寻找，直到找到这个节点的正确位置，并且正确的位置一般都是叶子节点的位置。

大家可以想象一下，由于新添加了节点才有可能导致二分搜索树不再满足平衡性，那么相应的这个不平衡的节点只有可能发生在从我们插入的位置开始向父亲节点去找，发生在这些节点中，为什么呢？这是因为，在插入新节点后才破坏了整棵树的平衡性。

那么，破坏整棵树的平衡性，将反映在新节点的父亲节点或祖先节点，因为插入新节点之后它的父亲节点或祖先节点相应的左右子树的高度值需要进行更新，更新之后有可能平衡因子就会大于1或小于-1。

所以维护平衡的时机，应该是当我们添加节点之后，沿着该节点向上回溯来维护平衡性。

旋转操作

1、右旋转（LL）

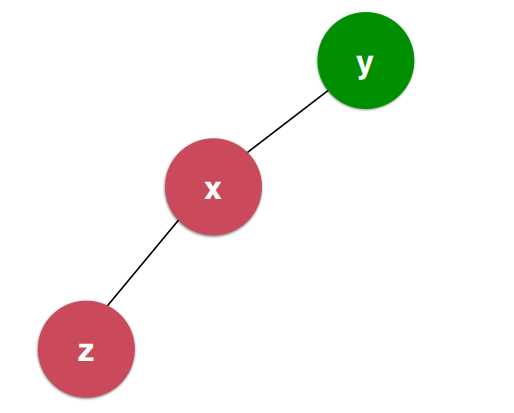
上图中，对于这个y节点来说，它已经不满足平衡二叉树的条件了，也就是说左子树的高度比右子树的告诉要高，并且这个高度差大于1，与此同时，它的左孩子也是这样的情况，左子树的高度大于等于右子树的。

以y节点为根节点的这颗子树整体不满足平衡二叉树的性质，并且整体是向左倾斜的，它们的右侧也有可能有子树。如图：

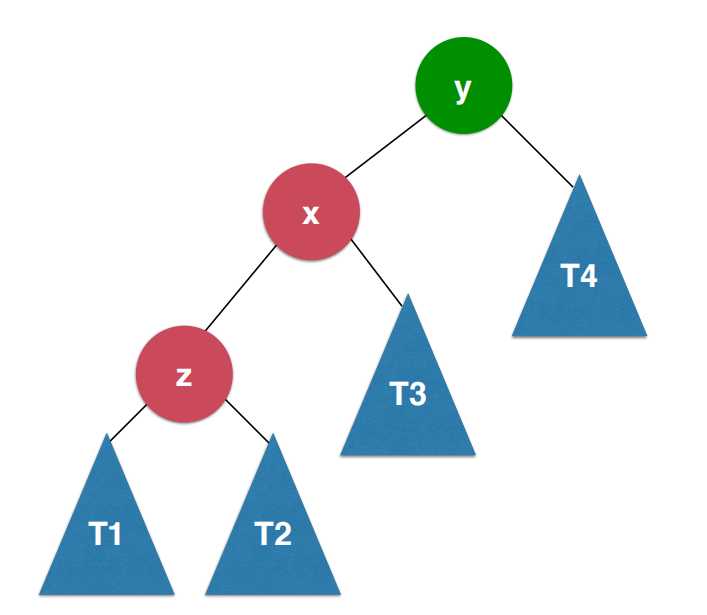
如上图，对于二分搜索树来说，它就会存在 T1 < z < T2 < x < T3 < y < T4 这样的关系。

在这个图中，y节点的左子树过于高了，所以经过一系列操作使得y节点保持平衡性，并且整颗子树不能够失去二分搜索树的性质，这个操作就叫作右旋转。

右旋转的过程：

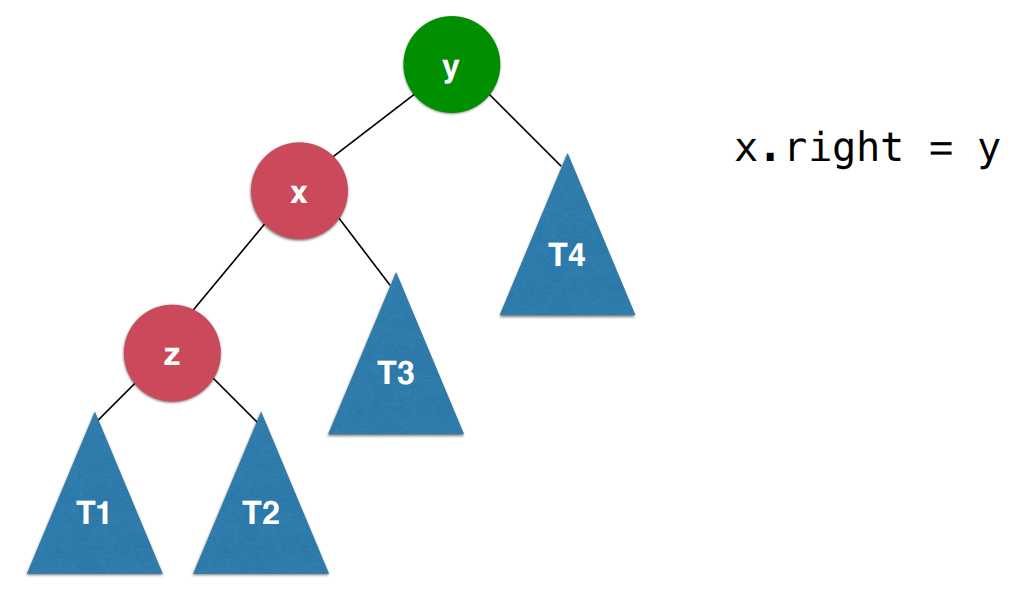
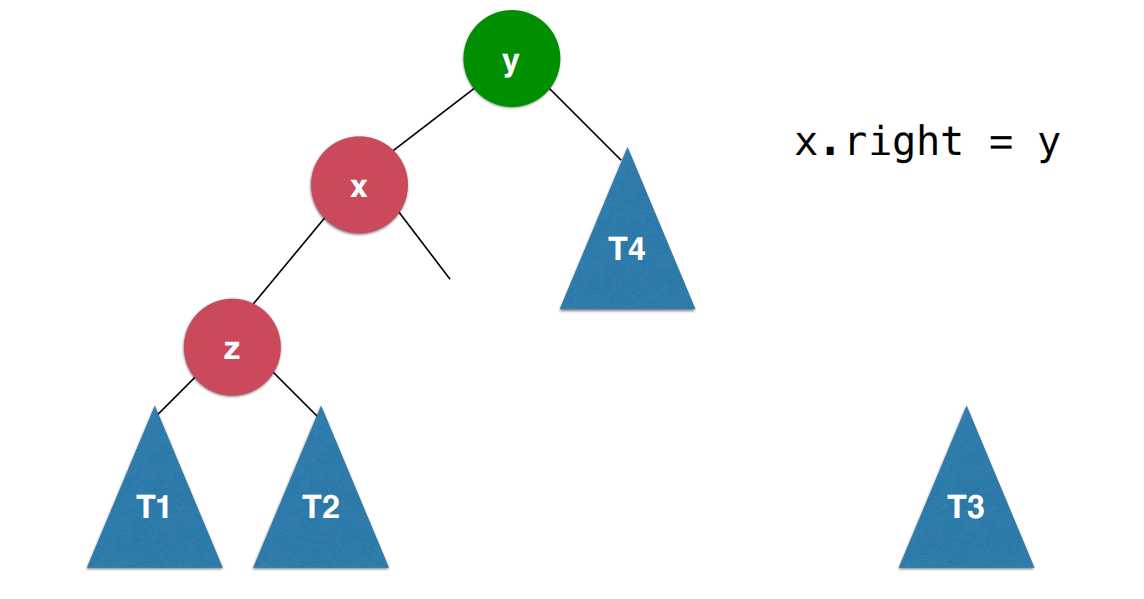
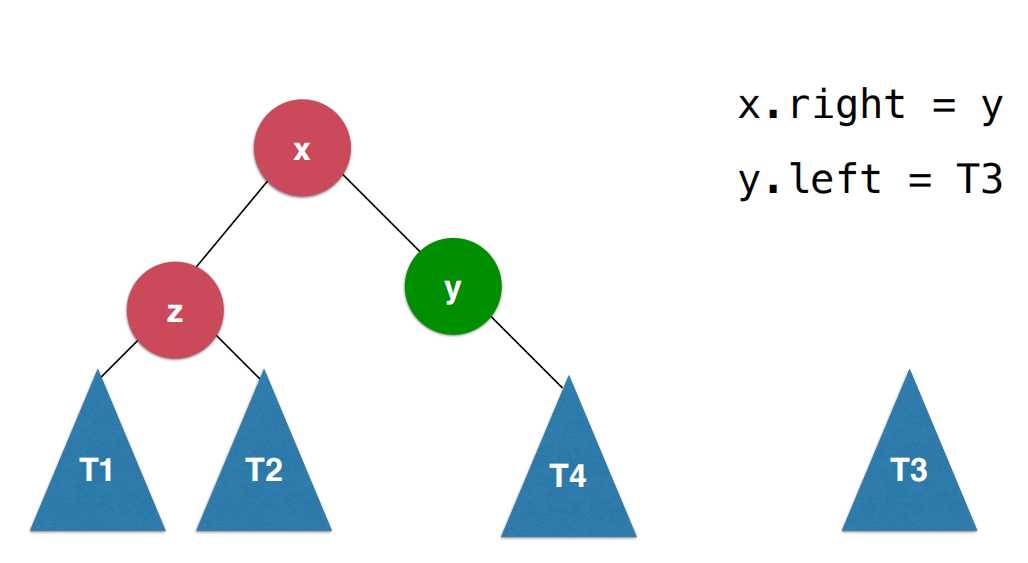
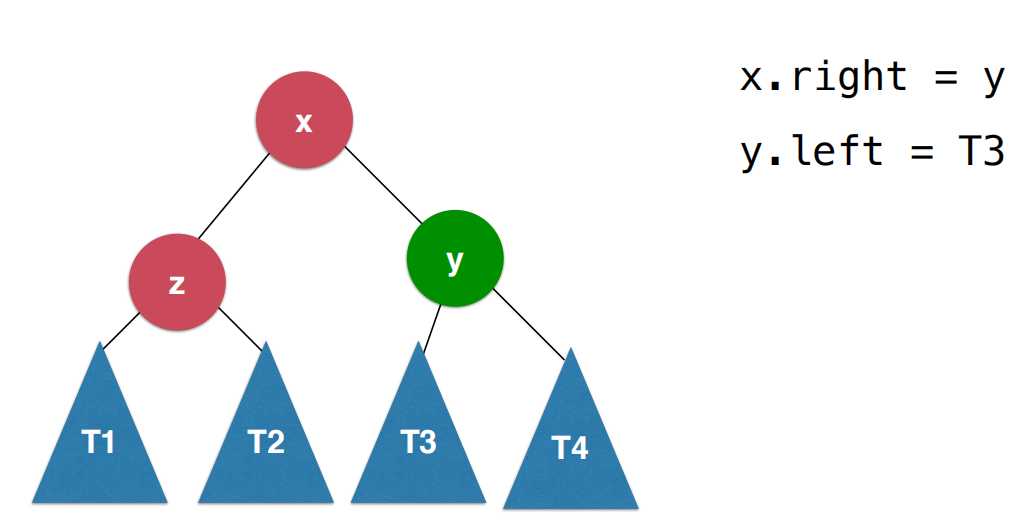
首先让x的右子树变成以y为根的子树，之后让y节点的左子树变成刚刚x节点的右子树T3，这样做完以后，让x变成新的二分搜索树的根节点，这样的过程就叫做右旋转。

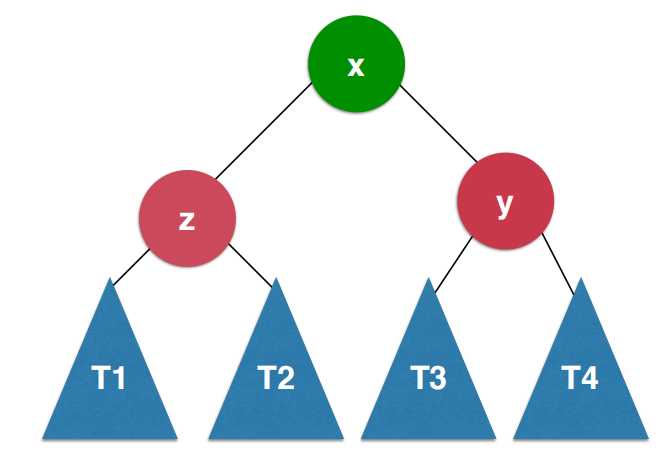
这个过程对于y节点来说，它顺时针转到x节点的右子树的位置，这个顺时针的方向从x的角度来看就是向右进行一个旋转，此时这颗树既满足二分搜索树的性质又满足平衡二叉树的性质。

如图：

2、左旋转（RR）

左旋转与右旋转相反，右旋转插入的元素在不平衡节点的左侧的左侧，而左旋转对应的要做的事情

就是要纠正如果插入的元素在不平衡节点的右侧的右侧。

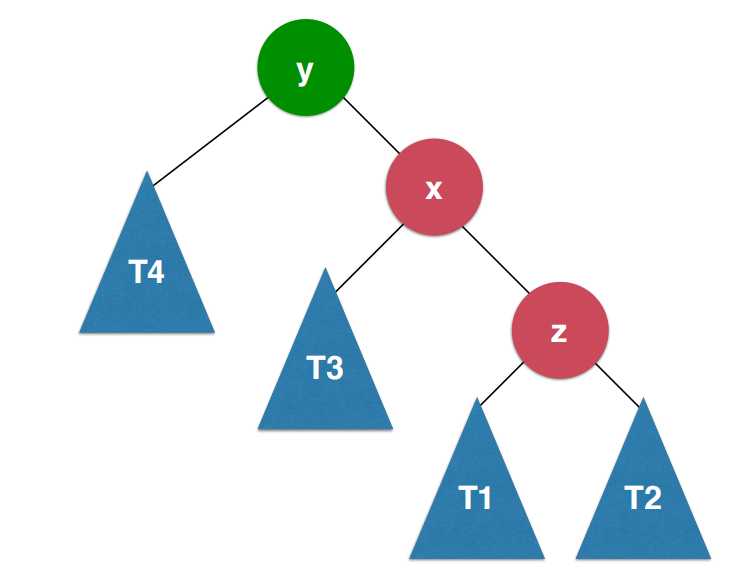
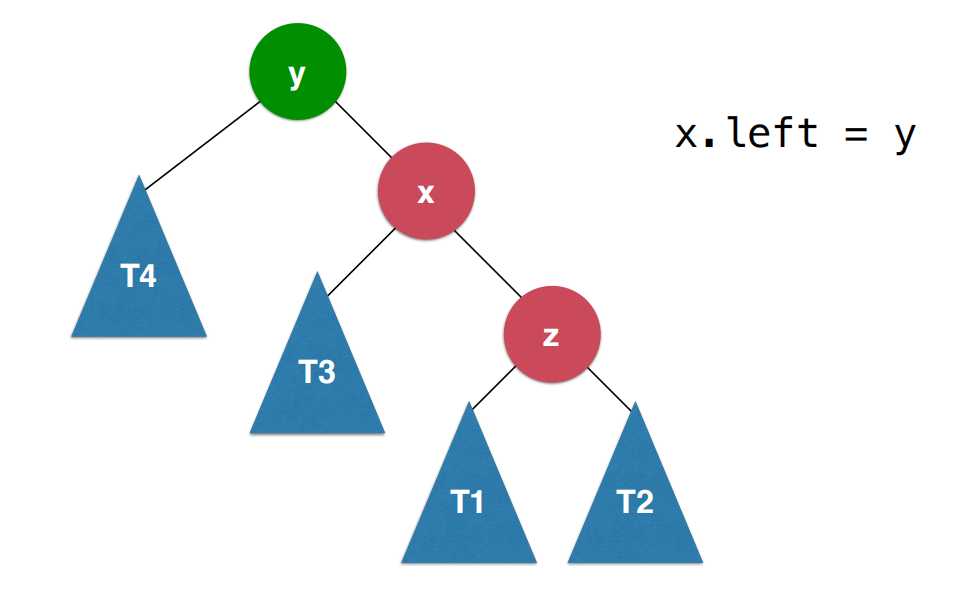
上图中，所展示的二叉树与右旋转所展示的二叉树完全是一个左右对称的情况，只不过对于这颗二叉树来说，当前不平衡节点为y的话，它的右子树高度值比左子树值相差大于1，换句话说左子树的高度值减去右子树的高度值小于-1，这样的情况下，要进行左旋转。

当前这颗二叉树的大小关系如下：T4 < y < T3 < x <T1 < z < T2

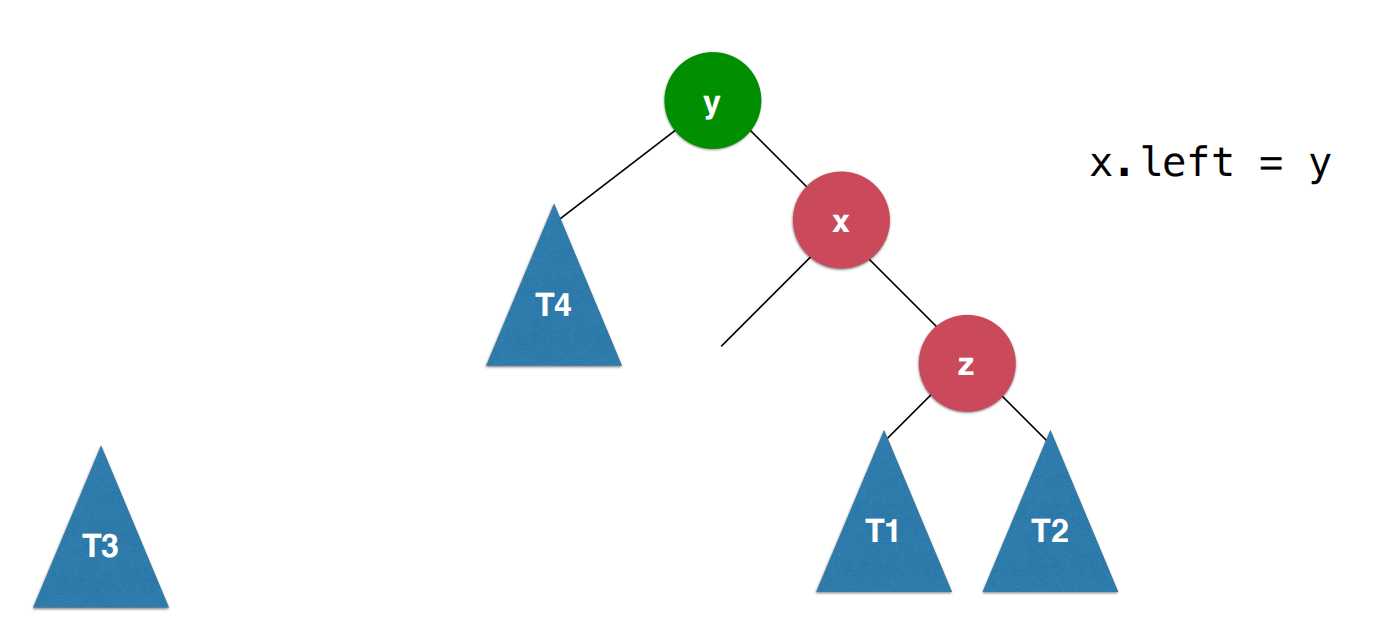
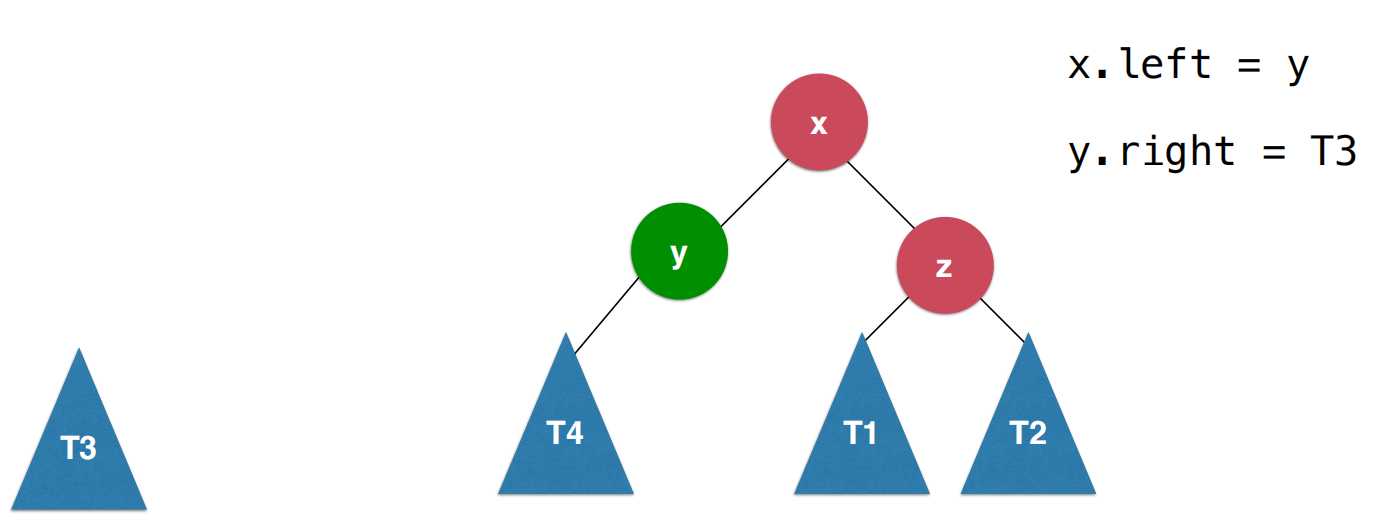
左旋转的过程：

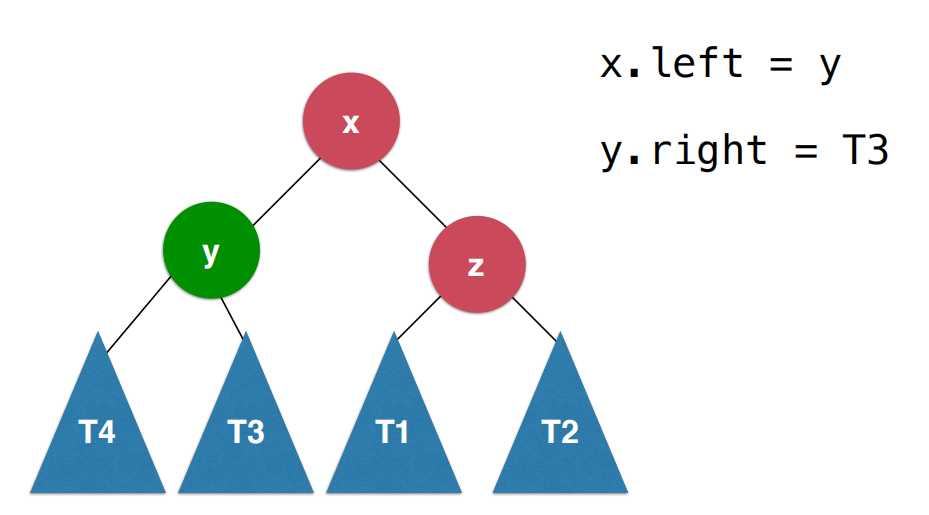
首先让x的左子树为y，之后让y的右子树为刚刚的x的左子树，这样以后让x变为新的根节点，这样的过程就叫做左旋转。

如图：

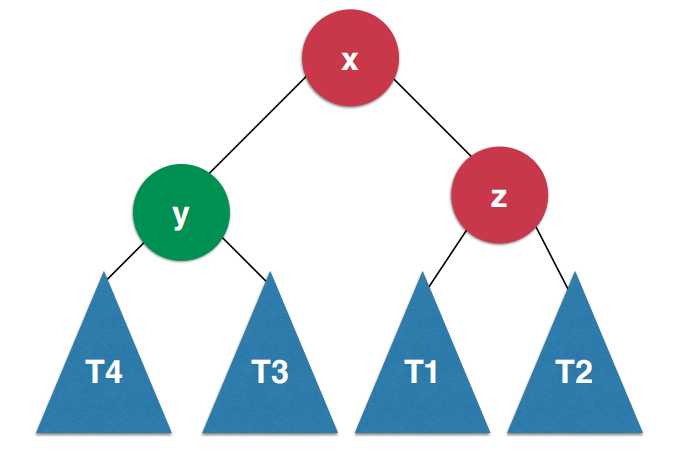
3、LR

LR的情况是插入的元素在左侧的右侧。如图：

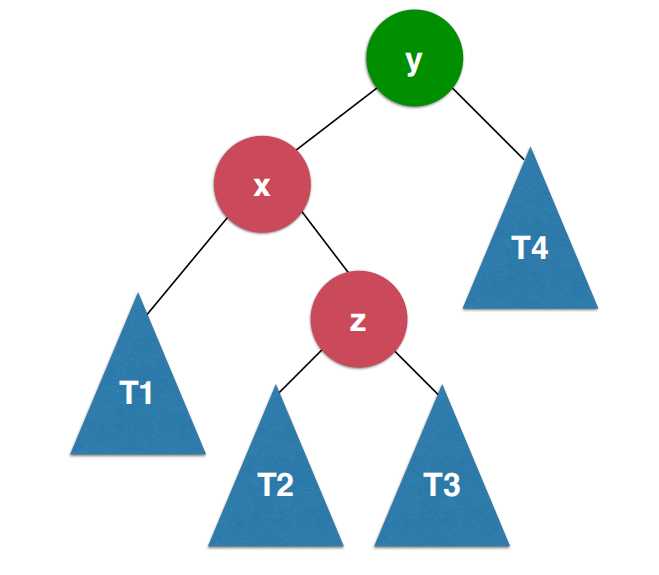
那么如何处理呢？

首先对x节点进行左旋转，转化为LL的情况。如图：

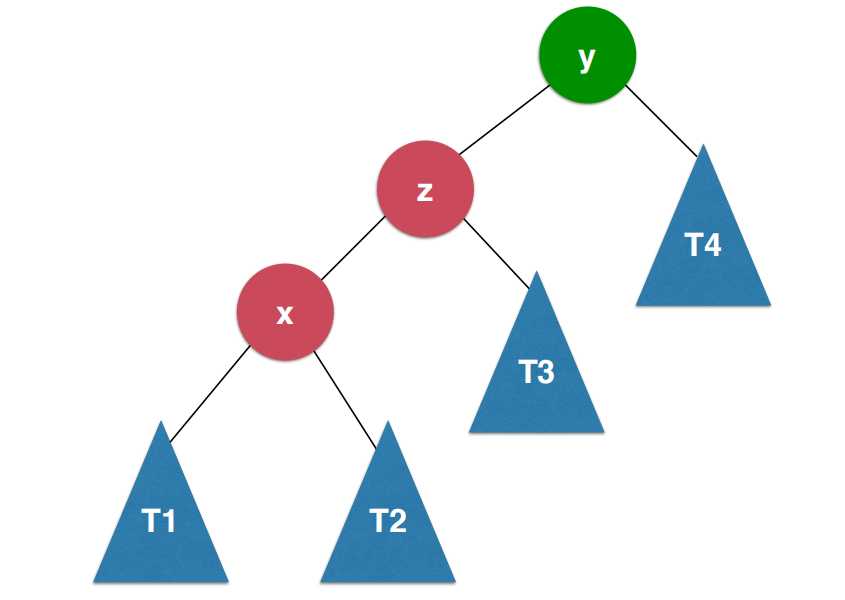
此时再对y节点进行右旋转。

4、RL

RL的情况是插入的元素在右侧的左侧。如图：

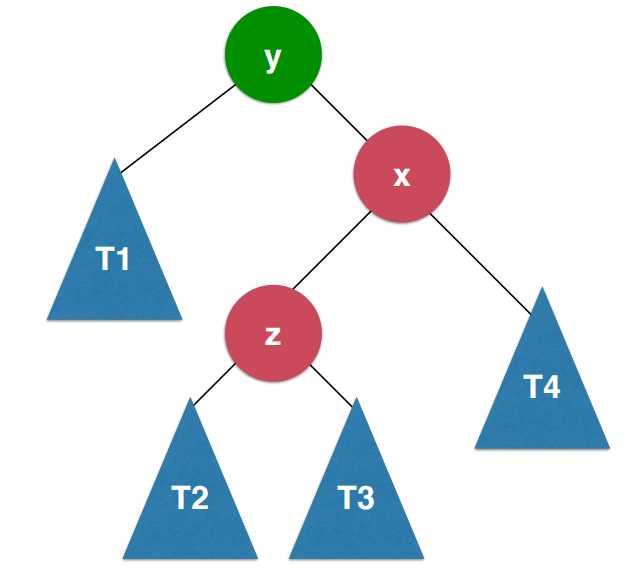
RL和LR处理的情况相反，首先对x节点进行右旋转，转化为RR的情况。如图：

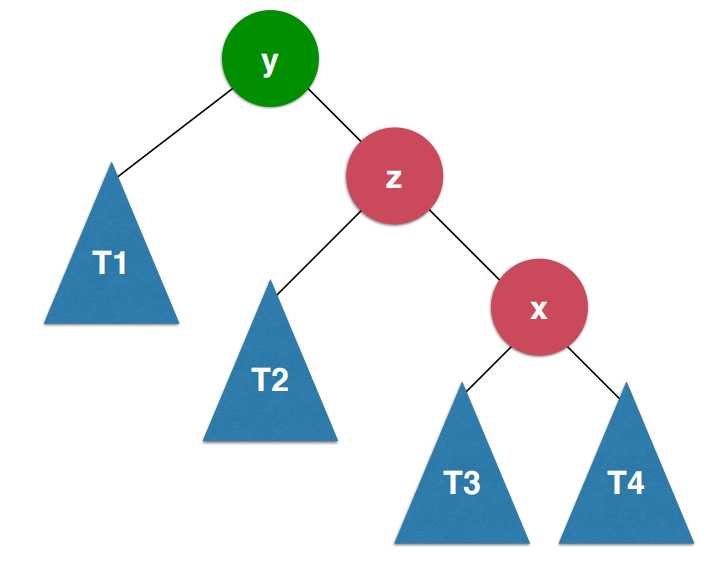
此时再对y节点进行左旋转。

AVL的实现

代码如下：

/**
 * 描述：平衡二叉树（AVL树）。
 * <p>
 * Create By ZhangBiao
 * 2020/5/17
 */
public class AVLTree<K extends Comparable<K>, V> {

    private Node root;

    private int size;

    public AVLTree() {
        this.root = null;
        this.size = 0;
    }

    @Override
    public void add(K key, V value) {
        root = add(root, key, value);
    }

    /**
     * 向以node为根节点的二分搜索树中插入元素(key, value)（递归算法）并返回插入新节点后二分搜索树的根节点
     *
     * @param node
     * @param key
     * @param value
     * @return
     */
    private Node add(Node node, K key, V value) {
        if (node == null) {
            size++;
            return new Node(key, value);
        }
        if (key.compareTo(node.key) < 0) {
            node.left = add(node.left, key, value);
        } else if (key.compareTo(node.key) > 0) {
            node.right = add(node.right, key, value);
        } else {
            node.value = value;
        }
        //更新height
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        //计算平衡因子
        int balanceFactor = getBalanceFactor(node);
        /*if (Math.abs(balanceFactor) > 1) {
            System.out.println("unbalanced: " + balanceFactor);
        }*/
        //平衡维护
        //LL
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }
        //RR
        if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
            return leftRotate(node);
        }
        //LR
        if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
        //RL
        if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

    /**
     * 返回以node为根节点的二分搜索树的最小值所在的节点
     *
     * @param node
     * @return
     */
    private Node minimum(Node node) {
        if (node.left == null) {
            return node;
        }
        return minimum(node.left);
    }

    /**
     * 删除掉以node为根的二分搜索树中的最小节点并返回删除节点后新的二分搜索树的根
     *
     * @param node
     * @return
     */
    private Node removeMin(Node node) {
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        node.left = removeMin(node.left);
        return node;
    }

    @Override
    public V remove(K key) {
        Node node = getNode(root, key);
        if (node != null) {
            root = remove(root, key);
            return node.value;
        }
        return null;
    }

    private Node remove(Node node, K key) {
        if (node == null) {
            return null;
        }
        Node retNode;
        if (key.compareTo(node.key) < 0) {
            node.left = remove(node.left, key);
            retNode = node;
        } else if (key.compareTo(node.key) > 0) {
            node.right = remove(node.right, key);
            retNode = node;
        } else {    //key.compareTo(node.key) == 0
            //待删除节点左子树为空的情况
            if (node.left == null) {
                Node rightNode = node.right;
                node.right = null;
                size--;
                retNode = rightNode;
            } else if (node.right == null) {
                //待删除节点右子树为空的情况
                Node leftNode = node.left;
                node.left = null;
                size--;
                retNode = leftNode;
            } else {
                Node successor = minimum(node.right);
                successor.right = remove(node.right, successor.key);
                successor.left = node.left;
                node.left = node.right = null;
                retNode = successor;
            }
        }
        if (retNode == null) {
            return null;
        }

        //更新height
        retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));

        //计算平衡因子
        int balanceFactor = getBalanceFactor(retNode);

        //平衡维护
        //LL
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
            return rightRotate(retNode);
        }
        //RR
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
            return leftRotate(retNode);
        }
        //LR
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
            retNode.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }
        //RL
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }
        return retNode;
    }

    @Override
    public boolean contains(K key) {
        return getNode(root, key) != null;
    }

    @Override
    public V get(K key) {
        Node node = getNode(root, key);
        return node == null ? null : node.value;
    }

    @Override
    public void set(K key, V newValue) {
        Node node = getNode(root, key);
        if (node == null) {
            throw new IllegalArgumentException(key + " not exist!");
        }
        node.value = newValue;
    }

    @Override
    public int getSize() {
        return this.size;
    }

    @Override
    public boolean isEmpty() {
        return this.size == 0;
    }

    /**
     * 获取节点node的高度
     *
     * @param node
     * @return
     */
    private int getHeight(Node node) {
        if (node == null) {
            return 0;
        }
        return node.height;
    }

    /**
     * 获取节点node的平衡因子
     *
     * @param node
     * @return
     */
    private int getBalanceFactor(Node node) {
        if (node == null) {
            return 0;
        }
        return getHeight(node.left) - getHeight(node.right);
    }

    /**
     * 判断该二叉树是否是一颗二分搜索树
     *
     * @return
     */
    public boolean isBST() {
        ArrayList<K> keys = new ArrayList<>();
        inOrder(root, keys);
        for (int i = 1; i < keys.size(); i++) {
            if (keys.get(i - 1).compareTo(keys.get(i)) > 0) {
                return false;
            }
        }
        return true;
    }

    private void inOrder(Node node, ArrayList<K> keys) {
        if (node == null) {
            return;
        }
        inOrder(node.left, keys);
        keys.add(node.key);
        inOrder(node.right, keys);
    }

    /**
     * 判断该二叉树是否是一颗平衡二叉树
     *
     * @return
     */
    public boolean isBalanced() {
        return isBalanced(root);
    }

    /**
     * 判断以node为根节点的二叉树是否是一颗平衡二叉树（递归算法）
     *
     * @param node
     * @return
     */
    private boolean isBalanced(Node node) {
        if (node == null) {
            return true;
        }
        int balanceFactor = getBalanceFactor(node);
        if (Math.abs(balanceFactor) > 1) {
            return false;
        }
        return isBalanced(node.left) && isBalanced(node.right);
    }

    // 对节点y进行向右旋转操作，返回旋转后新的根节点x
    //        y                              x
    //       /                            /       //      x   T4     向右旋转 (y)        z     y
    //     /        - - - - - - - ->    /    /     //    z   T3                       T1  T2 T3 T4
    //   /     // T1   T2
    private Node rightRotate(Node y) {
        Node x = y.left;
        Node T3 = x.right;
        //向右旋转过程
        x.right = y;
        y.left = T3;
        //更新height
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
        return x;
    }

    // 对节点y进行向左旋转操作，返回旋转后新的根节点x
    //    y                             x
    //  /                            /       // T1   x      向左旋转 (y)       y     z
    //     /    - - - - - - - ->   /    /     //   T2  z                     T1 T2 T3 T4
    //      /     //     T3 T4
    private Node leftRotate(Node y) {
        Node x = y.right;
        Node T2 = x.left;
        //向左旋转过程
        x.left = y;
        y.right = T2;
        //更新height
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
        return x;
    }

    /**
     * 返回以node为根节点的二分搜索树中key所在的节点
     *
     * @param node
     * @param key
     * @return
     */
    private Node getNode(Node node, K key) {
        if (node == null) {
            return null;
        }
        if (key.equals(node.key)) {
            return node;
        } else if (key.compareTo(node.key) < 0) {
            return getNode(node.left, key);
        } else {
            return getNode(node.right, key);
        }
    }

    private class Node {

        public K key;

        public V value;

        public Node left;

        public Node right;

        public int height;

        public Node(K key, V value, Node left, Node right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
            this.height = 1;
        }

        public Node(K key, V value) {
            this(key, value, null, null);
        }

        public Node() {
            this(null, null, null, null);
        }

    }

}