C++进阶数据结构_AVL树
Posted LHlucky_2
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C++进阶数据结构_AVL树相关的知识,希望对你有一定的参考价值。
文章目录
1.AVL树的基本概念
1.1为什么需要
set/map底层用的都是二叉搜索树,但是普通的二叉搜索树是有缺陷的,如果往树中插入的元素是有序的或者是接近有序的,那么树就越接近链表的形式,那么查找和插入的效率就变成了O(N)。
因此map、set等关联式容器的底层结构是对二叉搜索树进行了平衡处理的,即采用平衡二叉树搜索树(AVL树)
1.2性质
当向二叉搜索树中插入新的节点后,如果能保证每个节点的左右子树高度只差绝对值不超过1,即保证了这棵树是AVL树,即有如下量大特点:
左右子树都是AVL树
左右子树的高度之差(平衡因子)的绝对值不超过1
如果一棵二叉搜索树的高度是平衡的,它就是AVL树。它的查找效率为logn
1.3适用场景
AVL是一颗绝对平衡的二叉搜索树,要求每个节点的左右子树的高度差的绝对值不超过1,这样可以保证查询时候的时间复杂度为logN。
如果要对其进行结构上的修改操作,由于需要维护树的平衡,就会需要对树进行旋转,性能会非常低下
因此:如果需要一种查询高效且有序的数据结构(且数据的个数为静态)可以考虑AVL树,如果一个结构经常修改,就不太适合
2.AVL树的实现
2.1平衡因子的调节
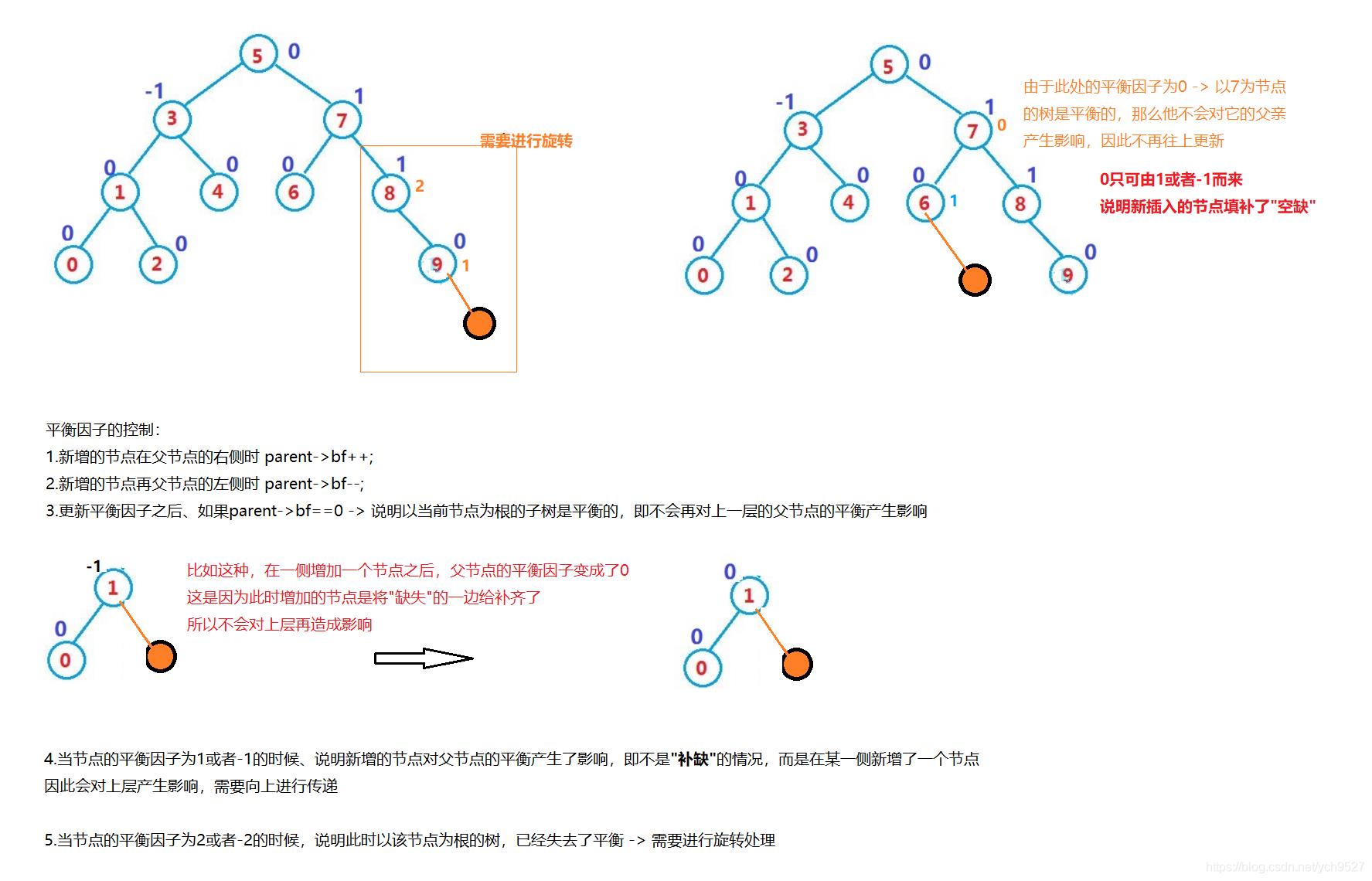
2.2几种旋转情况
2.2.1右单旋
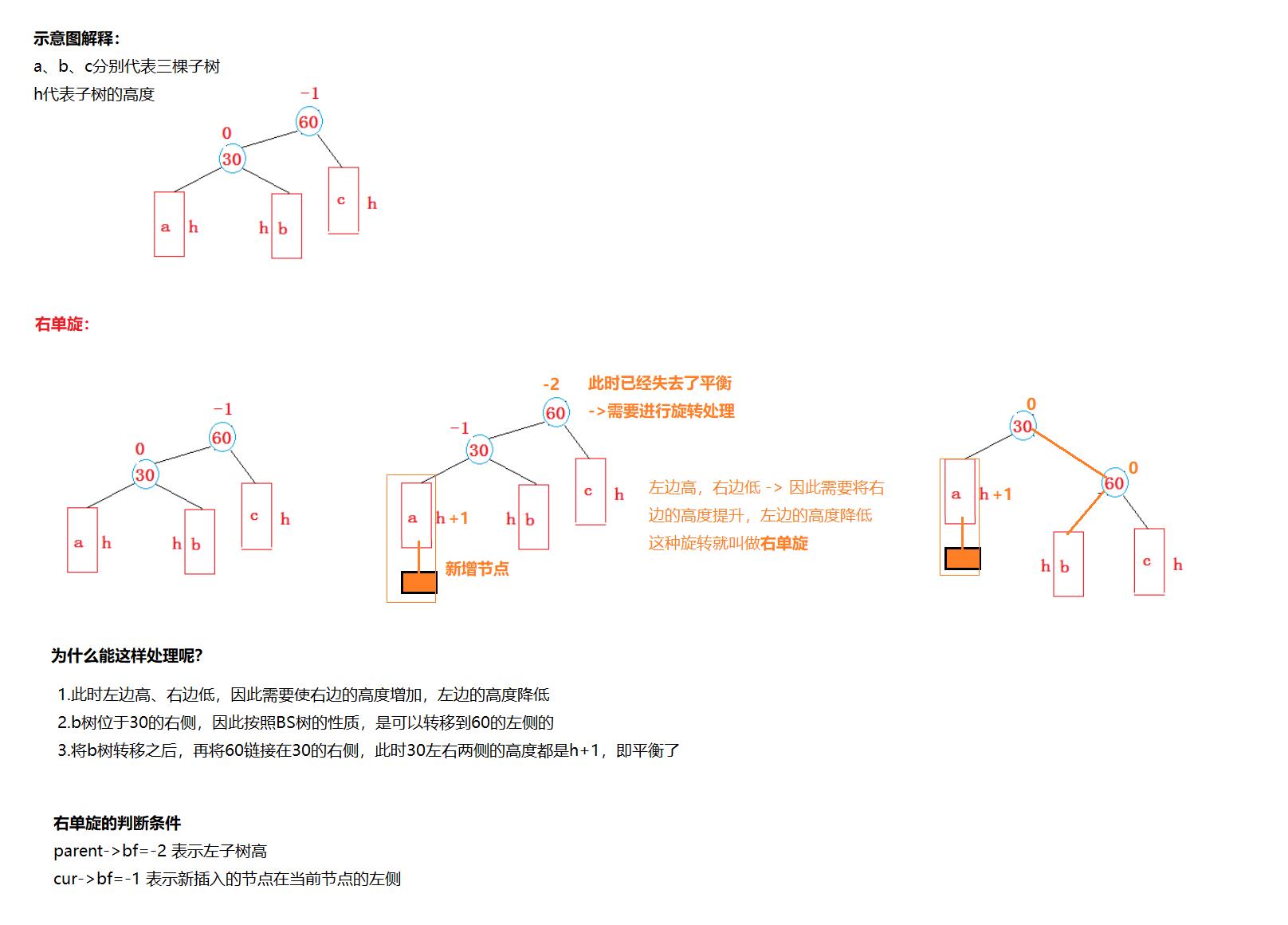
实现代码:
void RotateR(Node *parent)
{
Node *subL = parent->_left;//此时p->bf=-2,左边肯定不为空
Node *subR = subL->_right;
Node *pparent = parent->_parent;//保存一根
//将子树链接到parent的左侧
parent->_left = subR;
if (subR)
subR->_parent = parent;
//将parent连接到subL的右侧
subL->_right = parent;
parent->_parent = subL;
//将subL与ppretn链接起来
if (pparent == nullptr)//subL变成新的根
{
_root = subL;
subL->_left = nullptr;
}
else//不为根
{
subL->_parent = pparent;
if (parent == pparent->_left)//在上一级节点的左侧
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
}
//平衡因子的更新
parent->_bf = 0;
subL->_bf = 0;
}
2.2.2左单旋
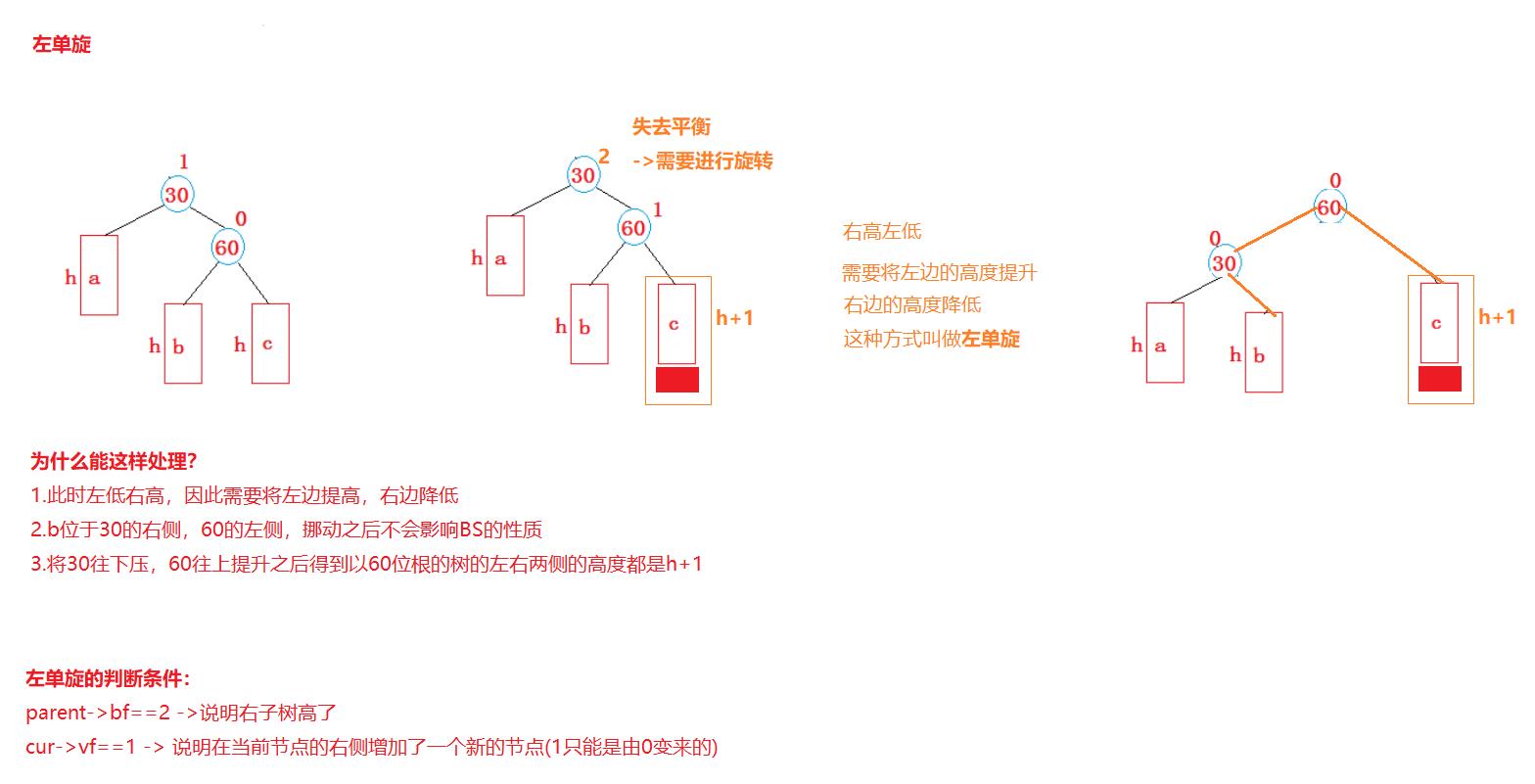
实现代码:
void RotateL(Node *parent)//左旋
{
Node *subR = parent->_right;//右变高,不可能为空
Node *subL = subR->_left;
Node *pprent = parent->_parent;
//subL连接到parent上
parent->_right = subL;
if (subL)
subL->_parent = parent;
//parent连接到subR上面
subR->_left = parent;
parent->_parent = subR;
//subR链接到pprent上
if (pprent == nullptr)//根
{
_root = subR;
subR->_parent = nullptr;
}
else//不为根
{
subR->_parent = pprent;
//判断链接在哪一侧
if (pprent->_left == parent)
{
pprent->_left = subR;
}
else
{
pprent->_right = subR;
}
}
//平衡因子的更新
parent->_bf = subR->_bf = 0;
}
2.2.3左右单旋
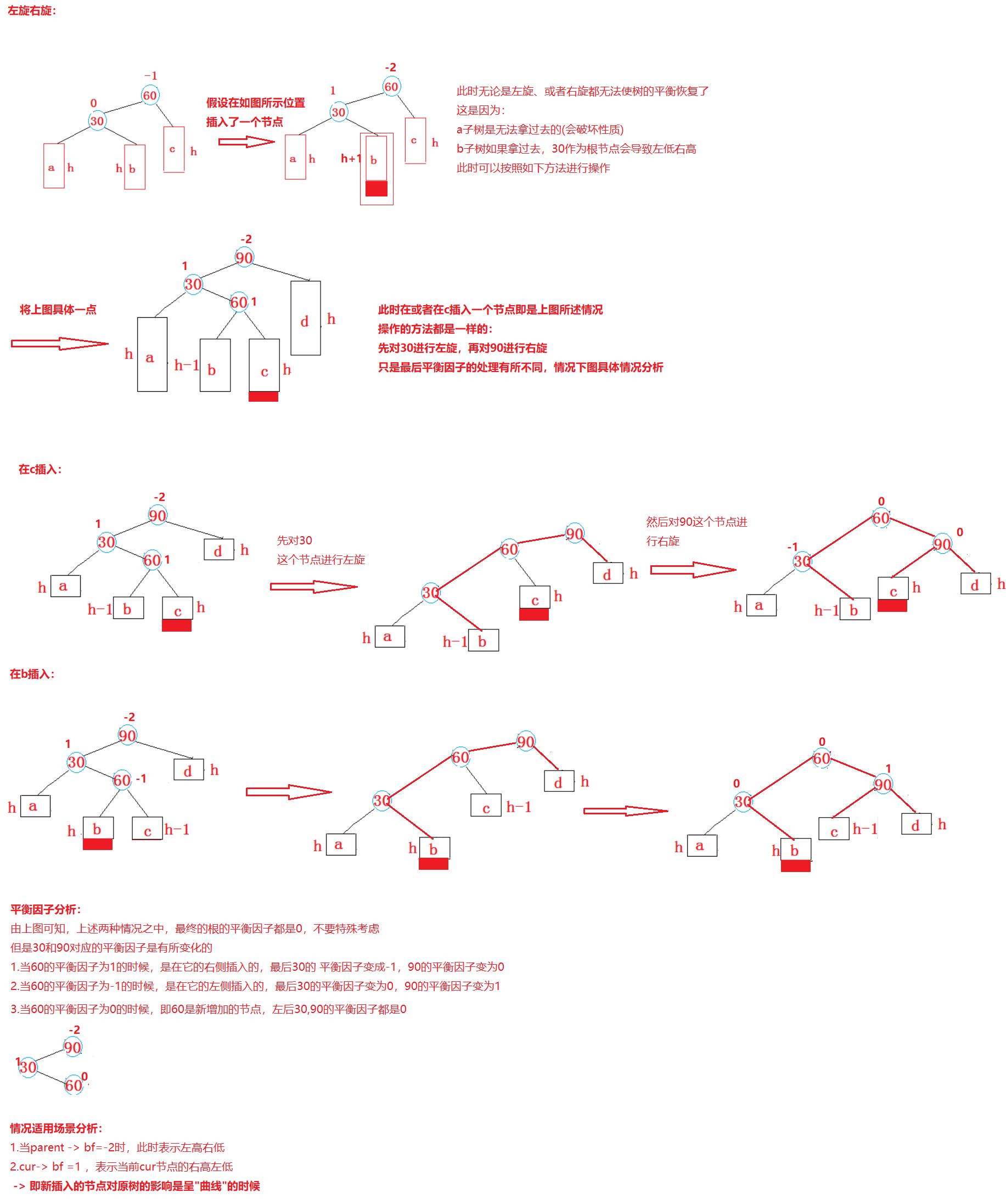
代码实现:
void RotateLR(Node *parent)
{
Node *subL = parent->_left;
Node *subLR = subL->_right;//此时不可能为空,因为右子树高
int bf = subLR->_bf;//保存一份平衡因子
RotateL(subL);//先左旋
RotateR(parent);//再右旋
//左旋、右旋会将平衡因子全部处理成0,因此要对平衡因子进行更改
if (bf == 1)//在subLR的右侧插入
{
subLR->_bf = 0;
subL->_bf = -1;
parent->_bf = 0;
}
else if(bf==-1)//在subLR左侧插入
{
subLR->_bf = 0;
subL->_bf = 1;
parent->_bf = 1;
}
}
2.2.4右左单旋
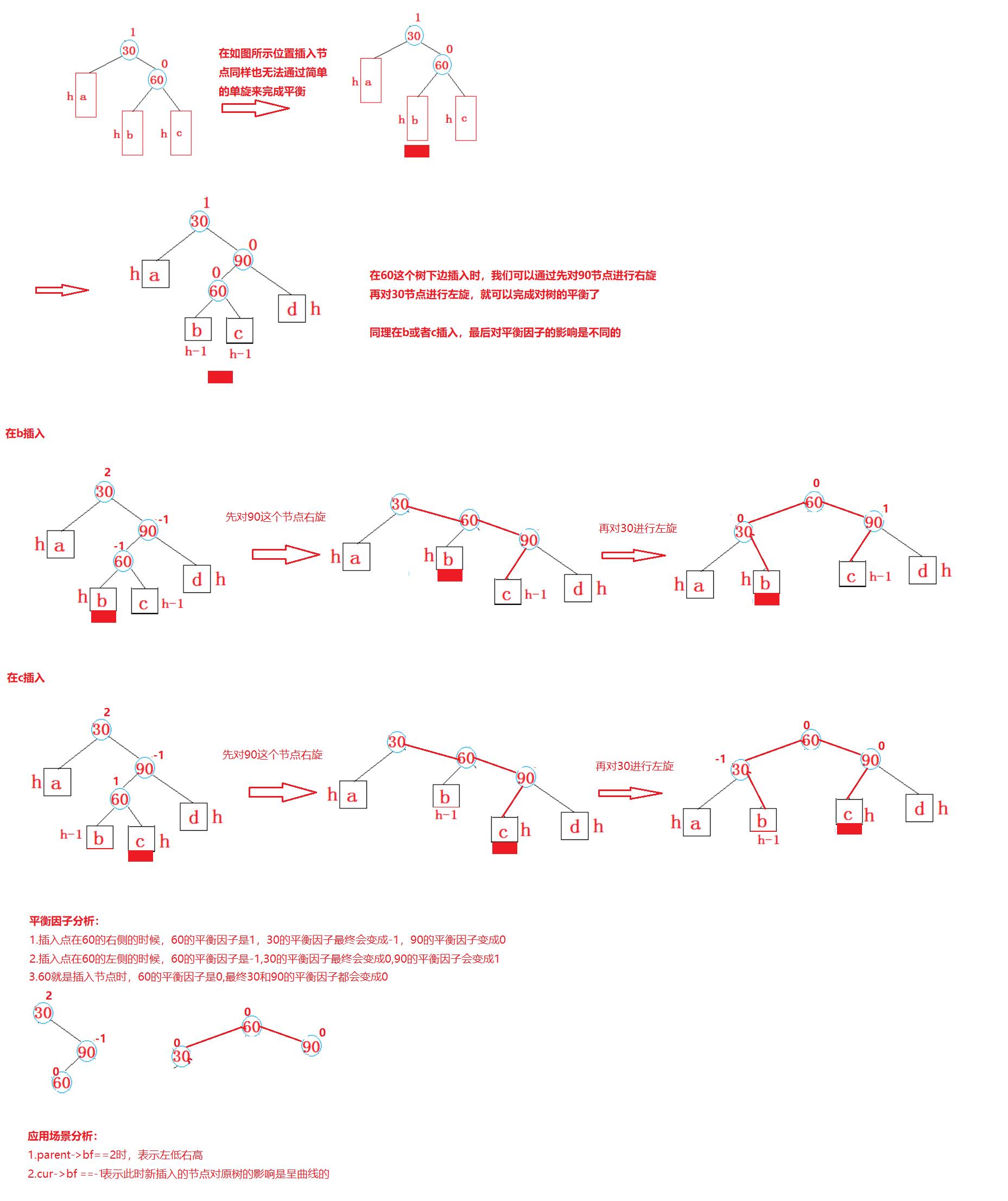
代码实现:
void RotateRL(Node *parent)
{
Node *subR = parent->_right;
Node *subRL = subR->_left;
int bf = subRL->_bf;
RotateR(subR);//先右旋
RotateL(parent);//再左旋
//平衡因子出来
if (bf == 1)//在subRL右侧插入时
{
subRL->_bf = 0;
parent->_bf = -1;
subR->_bf = 0;
}
else if(bf==-1)//在左侧插入时
{
subRL->_bf = 0;
parent->_bf = 0;
subR->_bf = 1;
}
}
3.整体代码即验证
3.1代码
#pragma once
using namespace std;
#include <iostream>
#include <map>
#include <string>
#include "assert.h"
#include <stdlib.h>
#include <vector>
template<class K,class V>
struct AVLTreeNode
{
AVLTreeNode(const pair<K, V>& kv=pair<K,V>())
:_left(nullptr)
,_right(nullptr)
, _parent(nullptr)
, _bf(0)
, _kv(kv)
{}
AVLTreeNode<K, V>*_left;
AVLTreeNode<K, V>*_right;
AVLTreeNode<K, V>*_parent;
pair<K, V> _kv;
int _bf;//平衡因子
};
template <class K,class V>
class AVLTree
{
public:
typedef struct AVLTreeNode<K,V> Node;
private:
//旋转函数编写
void RotateR(Node *parent)
{
Node *subL = parent->_left;//此时p->bf=-2,左边肯定不为空
Node *subLR = subL->_right;
Node *pparent = parent->_parent;//保存一份
//将子树链接到parent的左侧
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
//将parent连接到subL的右侧
subL->_right = parent;
parent->_parent = subL;
//将subL与ppretn链接起来
if (pparent == nullptr)//subL变成新的根
{
_root = subL;
subL->_parent = nullptr;
}
else//不为根
{
subL->_parent = pparent;
if (parent == pparent->_left)//在上一级节点的左侧
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
}
//平衡因子的更新
parent->_bf = 0;
subL->_bf = 0;
}
void RotateL(Node *parent)//左旋
{
Node *subR = parent->_right;//右变高,不可能为空
Node *subRL = subR->_left;
Node *pprent = parent->_parent;
//subL连接到parent上
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
//parent连接到subR上面
subR->_left = parent;
parent->_parent = subR;
//subR链接到pprent上
if (pprent == nullptr)//根
{
_root = subR;
subR->_parent = nullptr;
}
else//不为根
{
subR->_parent = pprent;
//判断链接在哪一侧
if (pprent->_left == parent)
{
pprent->_left = subR;
}
else
{
pprent->_right = subR;
}
}
//平衡因子的更新
parent->_bf = subR->_bf = 0;
}
void RotateLR(Node *parent)
{
Node *subL = parent->_left;
Node *subLR = subL->_right;//此时不可能为空,因为右子树高
int bf = subLR->_bf;//保存一份平衡因子
RotateL(subL);//先左旋
RotateR(parent);//再右旋
//左旋、右旋会将平衡因子全部处理成0,因此要对平衡因子进行更改
if (bf == 1)//在subLR的右侧插入
{
subLR->_bf = 0;
subL->_bf = -1;
parent->_bf = 0;
}
else if(bf==-1)//在subLR左侧插入
{
subLR->_bf = 0;
subL->_bf = 1;
parent->_bf = 1;
}
else//bf==0,新增的
{
subLR->_bf = subL->_bf = parent->_bf = 0;
}
}
void RotateRL(Node *parent)
{
Node *subR = parent->_right;
Node *subRL = subR->_left;
int bf = subRL->_bf;
RotateR(subR);//先右旋
RotateL(parent);//再左旋
//平衡因子出来
if (bf == 1)//在subRL右侧插入时
{
subRL->_bf = 0;
parent->_bf = -1;
subR->_bf = 0;
}
else if(bf==-1)//在左侧插入时
{
subRL->_bf = 0;
parent->_bf = 0;
subR->_bf = 1;
}
else//bf==0,新增的
{
subRL->_bf = parent->_bf = subR->_bf = 0;
}
}
public:
//插入函数
pair<Node*, bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return make_pair(_root,true);
}
//有根了,按照平衡二叉树的方法进行插入
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (kv.first<cur->_kv.first)//K值比较,小于往左边走
{
parent = cur;
cur = cur->_left;
}
else if (kv.first>cur->_kv.first)//往右走
{
parent = cur;
cur = cur->_right;
}
else//相等,返回已有元素的指针
{
return make_pair(cur, false);
}
}
//此时已经找到插入的位置了,判断插入在左边还是插入在右边
cur = new Node(kv);
if (parent->_kv.first > kv.first)//插在左边
{
parent->_left = cur;
cur->_parent = parent;//回指
}
else//插在右边
{
parent->_right = cur;
cur->_parent = parent;
}
//更新平衡因子
Node *newnode = cur;//cur会发生改变
while (parent)//不为空
{
if (parent->_left == cur)//cur在parent左侧
{
parent->_bf--;
}
else//右侧
{
parent->_bf++;
}
if (parent->_bf == 0)//当前树是平衡的
break;
else if (abs(parent->_bf) == 1)//继续往上面走
{
cur = parent;
parent = parent->_parent;
}
else if (abs(parent->_bf) == 2)//需要进行旋转处理
{
if (parent->_bf == -2)//左边高
{
if (cur->_bf == -1)//是在当前节点的左侧插入了节点 ->右单旋
{
RotateR(parent);
}
else//cur->_bf=1 ->曲线影响
{
RotateLR(parent);
}
}
else//右边高
{
if (cur->_bf == 1)//在当前节点的右侧插入了节点 -> 左单旋
{
RotateL(parent);
}
else//cur->_bf=-1 曲线影响
{
RotateRL(parent);
}
}
break;//旋转过后当前的树就是平衡的了,立即退出
}
else//0 1 2 -> 不可能走到这一步,走到这里说明发生了逻辑错误
{
assert(false);
}
}
return make_pair(newnode, true);//放到这里放回是因为需要更新平衡因子
}
private:
//遍历的时候 root为private外面无法拿到
//因此需要封装一层
void _Inorder(Node *root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_kv.first << " " << root->_kv.second << endl;
_Inorder(root->_right);
}
public:
//遍历
void Inorder()
{
_Inorder(_root);
}
Node* Find(const K &k)
{
Node *cur = _root;
while (cur)
{
if (cur->_kv.first > k)
cur = cur->_left;
else if (cur->_kv.first < k)
cur = cur->_right;
else
return cur;
}
return false;
}
V &operator [] (const K &k)//string、int、vector等等都可以是V,是由默认的构造函数的 int()=0
{
//插入函数返回的是pair<node*,bool>
return (((Insert(make_pair(k, V()))).first)->_kv).second;//返回的是引用,是可以修改的
}
//验证是否是平衡树
private:
int _Isbalance(Node* root)//采用后序遍历的方式验证
{
if (root == nullptr)
return 0;
int left = _Isbalance(root->_left);
int right = _Isbalance(root->_right);
cout << root->_bf << " "<<endl;
if (abs(root->_bf)>1||left==-1||right==-1||abs(left - right) > 1)//不满足条件返回-1
return -1;
return (int)fmax(left, right) + 1;//满足条件返回当前高度
}
public:
bool Isbalance()
{
if (_Isbalance(_root) == -1)
return false;
else
return true;
}
private :
Node *_root = nullptr;
};
3.2验证
#include "avl.hpp"
void test1(vector<int>&arr)
{
AVLTree<int,int> t1;
cout << "中序遍历输出节点----------------" << endl;
for (auto&e : arr)
{
t1[以上是关于C++进阶数据结构_AVL树的主要内容,如果未能解决你的问题,请参考以下文章