Matlab可视化小结

Posted 2020-12-16 shish

 

 

 

 

 

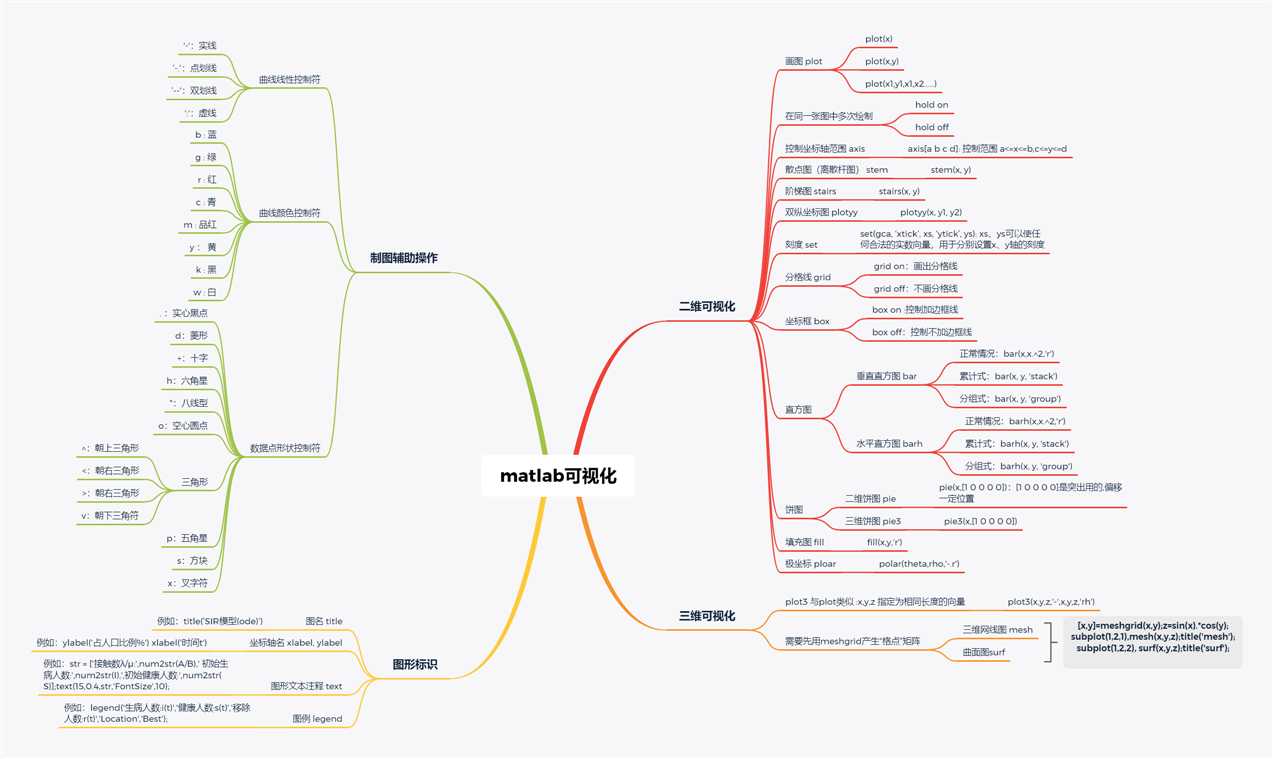
1. plot指令的基本调用格式

（1）plot(x)

x为向量时，以该元素的下标为横坐标、元素值为纵坐标绘出曲线

x为实数二维数组时，则按列绘制每列元素值相对其下标的曲线，曲线数等于x数组的列数。

x为复数二维数组时，则按列分别以数组的实部和虚部为横、纵坐标绘制多条曲线

（2）plot(x, y)

x、y为同维数组时，绘制以x、y元素为横纵坐标的曲线

x为向量，y为二维数组、且其列数或行数等于x的元素数时，绘制多条不同颜色的曲线

x为二维数组，y为向量时，情况与上相同，只是y仍为纵坐标。

（3）plot(x1, y1, x2, y2, …)

绘制以x1为横坐标、y1为纵坐标的曲线1，以x2为横坐标、y2为纵坐标的曲线2，等等。

其中x为横坐标，y为纵坐标，绘制y=f(x)函数曲线。

例子：

clc,clear,close;

x = 0:pi/100:2*pi;

y = 2*exp(-0.5*x).*sin(2*pi*x);

plot(y)

subplot(1,3,1); plot(y); title(‘plot(x)‘);

subplot(1,3,2); plot(x,y); title(‘plot(x,y)‘);

subplot(1,3,3); plot(x,y,[0:7],(2*[0:7] + 1)/100); title(‘plot(x1,y1,x2,y2)‘);

 

 

 

 

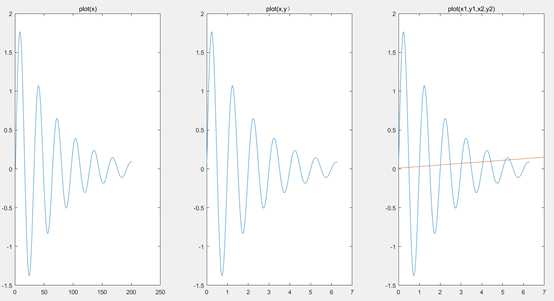
2. hold on hold off 在同一张图中多次绘制

例子

t = 0:pi/100:pi;

y1 = sin(t)‘ * [1, 0];

y2 = sin(t).*sin(3*t).*sin(-3*t).*sin(-t);

plot(t,y1,‘r-‘);

hold on

plot(t,y2,‘b‘);

hold off

 

 

 

 

 

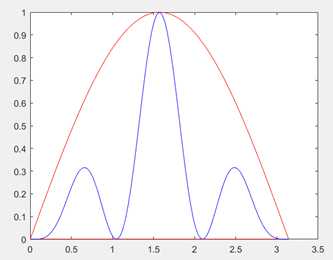
3. axis函数控制坐标轴

axis[a b c d] : 控制范围 a<=x<=b, c<=y<=d

例子

x = linspace(-15,15,200);

y = sin(4*x)./exp(.1*x);

plot(x,y,‘-r‘)

axis([-12 12 0 1.5])

 

4. stem画散点图

x = [0:pi/20:2*pi]‘;

y = [cos(x).*sin(x), sin(x)];

stem(x,y)

 

5. stairs画阶梯图

x = [0:pi/20:2*pi]‘;

y = [cos(x).*sin(x), sin(x)];

hold on

stem(x,y);

stairs(x,y,‘g‘);

hold off

 

 

 

6. plotyy指令画双纵坐标

x = 0:pi/100:2*pi;

y = 2*exp(-0.5*x).*sin(2*pi*x);

plotyy(x,y,[0:7],2*[0:7] + 1)

 

 

 

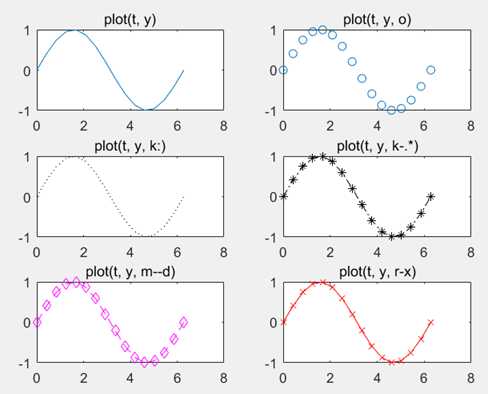
7. 制图辅助操作

 

 

 

 

 

 

 

 

 

 

t=(0:15)*2*pi/15;

y=sin(t);

subplot(3,2,1), plot(t, y); title(‘plot(t, y)‘)

subplot(3,2,2), plot(t, y, ‘o‘); title(‘plot(t, y, o)‘)

subplot(3,2,3), plot(t, y, ‘k:‘); title(‘plot(t, y, k:)‘)

subplot(3,2,4), plot(t, y, ‘k-.*‘); title(‘plot(t, y, k-.*)‘)

subplot(3,2,5), plot(t, y, ‘m--d‘); title(‘plot(t, y, m--d)‘)

subplot(3,2,6), plot(t, y, ‘r-x‘); title(‘plot(t, y, r-x)‘)

 

8. 刻度、分格线和坐标框

grid on         画出分格线

grid off         不画分格线

box on          控制加边框线

box off                 控制不加边框线

刻度设置

set(gca, ‘xtick’, xs, ‘ytick’, ys)

xs、ys可以使任何合法的实数向量，用于分别设置x、y轴的刻度。

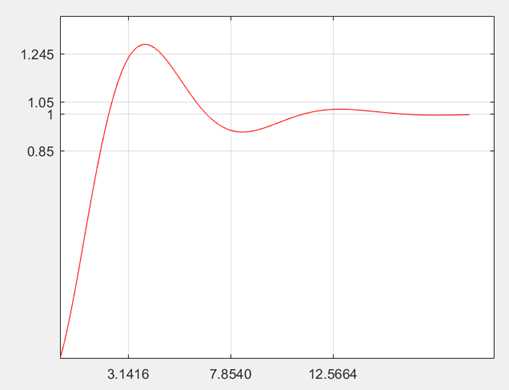
例题：

t = 6*pi*(0:100)/100;

y=1-exp(-0.3*t).*cos(0.7*t);                         

plot(t,y,‘r-‘);

grid on;

box on;

set(gca,‘xtick‘,[pi,2.5*pi,4*pi],‘ytick‘,[0.85,1,1.05,1.245]);

 

 

 

 

 

 

9. 图形标识

图名（title）

坐标轴名（xlabel、ylabel）

图形文本注释（text）

图例（legend）

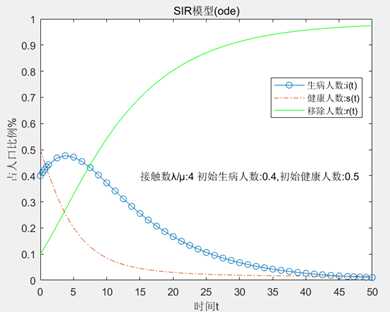
例（SIR,ode）：

A = 0.4;

B = 0.1;

I = 0.4;

S = 0.5;

tspan = [0 50];

y0 = [I S];

[t, y] = ode45(@(t,y)odefun(t,y,A,B), tspan, y0);

r = 1-y(:,1)-y(:,2);

plot(t,y(:,1),‘-o‘,t,y(:,2),‘-.‘,t,r,‘g‘);

hold on;

legend(‘生病人数:i(t)‘,‘健康人数:s(t)‘,‘移除人数:r(t)‘,‘Location‘,‘Best‘);

ylabel(‘占人口比例%‘);

xlabel(‘时间t‘);

str = [‘接触数λ/μ:‘,num2str(A/B),‘ 初始生病人数:‘,num2str(I),‘,初始健康人数:‘,num2str(S)];

text(15,0.4,str,‘FontSize‘,10);

title(‘SIR模型(ode)‘);

 

function dydt = odefun(t,y,A,B)

dydt = zeros(2,1);

dydt(1) = A*y(1)*y(2) - B*y(1);

dydt(2) = -A*y(1)*y(2);

end

 

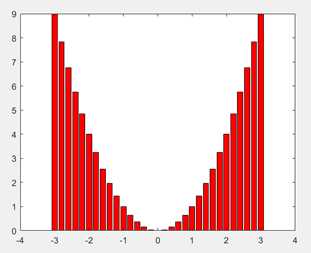
10. 直方图 bar

垂直直方图

x = -3:0.2:3;

bar(x,x.^2,‘r‘)

 

 

 

 

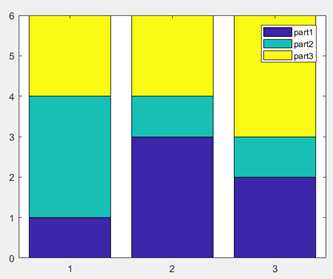
累计式

x=[1 2 3];

y=[1 3 2; 3 1 2; 2 1 3];

bar(x, y, ‘stack‘);

legend(‘part1‘, ‘part2‘, ‘part3‘);

 

 

 

 分组式

x=[1 2 3];

y=[1 3 2; 3 1 2; 2 1 3];

bar(x, y, ‘group‘);

legend(‘part1‘, ‘part2‘, ‘part3‘);

 

水平直方图 barh

累计式

分组式

x=[1 2 3];

y=[1 3 2; 3 1 2; 2 1 3];

barh(x, y, ‘group‘);

legend(‘part1‘, ‘part2‘, ‘part3‘);

 

 

 

 

11. 饼图pie

x=[1,2,3,4,5];

subplot(1,2,1);

pie(x,[1 0 0 0 0]);

legend({‘part1‘,‘part2‘,‘part3‘,‘part4‘,‘part5‘},‘Location‘,‘Best‘);

subplot(1,2,2);

y=int8(x==max(x))

pie3(x,y)

colormap(cool

 

 

 

12. 离散杆图stem

x = 0:0.1:2;

y = sin(x);

stem(x,y,‘r‘);

 

 

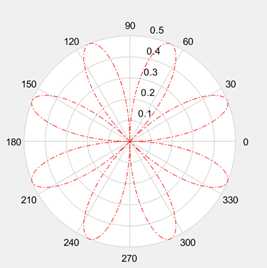
13.极坐标polar

theta = 0:0.01:2*pi;

rho = sin(2*theta).*cos(2*theta);

polar(theta,rho,‘-.r‘);

 

 

 

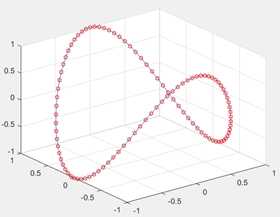
三维绘图

1. plot3 与plot类似 :x,y,z 指定为相同长度的向量

t=(0:0.02:2)*pi;

x=sin(t);

y=cos(t);

z=cos(2*t);

plot3(x,y,z,‘-‘,x,y,z,‘rh‘);

grid on;

 

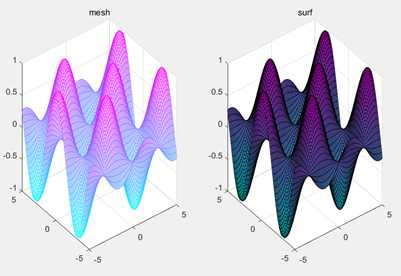
2. 三维网线图（mesh）

需要先用meshgrid产生“格点”矩阵

3. 曲面图（surf）

需要先用meshgrid产生“格点”矩阵

x=-5:0.1:5;

y=-5:0.1:5;

[x,y]=meshgrid(x,y);           

z=sin(x).*cos(y);                     

subplot(1,2,1), mesh(x,y,z);title(‘mesh‘);

subplot(1,2,2), surf(x,y,z);title(‘surf‘);   

colormap(cool);