莫比乌斯反演（HDU5663）

Posted 2020-12-14 jayshao

题意：

 

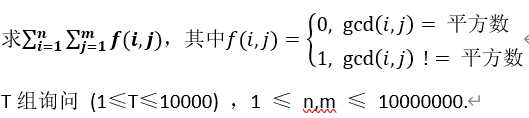
思路：

 

代码：

 1 const int maxn = 10000000 + 10;
 2 ll n, m, a;
 3 ll miu[maxn], v[maxn];
 4 ll sum[maxn];
 5 void Eratosthenes(int n) {
 6     for (int i = 1; i <= n; i++)miu[i] = 1, v[i] = 0;
 7     for (int i = 2; i <= n; ++i) {
 8         if (v[i])continue;
 9         miu[i] = -1;
10         for (int j = 2 * i; j <= n; j += i) {
11             v[j] = 1;
12             if ((j / i) % i == 0)miu[j] = 0;
13             else miu[j] *= -1;
14         }
15     }
16     for (int i = 1; i * i <= n; ++i) {
17         for (int j = i * i; j <= n; j += i * i) {
18             sum[j] += miu[j / (i * i)];
19         }
20     }
21     for (int i = 1; i <= n; ++i)sum[i] += sum[i - 1];
22 }
23 ll cal(int n, int m) {
24     ll ans = 0, pos;
25     for (int i = 1; i <= min(n, m); i = pos + 1) {
26         pos = min(n / (n / i), m / (m / i));
27         ans += 1ll * (sum[pos] - sum[i - 1]) * (n / i) * (m / i);
28     }
29     return ans;
30 }
31 
32 int main() {
33     Eratosthenes(10000000);
34     int T = read();
35     while (T--) {
36         n = read(), m = read();
37         printf("%lld
", n * m - cal(n, m));
38     }
39 }