HDU-1695(莫比乌斯反演)

Posted 2021-01-07 alingmaomao

题意：设a, b, c, d, k。 x属于[a, b], y属于[c, d]。问满足gcd(x, y)=k的（x, y）的对数是多少？注意：a=c=1；

公式推导：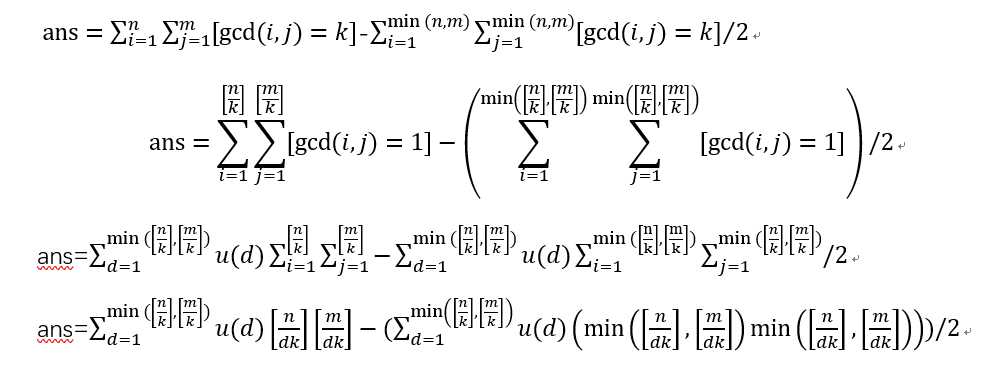

注意一下，中间过程别爆精度：

ac代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
const int N = 1e5 + 5;
bool vis[N];
int mu[N], prime[N];
void mobiws()
{
    int cnt = 0;
    mu[1] = 1;
    for (int i = 2; i < N; ++i)
    {
        if (!vis[i])
        {
            prime[++cnt] = i;    mu[i] = -1;
        }
        for (int j = 1; j<=cnt&&prime[j] * i < N; ++j)
        {
            vis[prime[j] * i] = 1;
            if (i%prime[j] == 0){ mu[prime[j] * i] = 0; break; }
            mu[prime[j] * i] =- mu[i];
        }
    }
    for (int i = 2; i < N; ++i)mu[i] += mu[i - 1];
}
ll cal(int n, int m, int d)
{
    if (!n || !m || !d)return 0;
    n /= d; m /= d;
    int last;
    ll ans = 0;
    for (int i = 1; i <= min(n, m); i = last + 1)
    {
        last = min(n / (n / i), m / (m / i));
        ans += (mu[last] - mu[i - 1])*(1LL)*(n / i)*(1LL)*(m / i);
    }
    return ans;
}
int main()
{
    mobiws();
    int t, a, b, c, d, k, cas = 0;
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
        printf("Case %d: ", ++cas);
        ll ans = cal(b, d, k) - cal(min(b, d), min(b, d), k)/2;
        printf("%lld
", ans);
    }
}