IEEE-754浮点计算精度问题

Posted 2020-12-14 lyc94620

前言

了解IEEE-754之前，先了解下什么是十进制和二进制，以及它们之间如何转化

十进制

十进制按照字面意思来理解，就是逢十进一，比如我们现在用的货币也好，计算也好，都是十进制，用0-9十个数字来表示

二进制

十进制十逢十进一，二进制就是二进一，用0和1来表示所有的数字

二进制转十进制

二进制转十进制，基本上是按位乘以2的n次方，再累加得到结果

比如二进制数1110.0101，转化为十进制

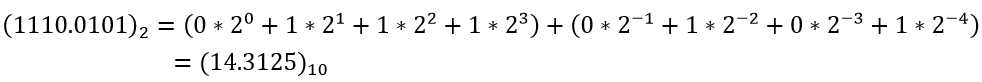
十进制转二进制

十进制转二进制，整数部分需要除以2，取余数，继续对结果除以2，直到余数为0；小数部分需要乘以2，取整数部分，继续对结果的小数部分乘以2，直到结果的小数部分为0

比如十进制数：13.125，转为二进制数的计算过程

整数部分是13，得到的二进制结果是

小数部分是0.125，得到的二进制结果是

 

什么是IEEE

IEEE二进制浮点数算术标准（IEEE 754）是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number）），一些特殊数值（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”；它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）。

IEEE 754规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80位实现）。只有32位模式有强制要求，其他都是选择性的。大部分编程语言都有提供IEEE浮点数格式与算术，但有些将其列为非必需的。例如，IEEE 754问世之前就有的C语言，有包括IEEE算术，但不算作强制要求（C语言的float通常是指IEEE单精确度，而double是指双精确度）。

 

IEEE浮点计算缺点

从上面的说明我们可以清楚的知道，IEEE就是基于二进制的浮点运算，我们日常使用的四则运算，也就是加减乘除，如果是使用IEEE标准进行处理的话，有可能会出现精度问题，比如十进制数0.1用二进制表示

 

从上面的计算结果可以看出，死循环了。。。也就是说十进制0.1是无法使用二进制准确表示的

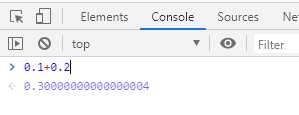
打开任何一个网站，F12进入开发者模式，在console中输入0.1+0.2，你会发现，结果的精度也有问题

 

既然会出现精度问题，但是为什么我们平时开发的过程中没有出现重大问题呢？

其实都是被忽悠的，由于我们平时的计算，四舍五入基本上就能得出我们想要的结果，编程语言在处理四则运算的时候其实会对一些无法准确表示的结果进行四舍五入等处理，造成一定的错觉

 

解决方案

大部分编程语言都使用浮点数进行运算，处理四则运算会造成精度问题，如果你需要高精度计算，那你必须使用其他方案

php：如果你的编程语言是PHP的话，而你又需要高精度运算，那你可以选择使用PHP的 bcMath 进行高精度运算

Java：如果你的编程语言是Java的话，高精度计算可以使用 BigDecimal 进行处理

 

总结

普通的四则运算，精度只是偶然的，误差时常发生，在处理金额等敏感问题时，尽量选择高精度的运算进行处理，避免出现不必要的麻烦

 

参考：IEEE-754