7-统计学-推断统计分析

Posted 2020-12-12 wgwg

推断统计

是研究如何利用样本数据来推断总体特征的统计方法

从样本信息外推到总体，以最终获得对总体问题的解答

今日内容

• 统计学的几个概念
• 概率分布
• 抽样分布
• 参数估计
• 假设检验

统计学的几个概念

变量

1 分类变量

• 无序分类变量

说明事物类别的一个名称，如性别有男女两种，二者无大小之分，无顺序之分，还有如血型、民族等

注：无大小之分，无顺序之分，仅知道属于哪个类别

• 有序分类变量

也是说明事物类型的一个名称，但是有次序之分，例如：满意度分为满意 一般 不满意，三者是有顺序的，但是无大小之分

注：无大小之分，但是有顺序之分，各个类别客户划分等级

2 数值型变量

• 连续型变量

取值范围是一个区间，它可以在该区间中连续取值，即连续型变量可以取到区间中的任意值，并且有度量单位。例如：身高、年龄、体重、金额

注：有大小之分，一定区间范围内取值个数无法确定

• 离散型变量

取值范围是有限个值或者一个数列构成的，表示分类情况，如：企业数量 产品数量等

注：有小大之分，一定区间范围内取值个数是有限的，可数的。

2 概率

随机事件：随机现象某种可能的观察结果称为随机事件

概率：刻画随机事件发生可能性大小，取值介于0-1之间，是经过大量的重复的独立的实验而得出的结论。

• 小概率事件

在统计学中，如果随机事件发生的概率小于或等于0.05，则认为是一个小概率事件，表示该事件在大多数情况下不会发生，并且一般认为小概率事件在一次随机抽样中不会发生，这就是小概率原理。小概率原理是推断统计的基础。

经典案例：? 瞎猫碰上死耗子

3 随机变量

随机事件的数量化

比如：还是抛硬币，出现正面，我们定义为“成功”，记为1，出现反面定义为“失败”，记为0,，那{0，1}就是本次实验的结果的量化值，为随机变量

离散型随机变量：随机变量X可以一一列举出来，在一定区间范围内X是有限个，可数的

例如抛硬币，X可取1或0

连续型随机变量：随机变量X无法一一列举，在一定区间范围内是无限个,

例如：统计北京市30岁以上男性身高，每个人的身高都不一样，测量单位一定的情况下，数据是连续的

4 总体和样本

总体：根据研究目的确定的所有个体某指标观察值（测量值）的集合

样本：在一个较大范围的研究对象中随机抽出一部分个体进行观察或预测，这些个体的测量值构成的集合称为样本。

大多数统计研究只能接触到样本，例如：灯泡检验是否合格只能通过样本

5 随机抽样

在抽样研究中，随机抽取一部分个体进行观察和测量的过程称为随机抽样

随机抽样的本质：每个个体最终是否入选在抽样进行前是不可知的，但是其入选的可能性是确切可知的（每个个体被抽到的概率是相等的）

注：随机≠随便

6 总体参数和统计量

总体参数：刻画总体特征的指标称为总体参数，例如：总体均值（μ），总体标准差（σ），总体比例 （π）

统计量：刻画样本特征的指标称为统计量，例如：样本均值（x-bar），样本标准差（s），样本比例（p）

但是往往总体参数都是不可知的，我们经常会通过样本统计量去估算总体参数。

7 抽样误差

许多总体指标是未知的，需要用相应的样本统计量对其进行估计。由随机抽样造成的样本统计量与总体指标之间的差异称为抽样误差（sampling error）

虽然在一次抽样研究中的抽样误差大小是随机的，但是抽样误差在概率意义下有规律可循，这种规律称为抽样分布，后面会详细讲到。

概率分布

随机变量的概率存在一定的规律，这个规律叫做概率分布，但是离散型随机变量和连续型随机变量的规律并不相同

离散型随机变量的概率分布有：二项分布、泊松分布；

连续型随机变量的概率分布：正态分布。

1 离散型随机变量的概率分布

二项分布

说到二项分布，不得不提一下他的前辈：伯努利分布

伯努利实验

在现实生活中，许多事件的结果往往只有两个。例如：抛硬币，正面朝上的结果只有两个：国徽或面值；检查某个产品的质量，其结果只有两个：合格或不合格；购买彩票，开奖后，这张彩票的结果只有两个：中奖或没中奖；拨打女朋友电话：接通或没接通。。。以上这些事件都可被称为伯努利试验

伯努利试验是单次随机试验，只有"成功（值为1）"或"失败（值为0）"这两种结果，是由瑞士科学家雅各布·伯努利(1654 - 1705)提出来的。

其概率分布称为伯努利分布(Bernoulli distribution)，也称为两点分布或者0-1分布，是最简单的离散型概率分布。我们记成功概率为p(0≤p≤1)，则失败概率为q=1-p，则概率：

 

 

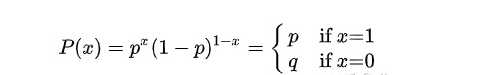
而二项分布是指在只有两个结果的n次独立的伯努利试验中，所期望的结果出现次数的概率

在单次试验中，结果A出现的概率为p，结果B出现的概率为q，p+q=1。那么在n=10，即10次试验中，结果A出现0次、1次、……、10次的概率各是多少呢？这样的概率分布呈现出什么特征呢？这就是二项分布所研究的内容

假设某个试验是伯努利试验，其成功概率用p表示，那么失败的概率为q=1-p。进行n次这样的试验，成功了x次，则失败次数为n-x，发生这种情况的概率可用下面公式来计算：

二项分布公式

 

 

 

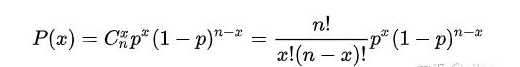
其中

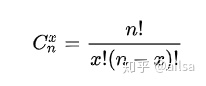
是二项式的计算方式 ！表示阶乘

上述案例使用Excel计算方式：

=BINOM.DIST(2,5,0.5,FALSE)

函数介绍

BINOM.DIST(number_s,trials,probability_s,cumulative)

BINOM.DIST 函数语法具有以下参数：

• Number_s 必需。 试验的成功次数。
• Trials 必需。 独立试验次数。
• Probability_s 必需。 每次试验成功的概率。
• cumulative 必需。 决定函数形式的逻辑值。 如果 cumulative 为 TRUE，则 BINOM.DIST 返回累积分布函数，即最多存在 number_s 次成功的概率；如果为 FALSE，则返回概率密度函数，即存在 number_s 次成功的概率。

二项分布的特征：

1.进行n次相同条件下的相互独立的重复试验

2.每次试验，只有2个结果，成功或者失败

3.出现成功的概率P每次试验是相同的，失败的概率q也是，并且p+q=1

如果符合上面的条件，那就是二项分布，如果上述试验只进行一次，就叫做伯努利试验，也是就二项分布是n次伯努利试验的结果。