《算法竞赛进阶指南》0x32约数

Posted 2020-12-12 randy-lo

题目链接：https://www.acwing.com/problem/content/200/

求解[1,N]之间的最大的反素数，有性质：

这个反素数是质因数个数最多的数中最小的一个。

证明：①假设有一个数质因数个数比它多，如果在他前面，不满足反素数的定义，如果在他后面，一定可以找到第一个质因数比它大的数，这个数作为结果更好，反证可知，这个数质因数一定是最多的

，②反证：假设有质因数与他的个数一样但是比他小，那么一定有g(i)>=g(m)，与反素数的定义矛盾。故这个数是质因数个数最多的一个数中最小的一个。

可以证明这个数一定是又连续的素数构成，且质数非严格单调减，通过交换质因子即可证明。且最多有九个质因子。

代码：

#include<iostream>
using namespace std;
int n;
typedef long long ll;
int prime[]={2,3,5,7,11,13,17,19,23,29};
ll maxx;
ll ans;
ll c[20];//指数 
void dfs(ll now,ll last,ll sum,ll prod){
    if(now==10){//搜索完前面十层 
        if(sum>maxx || (sum==maxx && prod<ans)){
            maxx=sum;
            ans=prod;        
        }
        return;
    }
    ll p=prod;
    for(int i=0;i<=last;i++){
        if(prod>n)return;
        c[now]=i;
        dfs(now+1,i,sum*(i+1),prod);
        prod*=prime[now];
    }
}
int main(){
    cin>>n;
    dfs(0,31,1,1);
    cout<<ans<<endl;    
}

 优化一下，其中指数为0的时候是没有贡献的，所以考虑删除这一点，还有，无效分支需要减掉，下面的代码在2000000000条件下dfs了1460次，比较高效。

 

 

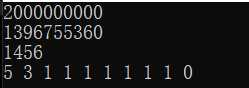
#include<iostream>
using namespace std;
typedef long long ll;
ll n;
ll prime[]={2,3,5,7,11,13,17,19,23,29};
ll maxx=0;
ll ans=0;
ll c[20];//指数 
int cnt=0;
ll final[20];
void dfs(ll now,ll last,ll sum,ll prod){
//当前搜索的数，上一次填的数，约数的个数，当前的乘积 
    cnt++;
        if(sum>maxx || (sum==maxx && prod<ans)){
            maxx=sum;
            ans=prod;
            memcpy(final,c,sizeof(c));//保存指数
        }
    for(int i=1;i<=last;i++){
        if((ll)prod*prime[now]>n)return;
        c[now]=i;    
        prod*=prime[now];
        dfs(now+1,i,sum*(i+1),prod);
    }
}
int main(){
    cin>>n;
    dfs(0,31,1,1);
    cout<<ans<<endl;    
    cout<<cnt<<endl;
    
    for(int i=0;i<10;i++)cout<<final[i]<<" ";
}