重新整理数据结构与算法——逆波兰表达计算器[八]

Posted 2020-12-11 aoximin

前言

逆波兰其实就是后缀表达式的计算。

那么就需要了解什么是前缀表达式、中缀表达式、后缀表达式。

正文

在此我就不客气了，直接复制网上的解释，基本一致我也不知道谁是原作者，就不贴出来了。

前缀表达式的计算机求值
从右至左扫描表达式
遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 op 次顶元素），并将结果入栈
重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果
示例：
计算前缀表达式的值：- + 1 × + 2 3 4 5
从右至左扫描，将5，4，3，2压入堆栈；
2）遇到+运算符，弹出2和3（2为栈顶元素，3为次顶元素），计算2+3的值，得到5，将5压入栈；
3）遇到×运算符，弹出5和4，计算5×4的值，得到20，将20压入栈；
4）遇到1，将1压入栈；
5）遇到+运算符，弹出1和20，计算1+20的值，得到21，将21压入栈；
6）遇到-运算符，弹出21和5，计算21-5的值，得到16为最终结果
可以看到，用计算机计算前缀表达式是非常容易的，不像计算后缀表达式需要使用正则匹配。

中缀表达式就是我们平时计算的1+1+22*5这种。

后缀表达式的计算机求值

与前缀表达式类似，只是顺序是从左至右：

从左至右扫描表达式
遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素op 栈顶元素 ），并将结果入栈
重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果

示例：
计算
计算后缀表达式的值：1 2 3 + 4 × + 5 -

1）从左至右扫描，将1，2，3压入栈；
2）遇到+运算符，3和2弹出，计算2+3的值，得到5，将5压入栈；
3）遇到4，将4压入栈
4）遇到×运算符，弹出4和5，计算5×4的值，得到20，将20压入栈；
5）遇到+运算符，弹出20和1，计算1+20的值，得到21，将21压入栈；
6）遇到5，将5压入栈；
7）遇到-运算符，弹出5和21，计算21-5的值，得到16为最终结果

其中逆波兰表达式其实就是后缀表达式。

那么问题来了，我们如果将中缀表达式转换为后缀表达式呢?

步骤:

1. 中缀表达式转换为前缀表达式

2. 前缀表达式转换为后缀表达式

然后就是进行计算了，比较简单哈。

好的，那么开始吧。

第一步将将string 转换为list。

static void Main(string[] args)
{
   var s = "1+((20+3)×4)-5";
   List<string> list = toInfixExpressionList(s);
	list.ForEach(u =>
	{
		Console.WriteLine(u);
	});
	Console.ReadKey();
}
/// <summary>
/// 将字符串分解为一个list
/// </summary>
/// <param name="s"></param>
/// <returns></returns>
public static List<string> toInfixExpressionList(string s)
{
	List<string> ls = new List<string>();
	int i = 0;
	char c;
	do
	{
		c = s[i];
		//判断是否为符号
		if (c < 48 || c > 57)
		{
			ls.Add(c+"");
			i++;
		}
		else
		{
			String temp= "";
			while (i <s.Length && (c = s[i]) >=48&& (c = s[i]) <= 57)
			{
				temp += c;
				i++;
			}
			ls.Add(temp);
		}
	} while (s.Length > i);
	return ls;
}

第二步去除括号转成前缀:

public static List<String> parseSuffixExpreesionList(List<String> ls)
{
	Stack<string> symbolStack = new Stack<string>();
	List<string> globalStack = new List<string>();
	Regex regex = new Regex(@"d+");
	foreach (var item in ls) {
		//匹配是否是数字
		if (regex.Match(item).Success)
		{
			globalStack.Add(item);
		}
		else if (item.Equals("("))
		{
			symbolStack.Push(item);
		}
		else if (item.Equals(")"))
		{
			while (!symbolStack.Peek().Equals("("))
			{
				globalStack.Add(symbolStack.Pop());
			}
			//弹出(符号
			symbolStack.Pop();
		}
		else
		{
			while (symbolStack.Count!=0 && Operation.getValue(item)<=Operation.getValue(symbolStack.Peek()))
			{
				globalStack.Add(symbolStack.Pop());
			}
			symbolStack.Push(item);
		}
	}
	while (symbolStack.Count != 0)
	{
		globalStack.Add(symbolStack.Pop());
	}
	return globalStack;
}

第三步进行后缀计算:

public static int calculate(List<String> ls)
{
	Stack<string> stack = new Stack<string>();
	Regex regex = new Regex(@"d+");
	foreach (var item in ls)
	{
		if (regex.Match(item).Success)
		{
			stack.Push(item);
		}
		else
		{
			int num2 = Convert.ToInt32(stack.Pop());
			int num1 = Convert.ToInt32(stack.Pop());
			int res = 0;
			if (item.Equals("+"))
			{
				res = num1 + num2;
			}
			else if (item.Equals("-"))
			{
				res = num1 - num2;
			}
			else if (item.Equals("*"))
			{
				res = num1 * num2;
			}
			else if (item.Equals("/"))
			{
				res = num1 / num2;
			}
			else
			{
				throw new Exception("运算符有误");
			}
			stack.Push("" + res);
		}
	}
	return Convert.ToInt32(stack.Pop());
}

测试

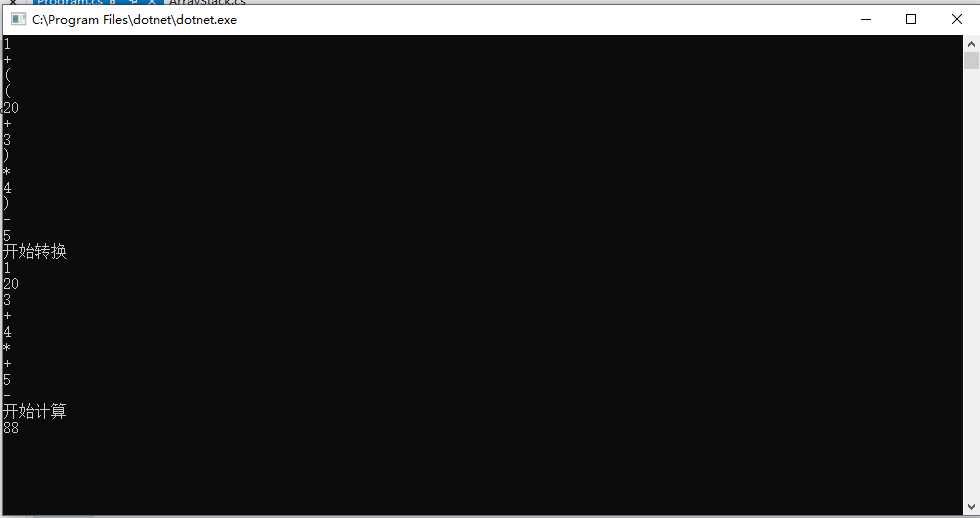
static void Main(string[] args)
{
   var s = "1+((20+3)*4)-5";
   List<string> list = toInfixExpressionList(s);
	list.ForEach(u =>
	{
		Console.WriteLine(u);
	});
	Console.WriteLine("开始转换");
	list= parseSuffixExpreesionList(list);
	list.ForEach(u =>
	{
		Console.WriteLine(u);
	});
	Console.WriteLine("开始计算");
	int result= calculate(list);
	Console.WriteLine(result);
	Console.ReadKey();
}

结果: