（C语言中）逆波兰算法（及计算器）
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了（C语言中）逆波兰算法（及计算器）相关的知识，希望对你有一定的参考价值。
Q.1: 用reverse Polish notation 表示12+3 是否是 "123+" ? 如果是， 不是和1 + 23的表示 相冲? （为了防止相冲，各个数字间是否需要特定符号隔开？）
Q.2: （Q.1 得到答复后再问）
非常感谢！
12+3应该表达为12 3+。（实际无空格，为了好看）
先解决一个问题，就是123+会不会认为是1和23或者1和2和3，其实是不会的。一般后缀式都是用栈存储的，你在定义栈的时候里面的elemtype e（当然也可以用别的就是举例），这个elemtype是重命名的int。scanf或者cin输入的时候，你先输入12，这个就被存在栈的第一空里面（因为是%d嘛），再输入3就被存在第二空里面了。这个不会混淆。
逆波兰算法是这么工作的：在后缀式中扫描，可能会扫描到一堆数字，但是这时候如果扫描到了一个运算符（加减乘除等），这时候提取运算符并提取运算符前面紧挨着的那两个数字（注意是紧挨），然后这两个数字和这一个运算符进行运算。比如123+，扫描得12，扫描得3，扫描得+（电脑得到了+这个运算符），紧接着取前面紧挨的12和3,进行运算，就是12+3了。如(2+1) * 3就是21+3*。扫描得2，扫描得1，扫描得+，ok这时候2+1=3,3入栈，重新while扫描。扫描得3（刚才算出来刚入栈的那个），扫描得3，扫描得*，ok这时候3*3=9。
1+23这种后缀式是表达不出来的。后缀它的意义就在于两个数，他们的运算符关系紧挨在他们后面。这个1+只有一个数，还原算是就是+1，无意义。 参考技术A a+b ---> a,b,+
a+(b-c) ---> a,b,c,-,+
a+(b-c)*d ---> a,b,c,-,d,*,+
a+d*(b-c)--->a,d,b,c,-,*,+
a=1+3 ---> a=1,3 +
它的优势在于只用两种简单操作，入栈和出栈就可以搞定任何普通表达式的运算。其运算方式如下：
如果当前字符为变量或者为数字，则压栈，如果是运算符，则将栈顶两个元素弹出作相应运算，结果再入栈，最后当表达式扫描完后，栈里的就是结果。本回答被提问者采纳 参考技术B 我是来围观的
算法表达式求值--逆波兰算法介绍
逆波兰算法介绍
假定给定一个只 包含 加、减、乘、除，和括号的算术表达式，你怎么编写程序计算出其结果？
问题是：在表达式中，括号，以及括号的多层嵌套 的使用，运算符的优先级不同等因素，使得一个算术表达式在计算时，运算顺序往往因表达式的内容而定，不具规律性。 这样很难编写出统一的计算指令。
使用逆波兰算法可以轻松解决这个问题。他的核心思想是将普通的中缀表达式转换为后缀表达式。
什么是中缀表达式？例如a+b，运算符在两个操作数的中间。这是我们从小学开始学习数学就一直使用的表达式形式。
什么是后缀表达式？例如a b + ，运算符在两个操作数的后面。后缀表达式虽然看起来奇怪，不利于人阅读，但利于计算机处理。
转换为后缀表达式的好处是：
1、去除原来表达式中的括号，因为括号只指示运算顺序，不是实际参与计算的元素。
2、使得运算顺序有规律可寻，计算机能编写出代码完成计算。
算术表达式的组成部分
一个表达式有如下及部分元素组成
- 操作数：可以是任何数值：1，89 ， 3.14159 ...
- 运算符：
分为单目运算符 如 sin , cos ， 双目运算符 如 加、减、乘、除 。
运算符还会分为左结合性和右结合性。同级的左结合性的运算符从左往右依次计算。同级的右结合性的运算符从右往左依次计算。
如: 7-6+1 等价于 (7-6) + 1 ，因为普通加减运算符是左结合性的。
如：C语言中的组合赋值语句： a = b = 1 等价于 a = (b=1) ，因为赋值运算符在C中是右结合性的。
对于单目运算符，还分为前缀运算符和后缀运算符，如 sin(x) 是前缀运算符，而 阶乘运算符 ： n ! 就是后缀运算符。
- 分界符：一般是圆括号 ( ) ， 用于指示运算的先后顺序。
在本文中，只会考虑算术表达式 有 加、减、乘、除 运算符， 左右圆括号 ( ， ) ，以及合法的数字简单的情况。对于更加复杂的运算符，只要对这个算法轻微修改，就可以支持。
逆波兰算法的原理
逆波兰算法的核心步骤就2个：
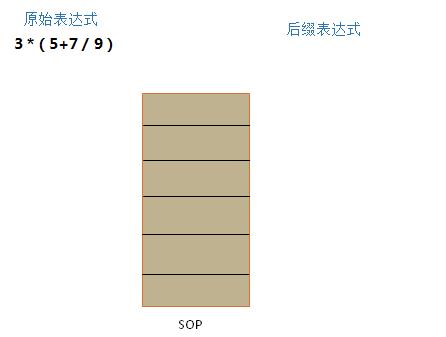
1、将中缀表达式转换为后缀表达式，例如输入的原始表达式是 3*（5+7） ，转换得到 3 5 7 + *
2、根据后缀表达式，按照特定的计算规则得到最终计算结果
下面详细介绍这个2步的操作。
中缀表达式转换为后缀表达式
你需要设定一个栈SOP,和一个线性表 L 。SOP用于临时存储运算符和左括号分界符( ，L用于存储后缀表达式。
遍历原始表达式中的每一个表达式元素
（1）如果是操作数，则直接追加到 L中。只有 运算符 或者 分界符（ 才可以存放到 栈SOP中
（2）如果是分界符
Ⅰ 如果是左括号 ( ， 则 直接压入SOP，等待下一个最近的 右括号 与之配对。
Ⅱ 如果是右括号），则说明有一对括号已经配对(在表达式输入无误的情况下)。不将它压栈，丢弃它，然后从SOP中出栈，得到元素e，将e依次追加到L里。一直循环，直到出栈元素e 是 左括号 ( ，同样丢弃他。
（3）如果是运算符（用op1表示）
Ⅰ如果SOP栈顶元素（用op2表示） 不是运算符，则二者没有可比性，则直接将此运算符op1压栈。 例如栈顶是左括号 ( ，或者栈为空。
Ⅱ 如果SOP栈顶元素（用op2表示） 是运算符 ，则比较op1和 op2的优先级。如果op1 > op2 ，则直接将此运算符op1压栈。
如果不满足op1 > op2，则将op2出栈，并追加到L，再试图将op1压栈，如果如果依然不满足 op1>新的栈顶op2，继续将新的op2弹出追加到L ，直到op1可以压入栈中为止。
也就是说，如果在SOP栈中，有2个相邻的元素都是运算符，则他们必须满足：下层运算符的优先级一定小于上层元素的优先级，才能相邻。
最后，如果SOP中还有元素，则依次弹出追加到L后，就得到了后缀表达式。
伪代码
#将参数中缀表达式expression转为后缀表达式存放在L中，返回L function infixToSuffix(expression): { for each element in expression #对表达式中的每一个元素 { if (element 是一个操作数) { L.append(element) #将这个元素追加到线性表L后 } else if (element 是 一个运算符) { While (sop栈 不为空 && sop栈顶元素 是一个运算符 && element的优先级 <= sop栈顶运算符元素的优先级 ) { L.append(sop.pop()) } sop.push(element); } else if(element 是 一个分界符) { if (element is \'(\' ) { sop.push(element) } else if( element is \')\' ) { While (sop栈不为空 && sop栈顶元素 不是 \'(\' ) #将匹配的2个括号之间的栈元素弹出，追加到L { L.append( sop.pop() ); } if(sop栈不为空 ) { sop.pop() #将匹配到的 \'(\' 弹出丢弃 } } } } While (sop 栈 不为空) #将sop栈中剩余的所有元素弹出，追加到L后 { L.append(sop.pop()) } return L }
示例图
根据后缀表达式计算得到最终结果
执行这步操作时，也需要一个栈scalc，用于存放计算中的操作数。
伪代码
function suffixToResult(suffix_expression) { for each element in suffix_expression { if(element 是 操作数) { scalc.push(element) } else if(element 是运算符) { #从栈中弹出2个操作数 num1 和 num2 。注意：后弹出的num2是第一操作数，num1是第二操作数 。 #因为这里考虑的都是二元运算符，因此需要弹2个元素出来进行运算。 num1 = scalc.pop() num2 = scalc.pop() #使用element代表的运算符完成 num2 和 num1 的计算，产生临时结果 temp_value temp_value = num2 【element的运算符: + ,- ,* , / 】 num1 #将temp_value压栈 scalc.push(temp_value) } #如果一切正常，最后栈scalc中仅仅只有一个元素，这个元素就是最终的结果 return sclac.pop() } }
示例图
代码实现（Java）
1、核心算法实现是 InfixExpression类中的 public SuffixExpression toSuffixExpression() 和 SuffixExpression 类中的 double getResultValue() throws Exception 。
2、并没有实现解析输入的代码，因此算术表达式只能通过硬编码构造。涉及到编译原理的知识，书到用时方恨少，哎。
3、所有的操作数内部使用double存储。
package com. lulix86 .calc ; import java. util .ArrayList ; import java. util .Deque ; import java. util .HashMap ; import java. util .Iterator ; import java. util .LinkedList ; import java. util .List ; import java. util .Map ; import java. util .regex . Matcher; import java. util .regex . Pattern; public class App { public static void main (String [] args ) { InfixExpression expression = new InfixExpression () ; // (1+8)-(3*(4-1)) = 0 expression .append ( "(") ; expression .append ( "1") ; expression .append ( "+") ; expression .append ( "8") ; expression .append ( ")") ; expression .append ( "-") ; expression .append ( "(") ; expression .append ( "3") ; expression .append ( "*") ; expression .append ( "(") ; expression .append ( "4") ; expression .append ( "-") ; expression .append ( "1") ; expression .append ( ")") ; expression .append ( ")") ; System . out. println( "原始表达式:" + expression ); try { System . out. println( "计算结果是:" + expression. getResultValue () ) ; } catch (Exception e) { System . out. println( "一定是表达式输入的有问题，请检查后重试" ) ; } } } /** * 表达式元素的公父类。表达式元素具体分为：运算符类，操作数类，分界符类。因此这个类有3个子类。 这是一个抽象类。 这个类的作用如下： * 1、定义了表达式元素的共同属性：String content，用来存储元素的字符串形式的内容。 * 2、限定了分界符元素和运算符元素的相关性质：如可取的content值，运算符的优先级等。 * 2、这个类提供了一些供子类使用的工具函数：isLegalXXXX。 * * * @see ExpressionDelimeter * @see ExpressionOperator * @see ExpressionOperand * */ abstract class ExpressionElement { // -----------------------------分界符----------------------------------- // 表达式中的分界符：左右圆括号 public static final String LEFT_PARENTHESES = "(" ; public static final String RIGHT_PARENTHESES = ")" ; protected static boolean isLegalDelimeter (String content) { if ( LEFT_PARENTHESES .equals ( content) || RIGHT_PARENTHESES . equals( content )) return true ; return false ; } // -----------------------------运算符----------------------------------- // 运算符:这里只用到了常见的这4个运算符 public static final String PLUS = "+" ; public static final String MINUS = "-" ; public static final String MULTIPLE = "*" ; public static final String DIVIDE = "/" ; // 将运算符 和 他的 优先级 通过 k-v 对存放到 Map中：运算符的优先级分为2个等级，用数字1 和2代表，数值越大，优先级越高 protected static final Map <String , Integer> operatorPiority = new HashMap <> (); static { operatorPiority .put ( PLUS, 1) ; operatorPiority .put ( MINUS, 1) ; operatorPiority .put ( MULTIPLE, 2) ; operatorPiority .put ( DIVIDE, 2) ; } protected static boolean isLegalOperator (String content) { if ( ! operatorPiority. containsKey (content )) return false ; return true ; } // -----------------------------操作数----------------------------------- // 通过正则表达式校验一个字符串是否是合法的数字 。 protected static boolean isLegalOperand (String content) { Pattern numberPat = Pattern .compile ( "(\\\\+|-)?(\\\\d+\\\\.)?\\\\d+" ); Matcher mat = numberPat .matcher ( content) ; if ( ! mat. matches ()) return false ; return true ; } protected final String content ; protected ExpressionElement ( String content ) { this .content = content ; } public String getContent() { return content ; } @Override public String toString() { return content . toString() ; } } /** * 表达式运算符类。 构造函数私有，不可以自己创建实例，只能用类中预定义的4个静态类对象，分别代表了加减乘除4个运算符。 类对象不可变。 * 实现了Comparable接口，compareTo方法用来比较2个运算符的优先级。 * */ class ExpressionOperator extends ExpressionElement implements Comparable <ExpressionOperator > { public static final ExpressionOperator OP_MINUS = new ExpressionOperator (ExpressionElement . MINUS) ; public static final ExpressionOperator OP_PLUS = new ExpressionOperator (ExpressionElement . PLUS) ; public static final ExpressionOperator OP_MULTIPLE = new ExpressionOperator (ExpressionElement . MULTIPLE) ; public static final ExpressionOperator OP_DEVIDE = new ExpressionOperator (ExpressionElement . DIVIDE) ; // ----------------------------------------------------- private final int priority ; // 运算符的优先级 // 不可以在类外实例化运算符，不允许创建其它的新的运算符 private ExpressionOperator ( String content ) { super (content ) ; if ( ! isLegalOperator( content )) throw new IllegalArgumentException( "运算符 " + content + " 不是合法的" ); this .priority = operatorPiority .get ( content) ; } public int getPriority() { return priority ; } @Override public int compareTo( ExpressionOperator other ) { return this . priority - other . priority; } @Override public boolean equals( Object obj ) { if ( obj == null) return false ; if ( obj == this) return true ; if ( obj .getClass () != this. getClass ()) return false ; ExpressionOperator other = ( ExpressionOperator) obj; return this . getContent() . equals( other .getContent ()) ; } } /** * 表达式操作数类。 * * 使用double作为数字的存储类型。 不可变类型。 实现了Comparable接口，compareTo方法用来比较2个操作数的大小。 * * 因为操作数是不可枚举的，因此这个类可以创建实例。 */ class ExpressionOperand extends ExpressionElement implements Comparable <ExpressionOperand > { private final double value ; public ExpressionOperand ( String content ) { super (content ) ; try { value = Double. parseDouble (content ) ; } catch (NumberFormatException e) { throw new IllegalArgumentException( content + " 不是一个合法的数字" ); } } public ExpressionOperand ( double value ) { super (Double . toString( value )); this .value = value ; } public double getValue() { return value ; } @Override public int compareTo( ExpressionOperand other ) { return Double . compare( this .value , other . value) ; } @Override public String toString() { return Double . toString( this .value ) ; } } /** * 表达式分界符类。 不可变类型。 构造函数私有，不可以自己创建实例，只能用类中预定义的2个静态类对象，分别代表左，右括号。 * */ class ExpressionDelimeter extends ExpressionElement { public static final ExpressionDelimeter DM_LEFT_PARENTHESES = new ExpressionDelimeter ( ExpressionElement . LEFT_PARENTHESES) ; public static final ExpressionDelimeter DM_RIGHT_PARENTHESES = new ExpressionDelimeter ( ExpressionElement . RIGHT_PARENTHESES) ; private ExpressionDelimeter ( String content ) { super (content ) ; if ( ! isLegalDelimeter( content )) throw new IllegalArgumentException( "分界符 " + content + " 不是合法的" ); } @Override public boolean equals( Object obj ) { if ( obj == null) return false ; if ( obj == this) return true ; if ( obj .getClass () != this. getClass ()) return false ; ExpressionDelimeter other = ( ExpressionDelimeter) obj ; return content . equals( other .content ) ; } } /** * 表达式类。 你可以把这个类看做是一个存储表达式元素的线性表，因此可以使用appendXXX方法来构造一个表达式。 * * 封装了工具函数 infixToSuffix，用于将中缀表达式转换为后缀表达式。 * 实现了 Iterable接口，可以迭代ExpressionElement元素对象。 */ abstract class Expression implements Iterable< ExpressionElement > { // --------------------------------------------------------------------------- // 使用ArrayList存储表达式元素 protected final List< ExpressionElement > expression = new ArrayList <>() ; // 追加一个表达式元素对象，不可以追加空元素。 public boolean append( ExpressionElement e ) { if ( e == null) return false ; expression .add ( e) ; return true ; } public boolean append( String content ) { switch ( content ) { case ExpressionElement . LEFT_PARENTHESES: expression .add ( ExpressionDelimeter. DM_LEFT_PARENTHESES ) ; break ; case ExpressionElement . RIGHT_PARENTHESES: expression .add ( ExpressionDelimeter. DM_RIGHT_PARENTHESES ) ; break ; case ExpressionElement . PLUS: expression .add ( ExpressionOperator. OP_PLUS ); break ; case ExpressionElement . MINUS: expression .add ( ExpressionOperator. OP_MINUS ); break ; case ExpressionElement . MULTIPLE: expression .add ( ExpressionOperator. OP_MULTIPLE ); break ; case ExpressionElement . DIVIDE: expression .add ( ExpressionOperator. OP_DEVIDE ); break ; default : try { ExpressionOperand operand = new ExpressionOperand (content ) ; // 构造时使用了parseDouble expression .add ( operand) ; } catch (Exception e) { return false ; } } return true ; } @Override public String toString() { boolean firstAdd = true ; StringBuilder sb = new StringBuilder () ; for ( ExpressionElement e : expression ) { if ( ! firstAdd) { sb .append ( " ") ; } else { firstAdd = false; } sb .append ( e. toString ()); } return sb . toString() ; } @Override public Iterator < ExpressionElement> iterator() { return expression . iterator() ; } public void clear() { this .expression . clear() ; } // 获取表达式最终的运算的结果 public abstract double getResultValue() throws Exception ; } class SuffixExpression extends Expression { private double doPlus( ExpressionOperand a , ExpressionOperand b ) { return a . getValue() + b .getValue () ; } private double doMinus( ExpressionOperand a , ExpressionOperand b ) { return a . getValue() - b .getValue () ; } private double doMultiple( ExpressionOperand a , ExpressionOperand b ) { return a . getValue() * b .getValue () ; } private double doDevide( ExpressionOperand a , ExpressionOperand b ) { return a . getValue() / b .getValue () ; } // SuffixExpression 本身已经是一个后缀表达了。getResultValue计算出结果就OK了 @Override public double getResultValue () throws Exception { SimpleStack <ExpressionOperand > scalc = new SimpleStack <>() ; for ( ExpressionElement e : expression ) { if ( e instanceof ExpressionOperand) { scalc .push (( ExpressionOperand) e) ; } else if ( e instanceof ExpressionOperator ) { ExpressionOperator operator = ( ExpressionOperator) e; // 获取这个运算符 ExpressionOperand opf = scalc .pop () ; // 弹出二元运算符的第二个操作数 ExpressionOperand ops = scalc .pop () ; // 弹出二元运算符的第一个操作数 ExpressionOperand temp = null ; // 存储临时运算结果 if ( opf == null || ops == null ) throw new Exception( "表达式不合法，不能完成计算" ) ; if ( operator. equals (ExpressionOperator . OP_PLUS)) { temp = new ExpressionOperand (doPlus ( ops, opf)) ; } else if ( operator. equals (ExpressionOperator . OP_MINUS)) { temp = new ExpressionOperand (doMinus ( ops, opf)) ; } else if ( operator. equals (ExpressionOperator . OP_MULTIPLE)) { temp = new ExpressionOperand (doMultiple ( ops, opf)) ; } else if ( operator. equals (ExpressionOperator . OP_DEVIDE)) { temp = new ExpressionOperand (doDevide ( ops, opf)) ; } scalc .push ( temp) ; } // else if } // end foreach if ( scalc .size () != 1) throw new Exception( "表达式不合法，不能完成计算" ) ; // 从 scalc栈中取出最后一个元素就是结果 return scalc . pop() . getValue() ; } } class InfixExpression extends Expression { public SuffixExpression toSuffixExpression() { SuffixExpression suffix = new SuffixExpression () ; // suffix是一个用来存储表达式元素的线性表对象，对应算法中的L SimpleStack <ExpressionElement > sop = new SimpleStack <>() ; // sop 栈 // 遍历原始表达式中的每一个元素 for ( ExpressionElement e : expression ) { if ( e instanceof ExpressionOperand) // 如果是操作数，则直接追加到后缀表达式suffix中 { suffix .append ( e) ; } else if ( e instanceof ExpressionDelimeter ) // 如果是分界符 { if ( e. equals (ExpressionDelimeter . DM_LEFT_PARENTHESES )) // 是 左括号,则直接压栈 { sop .push ( e) ; } else if ( e. equals (ExpressionDelimeter . DM_RIGHT_PARENTHESES )) // 是 右括号，则从 sop中弹出与这个括号配对的中间的所有元素， { // 并追加到后缀表达式中 while ( ! sop. isEmpty () && ! sop. peek (). equals (ExpressionDelimeter . DM_LEFT_PARENTHESES )) { suffix .append ( sop. pop ()); // 将元素出栈，追加到 suffix 表中去 } if ( ! sop. isEmpty ()) { sop .pop () ; // 将栈顶的( 出栈，丢弃。 } } } else if ( e instanceof ExpressionOperator ) // 如果是运算符 { while ( ! sop. isEmpty () && sop . peek() instanceof ExpressionOperator && 0 >= (( ExpressionOperator) e ). compareTo ((ExpressionOperator ) sop . peek())) { suffix .append ( sop. pop ()); } sop .push ( e) ; } } // end of foreach // 将 sop栈中剩余的元素全部追加到suffix后 while ( ! sop. isEmpty ()) { suffix .append ( sop. pop ()); } return suffix ; } @Override public double getResultValue () throws Exception { return toSuffixExpression () .getResultValue () ; } } /** * * 因为Java集合框架中的Stack类是线程安全的， 但是这里不需要这种特性，为了提高效率，使用双端队列作为内部实现，自己封装成为一个栈数据结构。 * * @see java.util.Stack <E> * @see java.util.Deque <E> * @see java.util.LinkedList <E> */ class SimpleStack < E> { private final Deque< E > deque = new LinkedList < E> (); public E pop() { return deque . pop() ; // 双端队列的第一个元素，也就是栈的栈顶 } public E peek() { return deque . peek() ; } public void push( E e ) { deque .push ( e) ; // 压栈 } public int size() { return deque . size() ; } public boolean isEmpty() { return 0 == deque .size () ; } @Override public String toString() { StringBuilder sb = new StringBuilder () ; sb .append ( "栈顶[") ; for ( E e : deque) { sb .append ( e. toString () + "," ) ; } sb .append ( "]栈底") ; return sb. toString (); } }
以上是关于（C语言中）逆波兰算法（及计算器）的主要内容，如果未能解决你的问题，请参考以下文章