[P4980] 模板Polya定理 - Polya定理,欧拉函数

Posted 2020-12-10 mollnn

Description

求 (n) 元环的 (n) 染色方案数，旋转同构，翻转不同构，颜色可以不用完。

Solution

根据 Polya 定理得出计算式，然后就是非常套路的推导了。

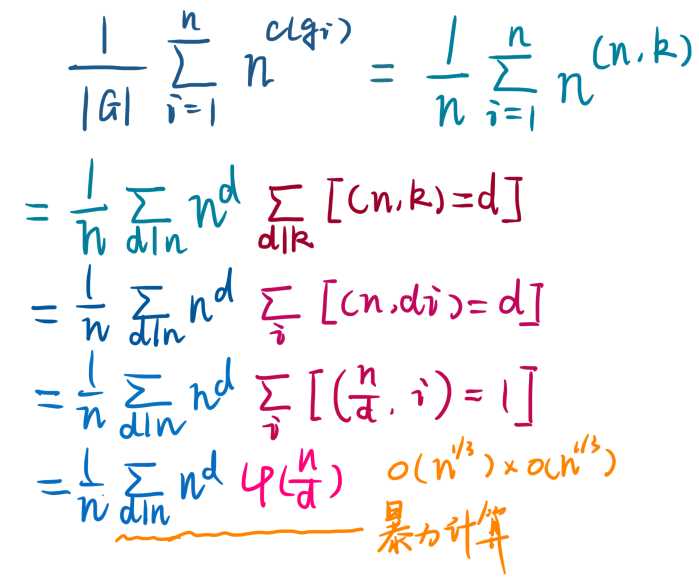
对于欧拉函数，暴力计算即可

#include <bits/stdc++.h>

using namespace std;

#define int long long
const int N = 1000005;
const int mod = 1e+9+7;

namespace prime {
    const int MAXN = 1000005;
    bool isNotPrime[MAXN + 1];
    int mu[MAXN + 1], phi[MAXN + 1], primes[MAXN + 1], cnt, a[N];
    inline void euler() {
        isNotPrime[0] = isNotPrime[1] = true;
        mu[1] = 1;
        for (int i = 2; i <= MAXN; i++) {
            if (!isNotPrime[i]) {
                primes[++cnt] = i;
                mu[i] = -1;
            }
            for (int j = 1; j <= cnt; j++) {
                int t = i * primes[j];
                if (t > MAXN) break;
                isNotPrime[t] = true;
                if (i % primes[j] == 0) {
                    mu[t] = 0;
                    break;
                } else {
                    mu[t] = -mu[i];
                }
            }
        }
        for(int i=1;i<=cnt;i++) {
            int p=primes[i];
            for(int j=1;p*j<N;j++) {
                a[p*j]+=mu[j];
            }
        }
        for(int i=1;i<N;i++) {
            a[i]+=a[i-1];
        }
    }
}

int phi(int n) {
    int ans=n,t=n;
    for(int i=2;i*i<=n;i++) {
        if(n%i==0 && !prime::isNotPrime[i]) {
            ans=ans/i*(i-1);
            while(t%i==0) t/=i;
        }
    }
    if(t>1) ans=ans/t*(t-1);
    return ans;
}

int qpow(int p,int q) {return (q&1?p:1)*(q?qpow(p*p%mod,q/2):1)%mod;}
int inv(int p) {return qpow(p,mod-2);}

int solve(int n) {
    int ans=0;
    for(int i=1;i*i<=n;i++) {
        if(n%i==0) {
            ans+=qpow(n,i)*phi(n/i)%mod;
            if(i*i!=n) ans+=qpow(n,n/i)*phi(i)%mod;
            ans%=mod;
        }
    }
    ans*=inv(n);
    ans%=mod;
    return ans;
}

signed main() {
    int t,n;
    ios::sync_with_stdio(false);
    prime::euler();
    cin>>t;
    while(t--) {
        cin>>n;
        cout<<solve(n)<<endl;
    }
}