最长公共子串和最长公共子序列(LCS问题)

Posted 2020-12-07 yangfei629

一、区别

---

给定两个字符串，求LCS

 

最长公共子串 （Longest Common Substring）： 要求是连续的字符串

最长公共子序列（Longest Common Subsequence）：要求子字符串相对顺序不变即可

 

二、动态规划求解

---

 

1、最长公共子串

      给定两个字符串A 和 B

      用二维数组 d[i][j] 表示 A的前i个字符串-B的前j个字符串 的最长公共子串长度

     d[i][j] = d[i-1][j-1] + 1 （A[i] == B[j]）

                 0                     (A[i] != B[j])  (注意此处为了求解子串 返回0，而不是Max(d[i-1][j], d[i][j-1]))

    例 如下， 取最大值=2

      

 

    

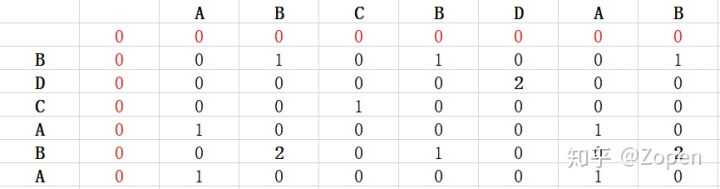
      此时列出最长公共子串，如下找出最大的值2，向左上角递进，直到值=1

     则找出最长公共子串 AB BD AB

 

 

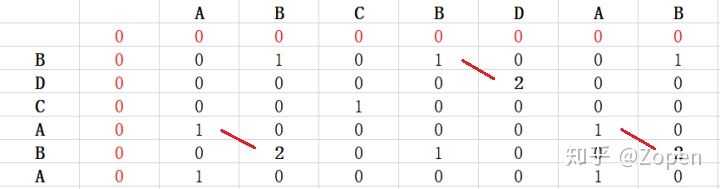
2、最长公共子序列

 

     d[i][j] = d[i-1][j-1] + 1 （A[i] == B[j]）

                 Max(d[i-1][j], d[i][j-1])

    

     最长公共子序列必然==右下角的值==4

 

 

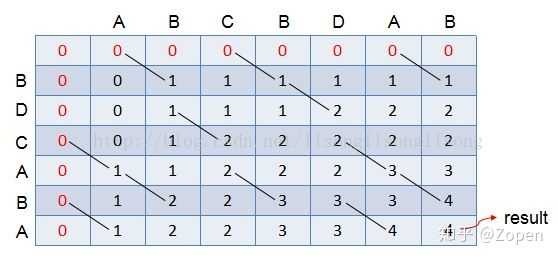
   列出所有的最长公共子序列：

        从右下角开始计算

 

1. 如果d[i][j]对应的A[i-1] == B[j-1]，则把这个字符放入 LCS 中，并跳入d[i-1][j-1]中继续进行判断；
2. 如果格子d[i][j]对应的 A[i-1] ≠ B[j-1]，则比较d[i-1][j]和d[i][j-1]的值，跳入值较大的格子继续进行判断；(此时两边相等=说明有多个结果)
3. 直到 i 或 j 小于等于零为止，倒序输出 LCS

 

 

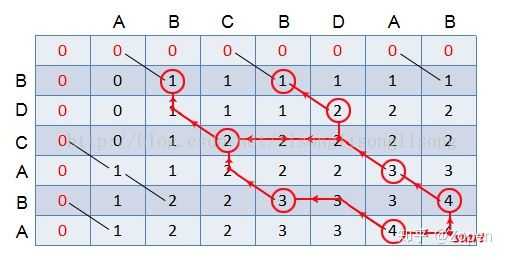
 输出：“BDAB”、“BCAB”、“BCBA”。

 递归代码：

public List<String> getLcsString(int i,int j, int[][] d) {
        List<String> lcsList = new ArrayList<>();

        if (A.indexOf(i) == B.indexOf(j)) {
            List<String> subLcsList = getLcsString(i-1,j-1,d);
            lcsList.addAll(subLcsList.stream().map(str -> str+A.indexOf(i)).collect(Collectors.toList()));
        } else if (d[i-1][j] == d[i][j-1]){
            List<String> subLcsList1 = getLcsString(i-1,j,d);
            List<String> subLcsList2 = getLcsString(i,j-1,d);
            lcsList.addAll(subLcsList1);
            lcsList.addAll(subLcsList2);
        } else if (d[i-1][j] > d[i][j-1]){
            List<String> subLcsList = getLcsString(i-1,j,d);
            lcsList.addAll(subLcsList);
        } else {
            List<String> subLcsList = getLcsString(i,j-1,d);
            lcsList.addAll(subLcsList);
        }
        return lcsList;
    }

　　

 参考：https://zhuanlan.zhihu.com/p/68409952