python数据分析-微积分基础

Posted 2023-02-21 csdn1561168266

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了python数据分析-微积分基础相关的知识，希望对你有一定的参考价值。

大家好，在这个信息化时代，数据分析在各领域中发挥着越来越重要的作用。大家使用大数据技术从海量数据中挖掘信息，发现规律，探索潜在价值。在大数据的研究和应用中，数学是坚实的理论基础。在数据预处理、分析与建模、模型评价与优化等过程中，数学方法扮演着至关重要的角色。

所以接下来，我们用python语言去实现微积分的一些基础计算等。常用第三方SymPy库来实现微积分计算。

SymPy的全称为Symbolic Python，是由纯Python语言编写的一个用于符号运算的库，能够与其他科学计算库相结合。符号化的计算采用的是数学对象符号化的计算方式，使用数学对象的精确标识，而不是近似的，计算结果可以为一个数学表达式。它的目标在于成为一个富有特色的计算机代数系统，同时保证自身的代码尽可能简单，且易于理解，容易扩展。

一、求一元二次方程

使用solve(f, *symbols, **flags)


from sympy import *#导入SymPy库
x  = symbols('x')#将x定义为符号变量
#通过SymPy库的solve()命令求得一元二次方程的两个根
x = solve(x**2-5*x+6,x)
print('一元二次方程的两个根：',x)

输出结果：

一元二次方程的两个根：[2, 3]

二、集合的运算

A = set('12345')#定义集合A
B = set('234')#定义集合B
print('集合A和集合B的并：',A|B)
print('集合A和集合B的交：',A&B)
print('集合A和集合B的差：',A-B)

输出结果：

集合A和集合B的并：'3', '4', '5', '2', '1'
集合A和集合B的交： '2', '3', '4'
集合A和集合B的差：'1', '5'

三、数列的极限

计算数列的极限，可以使用SymPy库的limit函数实现。语法格式如下：

sympy.limit(e,z,z0,dir='+')
#e：接受SymPy表达式，表示需要进行求极限的数列的一般项或函数。无默认值
#z:接受SymPy表达式，表示需要进行极限的数列的项或函数的目标值。无默认值
#z0:接受any expression,包含所有类型的数值、∞和-∞等，表示自变量趋于有限值或趋于无穷大，其中∞表示无穷大。无默认值
#dir:接受+或-。取值+时，表示趋于有限值的右极限（z→z0+）；取值-时，表示趋于有限值的左极限（z→z0-）。对于无穷大的z0(∞或-∞)，dir参数无效。默认为+

3.1 数列1/2,2/3,3/4，…,n/(n+1),...的一般项为xn=n/(n+1)，当n→∞时，判断数列｛xn｝是否收敛。

from sympy import *#导入SymPy库
n = symbols('n')#将n定义为符号变量
s = n/(n+1)
print('数列的极限为：',limit(s,n,oo))

结果输出：


数列的极限为：1

3.2 当x→-1/2时，计算函数f(x)=(1-4x^2)/(2x+1)的极限。


from sympy import *#导入SymPy库
x = symbols('x')#将x定义为符号变量
s = (1-4*x**2)/(2*x+1)
print('函数的极限：',limit(s,x,-1/2))

结果输出：


函数的极限：2.00000000000000

3.3 当x→∞时，计算函数f(x)=(1+x^3)/2x^3的极限。

from sympy import *#导入SymPy库
x = symbols('x')#将x定义为符号变量
s = (1+x**3)/(2*x**3)
print('函数的极限：',limit(s,x,oo))

结果输出：


函数的极限：1/2

四、求导数

求导数可以使用SymPy库的diff函数实现。语法格式如下：


sympy.diff(f,*symbols,**kwargs)
#f:接收SymPy表达式，表示需要进行求导的函数。无默认值
#*symbols:接收symbol，表示需要进行求导的函数的自变量。无默认值
#**kwargs:接收int，表示函数需要求导的阶数。默认为1。

4.1 求常数函数y=C（其中，C为常数）的导数。

from sympy import *
x = symbols('x')
c=2
y=c
diff(y,x)

结果输出：

4.2 求幂函数y=xμ（其中，μ是常数）的导数。


from sympy import *
x = symbols('x')#将x定义为符号变量
mu= symbols('mu')#将mu定义为符号变量
y=x**mu
init_printing()#美化输出公式
diff(y,x)

结果输出:

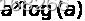
其他求导可自行验证。

五、复合函数求导法则

若y=sinx2，求dy/dx


#求复合函数的导数
from sympy import *
x = symbols('x')#将x定义为符号变量
u = symbols('u')#将u定义为符号变量
u = x**2
y = sin(u)
init_printing()#美化输出公式
diff(y,x)

结果输出：

六、微分的近似运算

需要numpy库来计算数值

6.1 求sin29的近似值。


import numpy as np
x =(29/360)*2*np.pi#假设x=29°
y=np.sin(x)
print('29°角的正弦数值为',y)

结果输出：


29°角的正弦数值为 0.48480962024633706

6.2 求1.02^(1/3)的近似值。


import numpy as np
x =1.02
y=x**(1/3)
print('1.02开3次方根的值为：',y)

结果输出：


1.02开3次方根的值为：1.006622709560113

七、微分中值

7.1 求曲线f（x）=2*x3−12*x2+18x−2的凹凸区间及拐点。


from sympy import *
x = symbols('x')#将x定义为符号变量
y =2*x**3-12*x**2+18*x-2
df1=diff(y,x)#一阶导数
df2=diff(y,x,2)#二阶导数
print('令二阶导函数为零的x取值为',solve(df2,x))#solve求解二阶导数方程的解
print('函数在拐点的值为',y.subs(x,2))#把x=2代入y中，算出拐点值

结果输出：

令二阶导函数为零的x取值为 [2]
函数在拐点的值为 2

7.2 求函数f（x）=（x+3^2*(x−1)^3的极值。

利用第一充分条件求函数的极值点

from sympy import *
x = symbols('x')#将x定义为符号变量
y = (x+3)**2*(x-1)**3
df=diff(y,x)#一阶导数
print('函数的驻点:',solve(df,x))#solve求解一阶导数方程的解
print('函数的极值为:',y.subs(x,-3),y.subs(x,-7/5),y.subs(x,1))#把x=-3代入y中，算出极值

结果输出：


函数的驻点: [-3, -7/5, 1]
函数的极值为: 0 -35.3894400000000 0

7.3 求函数f（x）=2*x^3−6*x^2+7的极值。

利用第二充分条件求函数的极值点


from sympy import *
x = symbols('x')#将x定义为符号变量
y = 2*x**3-6*x**2+7
df = diff(y,x)#一阶求导
solve(df,x)#solve求解一阶导数方程的解
print('函数的极值点:',solve(df,x))
df2 = diff(y,x,2)#二阶求导
print('二阶导数在驻点的值为：',df2.subs(x,0),df2.subs(x,2))#把x=0/2代入y中，算出极值
print('函数的极值为:',y.subs(x,0),y.subs(x,2))

结果输出：


函数的极值点: [0, 2]
二阶导数在驻点的值为：-12 12
函数的极值为: 7 -1

八、不定积分

计算连续函数的不定积分，可以使用SymPy库的integrate函数实现。语法格式如下：


sympy.integrate(f,var,…)
# f:接收SymPy表达式，表示需要进行求积分的函数，无默认值
# var:接收symbol、tuple(symbol,a,b)或several variables。symbol表示需要进行求积分的函数的一个自变量；
# tuple(symbol,a,b)用于求定积分，其中symbol表示函数的自变量，a表示积分下限，b表示积分上限；
# several variables表示指定几个变量，在这种情况下，结果是多重积分；
# 若完全不指定var,则返回f的完全反导数，将f整合到所有变量上

利用SymPy库计算不定积分时，最后的输出结果会少一个常数C，但不影响对问题的理解。

8.1 求不定积分∫cosxdx、∫1/(1+x^2)dx、∫3x^2dx。


from sympy import *
x = symbols('x')#将x定义为符号变量
f1 = cos(x)
f2 = 1/(1+x**2)
f3 = 3*x**2
init_printing()#美化输出公式
print("不定积分：",integrate(f1,x),integrate(f2,x),integrate(f3,x))

结果输出：


不定积分：sin(x) atan(x) x**3

8.2 已知某曲线上的任意一点P（x，y）处的切线斜率为该点横坐标的倒数，且该曲线过点（e2，3），求此曲线方程。


from sympy import *
x = symbols('x')#将x定义为符号变量
f = 1/x
init_printing()#美化输出公式
integrate(f,x)#求不定积分
print(integrate(f,x))

结果输出：


log(x)

九、定积分

计算定积分的关键是求被积函数的一个原函数，这里只需计算不定积分，所以，也可以使用SymPy库中的integrate函数实现定积分的计算。

计算由曲线y=x^2+1、直线x=a和x=b（a<b）及x轴围成的图形面积。

from sympy import *
x = symbols('x')#将x定义为符号变量
a = symbols('a')#将a定义为符号变量
b = symbols('b')#将b定义为符号变量
y = x**2+1
print(integrate(y,(x,a,b)))#tuple(symbol,a,b)用于求定积分，其中symbol表示函数的自变量，a表示积分下限，b表示积分上限；

结果输出：