Lindström–Gessel–Viennot lemma 应用两则
Posted haze
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Lindström–Gessel–Viennot lemma 应用两则相关的知识，希望对你有一定的参考价值。
原博客：http://www.cnblogs.com/jszkc/p/7309468.html
对于一张无边权的DAG图，给定n个起点和对应的n个终点，这n条不相交路径的方案数为
det(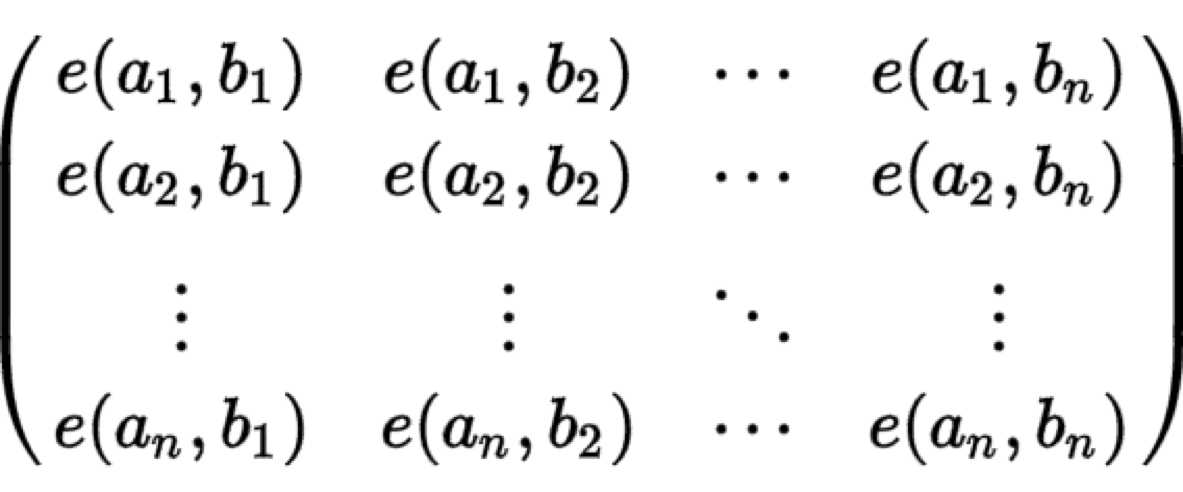
) （该矩阵的行列式）
其中e(a,b)为图上a到b的方案数
codeforces 348D
[给定一张n*m带障碍的图，求从左上角到右下角不相交两条路径的方案]
[a1=(1,2) a2=(2,1) b1=(n-1,m) b2=(n,m-1) 应用该定理即可]
HDU 5852
[给一张n*n的图，第一行m个点对应第n行的m个点，求路径不相交的方案数]
[计算对应的行列式，注意高斯消元不要T]
wiki：https://en.wikipedia.org/wiki/Lindstr%C3%B6m%E2%80%93Gessel%E2%80%93Viennot_lemma
简单来说，dag中n个起点 n个终点 矩阵a[i][j]表示第i个起点到第j个终点路径方案数，整个矩阵的行列式就是这n条线路不相交的方案数
见过一万次的格子图从左下到右上QAQ
以上是关于Lindström–Gessel–Viennot lemma 应用两则的主要内容，如果未能解决你的问题，请参考以下文章
Lindström–Gessel–Viennot lemma 应用两则
Nowcoder Monotonic Matrix ( Lindström–Gessel–Viennot lemma 定理 )