支撑向量机SVM-1.原理
Posted shuai-long
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了支撑向量机SVM-1.原理相关的知识,希望对你有一定的参考价值。
支撑向量机的英文名叫: Support Vector Machine,是机器学习领域中的很重要的一种算法。它的思想背后有极强的统计理论的支撑,也是统计学上常用的一种方法。此算法在机器学习中既能解决分类问题,又能解决回归问题。且对真实的数据具有很好的泛化能力。
原理:考虑如下样本数据集,如何分辨此数据集?
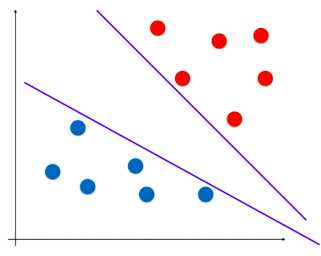
之前的逻辑回归算法,确定决策边界的思路是定义了一个概率函数,根据这个概率函数进行建模,形成了损失函数,最小化损失函数来确定决策边界。
支撑向量机和逻辑回归不同,它的实现是找到一条最优的决策边界,距离两个类别的最近的样本距离最远,如下图:
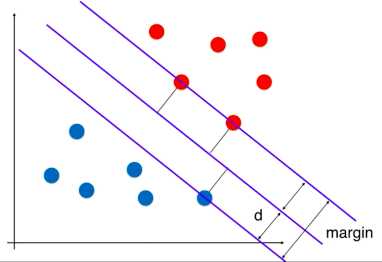
最近的点也称为支撑向量,这些支撑向量定义了一个区域,而我们找到的决策边界就是被这个区域所定义的,是位于区域中心的一条线。支撑向量机的目标就是最大化margin,即最大化d。
数学求解
回忆解析几何知识,求点到直线的距离:
点((x,y))到直线(Ax+By+C=0)的距离公式为:
[ frac{left | Ax+By+C
ight | }{sqrt{A^2+B^2}} ]
扩展到n维空间直线 ( heta ^Tcdot X_b = 0) -> (w^T cdot X +b = 0):
[frac{left | w^T cdot X +b
ight | }{left | w
ight |}]
其中(left | w
ight | = sqrt{w_1^2+w_2^2+...+w_n^2})
假设决策边界为(w^T cdot X +b = 0),对于上图中的两类样本,假设一类为1,在直线的上方,另一类为-1,在直线的下方,分别有:
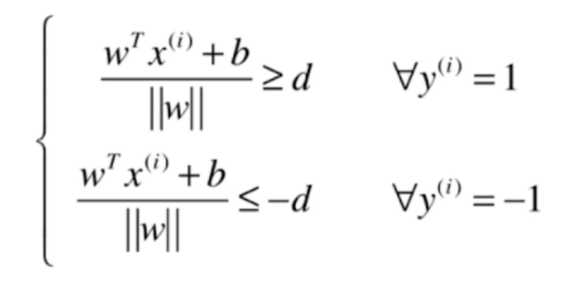
式子两边同除于d
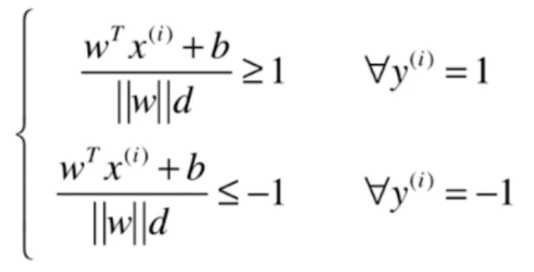
对于上式,({left | w
ight |}d)是一个常数,再化简得:
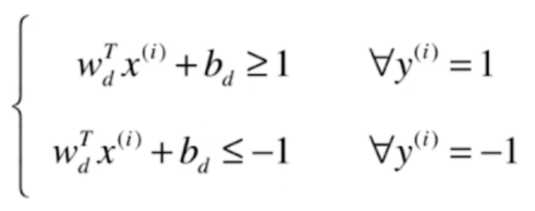
上式可合为:
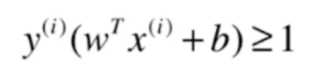
对于任意支撑向量x,d的距离应该经可能大,即要解决的是:
[max frac{left | w^T cdot X +b
ight | }{left | w
ight |}]
而又因为支撑向量构成的直线如下:
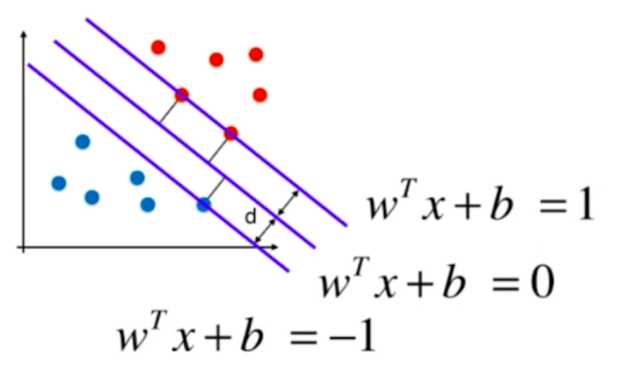
即({left | w^T cdot X +b
ight | } = 1),所以,目标函数为:(min {left | w
ight |})
为了方便求导,最终的目标为:
[min frac{1}{2}{left | w
ight |}^2
\\s.t.quad y^{(i)}(w^Tx^{(i)}+b)>1]
注:(s.t.) 为约束条件。
Soft Margin和SVM的正则化
对于数据样本如下的数据集,严格的按红蓝样本点来确定决策边界是不太准确的,因为最右边的这个蓝色点或许是一个错误的点或者是一个特殊的点,而采用另一个有容错的直线可能泛化能力会好一点。
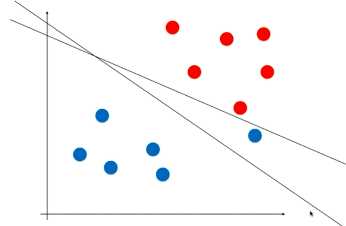
为了更好的容错,将限定条件改为:
[s.t.quad y^{(i)}(w^Tx^{(i)}+b)>1-xi _i (xi geq 0)]
但(xi)也不能无限制的大,所以在目标函数中加入正则项:
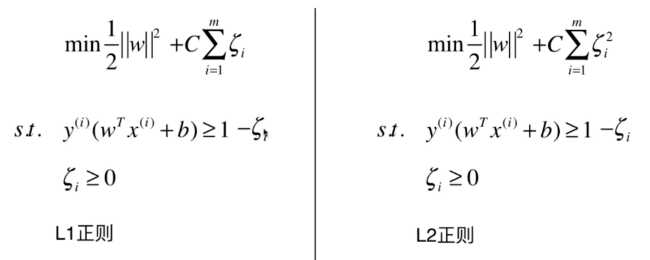
以上是关于支撑向量机SVM-1.原理的主要内容,如果未能解决你的问题,请参考以下文章