数据结构之树篇2——二叉排序(查找,搜索)树
Posted czc1999
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之树篇2——二叉排序(查找,搜索)树相关的知识,希望对你有一定的参考价值。
二叉排序树
引入
基本性质:
二叉排序树(又叫二叉搜索、查找树)
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 左、右子树也分别为二叉排序树。
- 不允许有键值相同结点。
二分查找与二叉排序树
? 二分查找也称为折半查找,要求原线性表有序,它是一种效率很高的查找方法。如果在需要进行频繁修改的表中采用二分查找,其效率也是非常低下的,因为顺序表的修改操作效率低。如果只考虑频繁的修改,我们可以采用链表。然而,链表的查找效率又非常低。综合这两种数据结构的优势,二叉查找树(Binary Sort/Search Tree)诞生了。
给定一串数((65,32,87,46,71,98,39)),使用插入构造法,步骤如下:
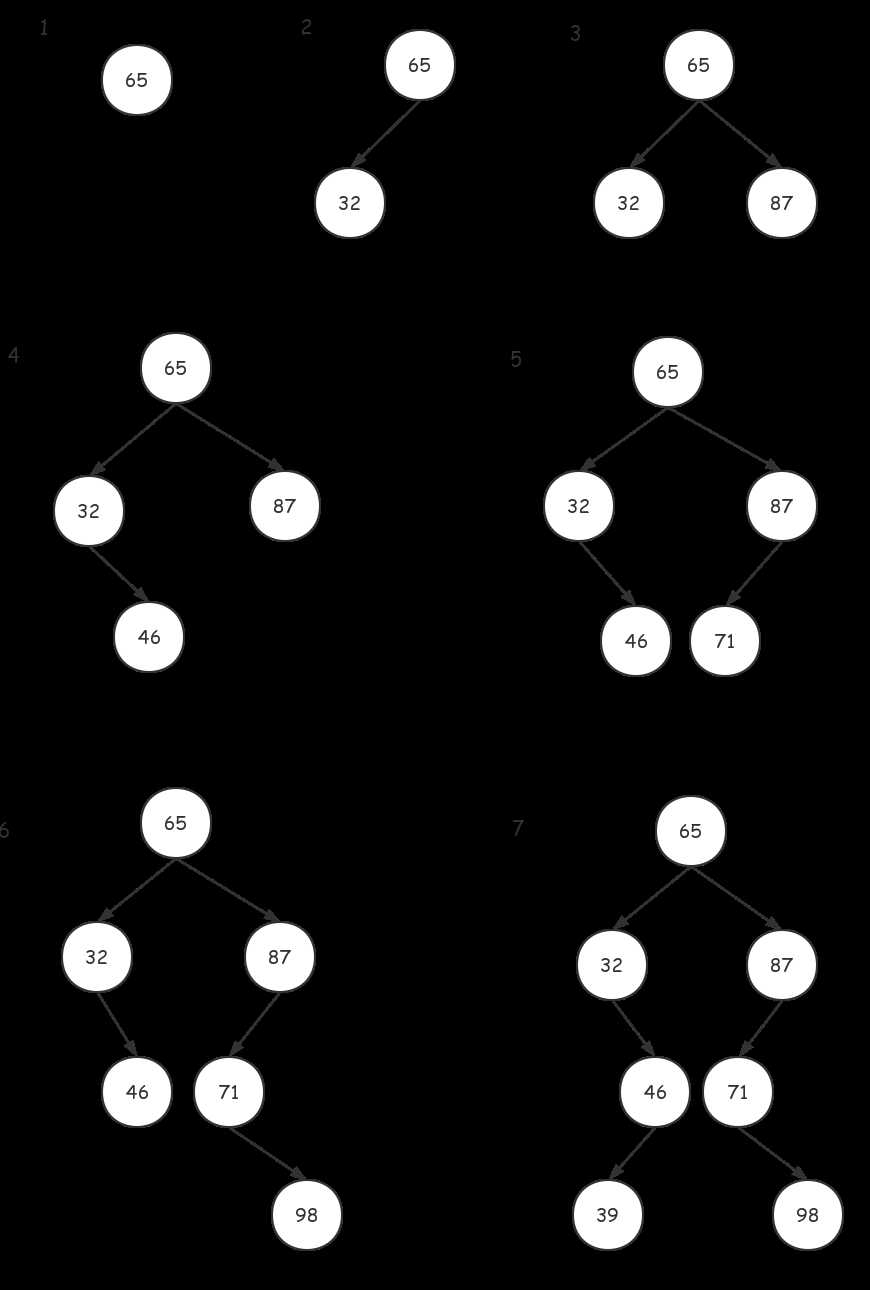
构建
非递归算法
typedef struct BinarySortTreeNode{
int data;
struct BinarySortTreeNode *Left = NULL;
struct BinarySortTreeNode *Right = NULL;
}*BinarySortTree;
BinarySortTree CreatBStree(int *a,int length) {
BinarySortTree BST = new BinarySortTreeNode;
BST->data = *a++;
for (int i = 1; i < length; i++) {
BinarySortTreeNode *pre = NULL, *p = BST, *Node=new BinarySortTreeNode;
while (p) {
pre = p;
p = *a < p->data ? p->Left : p->Right;
}
Node->data = *a;
*a < pre->data ? pre->Left = Node : pre->Right = Node;
a++;
}
return BST;
}递归写法
BinarySortTree InsertBStree(BinarySortTree BST, int x){
if (BST == NULL){
BST = new BinarySortTreeNode;
BST->data = x;
return BST;
}
if (x < BST->data)
BST->Left = InsertBStree(BST->Left, x);
else
BST->Right = InsertBStree(BST->Right, x);
return BST;
}
BinarySortTree CreatBStByRecursion(int *a,int length) {
BinarySortTree BST = NULL;
for (int i = 0; i < length; i++)
BST = InsertBStree(BST, a[i]);
return BST;
}插入与删除
插入节点
? 这个算法加个循环就可以作为 " 建立二叉排序树 " 的算法递归写法。
BinarySortTree InsertBStree(BinarySortTree BST, int x){
if (BST == NULL){
BST = new BinarySortTreeNode;
BST->data = x;
return BST;
}
if (x < BST->data)
BST->Left = InsertBStree(BST->Left, x);
else
BST->Right = InsertBStree(BST->Right, x);
return BST;
}
BinarySortTree CreatBStByRecursion(int *a,int length) {
BinarySortTree BST = NULL;
for (int i = 0; i < length; i++)
BST = InsertBStree(BST, a[i]);
return BST;
}查找节点
找不到返回NULL,找到返回该节点。
BinarySortTreeNode* BSTreeFind(BinarySortTree BST,int x) {
BinarySortTree p = BST;
while (p) {
if (x == p->data) break;
p = x > p->data ? p->Right : p->Left;
}
return p;
}删除节点
1. 被删除的结点是叶子,将父节点的 left 或 right 指针域设置为NULL。
2. 被删除的结点只有左子树或者只有右子树,用该节点的 left 或 right 重新接上来。和删除单链表节点类似。
(第一种情况,写的时候 可以和第二种合并起来)
3. 被删除的结点既有左子树,也有右子树,需要按照二叉排序树的性质从其左子树或者有子树中选择节点补到待删除节点的位置。(选左、选右都可以)
如果从左子树中选,就应该选择左子树中最右边的那个叶子节点(这里肯定是叶子,如果不是叶子,那么就不是最右边的节点)
如果从右子树中选,就应该选择右子树中最左边的那个叶子节点。
写法1 :
? 这个写法更适合JAVA之类,有垃圾回收的语言,可以把代码里的那些delete省去,但是必须要注意的是:必须这样调用 Tree = BSTDel ( Tree , delNum) ; 就像函数里面的递归一样形式,否则删除只有一个子树的根节点的时候,会出错。
//获得子树中的最大值
int GetMax(BSTree root) {
if (root->Right == NULL) return root->data;
return GetMax(root->Right);
}
//删除子树中的最大值
BSTree DelMax(BSTree root) {
if (root->Right == NULL) {
BSTNode *t= root->Left;
delete root;
return t;
}
root->Right = DelMax(root->Right);
return root;
}
BSTree BSTDel(BSTree root,int x) {
if (root == NULL) return NULL;
if (root->data == x) {
if (! root->Right || !root->Left) {
BSTNode *t = !root->Right ? root->Left : root->Right;
delete root;
return t;
}
root->data = GetMax(root->Left);
root->Left = DelMax(root->Left);
}
else if (x > root->data) root->Right = BSTDel(root->Right, x);
else root->Left = BSTDel(root->Left, x);
return root;
}写法2:
指针很强大,传进 BSTree *root,可以直接修改 *root 的值。(也很烦,上面的写法,如果是JAVA,完全不用考虑delete的问题,代码量可以更短。)
删除含两个子树的节点那部分,可以用 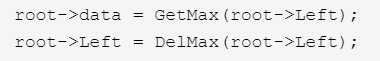 这种思想写,就是不删除,而是用找到的最大结点的值把该结点的值直接替换,再把最大结点删除,效果是一样的,
这种思想写,就是不删除,而是用找到的最大结点的值把该结点的值直接替换,再把最大结点删除,效果是一样的,但我是杠精,偏要复杂写。
void BSTDel(BSTree *root, int x){
if (!*root) {
cout << "找不着" << endl;
return;
}
BSTree p = *root;
if (p->data == x) {
if (!p->Right || !p->Left)
*root = !p->Right ? p->Left : p->Right;
else{
BSTNode *parent = p->Left, *q = p->Left;
if (!q->Right) q->Right = p->Right;
else {
while (q->Right) {
parent = q;
q = q->Right;
}
parent->Right = q->Left;
q->Left = p->Left;
q->Right = p->Right;
}
*root = q;
}
delete p;
}
else if (x > p->data) //向右找
BSTDel(&(p->Right), x);
else if (x < p->data) //向左找
BSTDel(&(p->Left), x);
}引申:二叉排序树的思想和快速排序的partition很像,树的根节点就是快速排序中的第一个切分元素,左侧的值都比它小,右侧的值都比它大,这对于所有的子树同样适用,这和快速排序中对子数组的递归排序也是对应的。
杂:
//下面这是最开始写的,那个时候还不能理解BSTree *root是个什么含义。
//在删除只含单个子树的根节点时会出错。它是错的,但我还是要往上放,666。
void BSTreeDelete(BSTree root, int x) {
if (!BSTreeFind(root, x)) return;
BSTNode *pre = NULL, *p = root;
while (x != p->data) {
pre = p;
p = x < p->data ? p->Left : p->Right;
}
//1. 左右子树都为空
if (p->Left == NULL && p->Right == NULL) {
p->data < pre->data ? pre->Left = NULL : pre->Right = NULL;
delete p;
return;
}
//2. 左子树或右子树为空
if (p->Left == NULL) {
p->data < pre->data ? pre->Left = p->Right : pre->Right = p->Right;
delete p;
}
else if (p->Right == NULL) {
p->data < pre->data ? pre->Left = p->Left : pre->Right = p->Left;
delete p;
}
//3.左右子树都不为空
else {
BSTNode *pre = p->Left, *q = p->Left;
while (q->Right) {
pre = q;
q = q->Right;
}
p->data = q->data;
if (q == p->Left)
p->Left = p->Left->Left;
else //最右边的这个节点只可能有左子树
pre->Right = q->Left;
delete q;
}
}一般二叉排序树是不允许重复数据的,如果实际应用中遇到相同的值,那么向左向右插入都可以,只要保证树在中序遍历时是非严格单调递增即可。但是代码中需要注意一下,否则找爹的时候会找错。。。
BSTree BSTCreat(int *a,int length) {
BSTree T = new BSTNode;
T->data = *a++;
T->Left = NULL;
T->Right = NULL;
for (int i = 1; i < length; i++) {
BSTNode *pre = NULL, *p = T, *Node=new BSTNode;
while (p) {
pre = p;
p = *a < p->data ? p->Left : p->Right;
}
Node->data = *a;
Node->Left = NULL; Node->Right = NULL;
*a < pre->data ? pre->Left = Node : pre->Right = Node;
a++;
}
return T;
}以上是关于数据结构之树篇2——二叉排序(查找,搜索)树的主要内容,如果未能解决你的问题,请参考以下文章