Python描述数据结构之二叉排序树篇

Posted 2021-06-24 夏小悠

文章目录

• • 前言
  • 1. 二叉排序树的定义
  • 2. 二叉排序树的查找
  • 3. 二叉排序树的插入
  • 4. 二叉排序树的构造
  • 5. 二叉排序树的删除
  • 6. 二叉排序树的查找效率分析

前言

  本篇章主要介绍二叉树的应用之一------二叉排序树，包括二叉排序树的定义、查找、插入、构造、删除及查找效率分析。

1. 二叉排序树的定义

  二叉排序树$(Binary$ $Sort$ $Tree,BST)$，也称为二叉查找树，具有以下性质：
  (1) 若左子树非空，则左子树上所有结点的值均小于根结点的值；
  (2) 若右子树非空，则右子树上所有结点的值均大于根结点的值；
  (3) 左、右子树也分别是一棵二叉排序树。
  综上可知，在二叉排序树中：左子树结点的值 < 根结点的值 < 右子树结点的值，所以对二叉排序树进行中序遍历，可以得到一个递增的有序序列。

2. 二叉排序树的查找

  二叉排序树的查找是从根结点开始，沿某个分支逐层向下比较的过程。若二叉排序树非空，先将给定的关键字与根结点的关键字进行比较，若相等，则查找成功；若不相等，如果小于根结点的关键字，则在根结点的左子树上查找，如果大于根结点的关键字，则在根结点的右子树上查找。
  二叉排序树的查找算法：

    def BSTSearch(self, k):
        TreeNode = self.RootNode
        while TreeNode is not None and k != TreeNode.data:
            if k < TreeNode.data:
                TreeNode = TreeNode.lchild
            else:
                TreeNode = TreeNode.rchild
        return TreeNode

3. 二叉排序树的插入

  二叉排序树作为一种动态树表，它的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字等于给定值的结点时插入的。
  插入过程如下：若二叉排序树为空，则直接插入结点；若非空，先将给定的关键字与根结点的关键字进行比较，若小于根结点的关键字，则插入左子树，若大于根结点的关键字，则插入右子树。插入的结点一定是一个新添加的叶结点，且是查找失败时的查找路径上访问的最后一个结点的左孩子或右孩子。
  二叉排序树的插入算法：

    def BSTInsert(self, k):
        TreeNode = self.RootNode
        if TreeNode is None:
            self.RootNode = BiTreeLinkNode(k)
            return True
        while True:
            if k < TreeNode.data:
                if TreeNode.lchild is None:
                    TreeNode.lchild = BiTreeLinkNode(k)
                    return True
                TreeNode = TreeNode.lchild
            elif k > TreeNode.data:
                if TreeNode.rchild is None:
                    TreeNode.rchild = BiTreeLinkNode(k)
                    return True
                TreeNode = TreeNode.rchild
            else:
                return False

4. 二叉排序树的构造

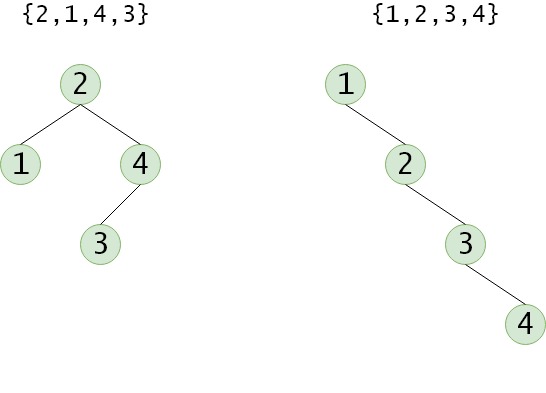
  二叉排序树的构造过程如下：从一棵空树出发，依次输入元素，将它们插入树中的合适位置。关键字的序列不同，构造出来的二叉排序树也会有所不同，比如下图：

  二叉排序树的构造算法：

    def CreateBST(self):
        for val in self.data_list:
            self.BSTInsert(val)
        return self.RootNode

5. 二叉排序树的删除

  在二叉排序树中删除一个结点时，不能把以该结点为根的子树上的结点都删除，必须先把被删除的结点从存储二叉排序树的链表上摘下，将因删除结点而断开的二叉链表重新连接起来，同时确保二叉排序树的性质不会丢失。具体分三种情况：
  (1) 如果被删除的结点是叶结点，可以直接删除；
  (2) 如果被删除的结点只有一棵左子树或右子树，需要让该结点的子树成为该结点的父结点的子树，以替代被删除结点的位置；

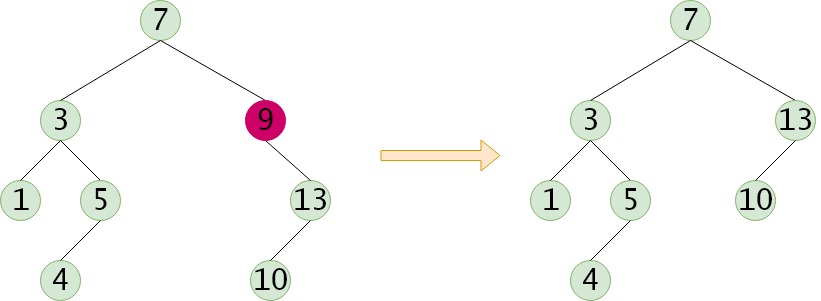
  (3) 被删除的结点有左子树和右子树，需要用该结点的直接后继来代替该结点的位置，然后从二叉排序树中删去这个直接后继。

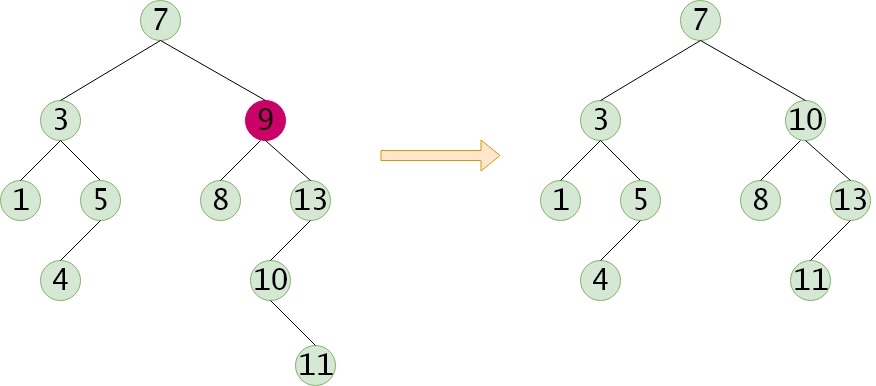
6. 二叉排序树的查找效率分析

  如果二叉排序树的左、右子树的高度之差的绝对值不超过1，则这样的二叉树称为平衡二叉树，它的平均查找长度为$O(lo{g}_{2}n)$；如果二叉排序树是一个只有左子树或右子树的单支树(类似于有序的单链表)，则它的平均查找长度为$O(n)$。
  在等概率情况下，有序列 { 2 , 1 , 4 , 3 } \\{2,1,4,3\\} {2,1,4,3}构成的排序二叉树的查找成功的平均查找长度为
$$ASL=\frac{1+2\times 2+3}{4}=2$$  有序列 { 1 , 2 , 3 , 4 } \\{1,2,3,4\\} {1,2,3,4}构成的排序二叉树的查找成功的平均查找长度为
$$ASL=\frac{1+2+3+4}{4}=2.5$$  二叉排序树的查找效率主要取决于树的高度，如果要提高查找效率，在构造二叉排序时最好不要使用有序的序列，尽量构造平衡二叉树。

  有关平均查找长度$ASL$的知识会在查找这部分再说。