笛卡尔树学习笔记

Posted 2023-01-25 wwwaax

笛卡尔树

下文的资料多摘自OI Wiki

性质

笛卡尔树是一种二叉树，每一个节点都由一个键值二元组 \\((k,w)\\) 构成。要求 \\(k\\) 满足二叉搜索树的性质，而 \\(w\\) 满足堆的性质。如果笛卡尔树的 \\(k\\) ，\\(w\\) 键值确定的话，且 \\(k\\) 互不相同，\\(w\\) 互不相同，那么这个笛卡尔树的结构是唯一的。

例如 OI Wiki 上的这张图：

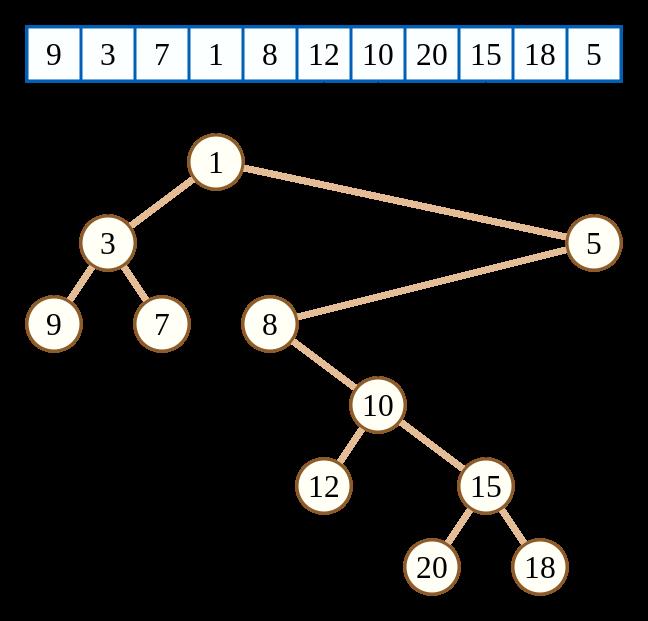
上面的这棵树是按每一个点内的值为键值 \\(w\\)，把数组下标当作键值 \\(k\\)，来建立的。仔细观察可以发现，这棵树的 \\(k\\) 满足二叉搜索树的性质，而键值 \\(w\\) 是满足小根堆的性质的。

像上面这棵树一样键值 \\(k\\) 恰好对应数组下标的笛卡尔树有一个性质：一棵子树内的下标是连续的一个区间（满足二叉搜索树的性质）。

谈到笛卡尔树，很容易让人想到一种家喻户晓的结构—— Treap。没错，Treap 是笛卡尔树的一种，只不过 \\(w\\) 的值完全随机。Treap 也有线性的构建算法，如果提前将元素排好序，显然可以使用上述单调栈算法完成构建过程，只不过很少会这么用。

构建

过程

我们考虑将元素的键值 \\(k\\) 进行排序，然后一个一个地插入到当前的笛卡尔树中，那么我们每一次插入的元素必在这个树的右链（右链：从根节点一直往右子树走，经过的节点）的末端。于是我们可以执行这样一个过程，从下往上比较右链节点与当前节点的 \\(u\\)，和\\(w\\)，如果找到了一个右链上的节点满足 \\(x_w<u_w\\)，就把 \\(u\\) 接到 \\(x\\) 的有儿子上，而 \\(x\\) 原来的右子树就变成了 \\(u\\) 的左子树。

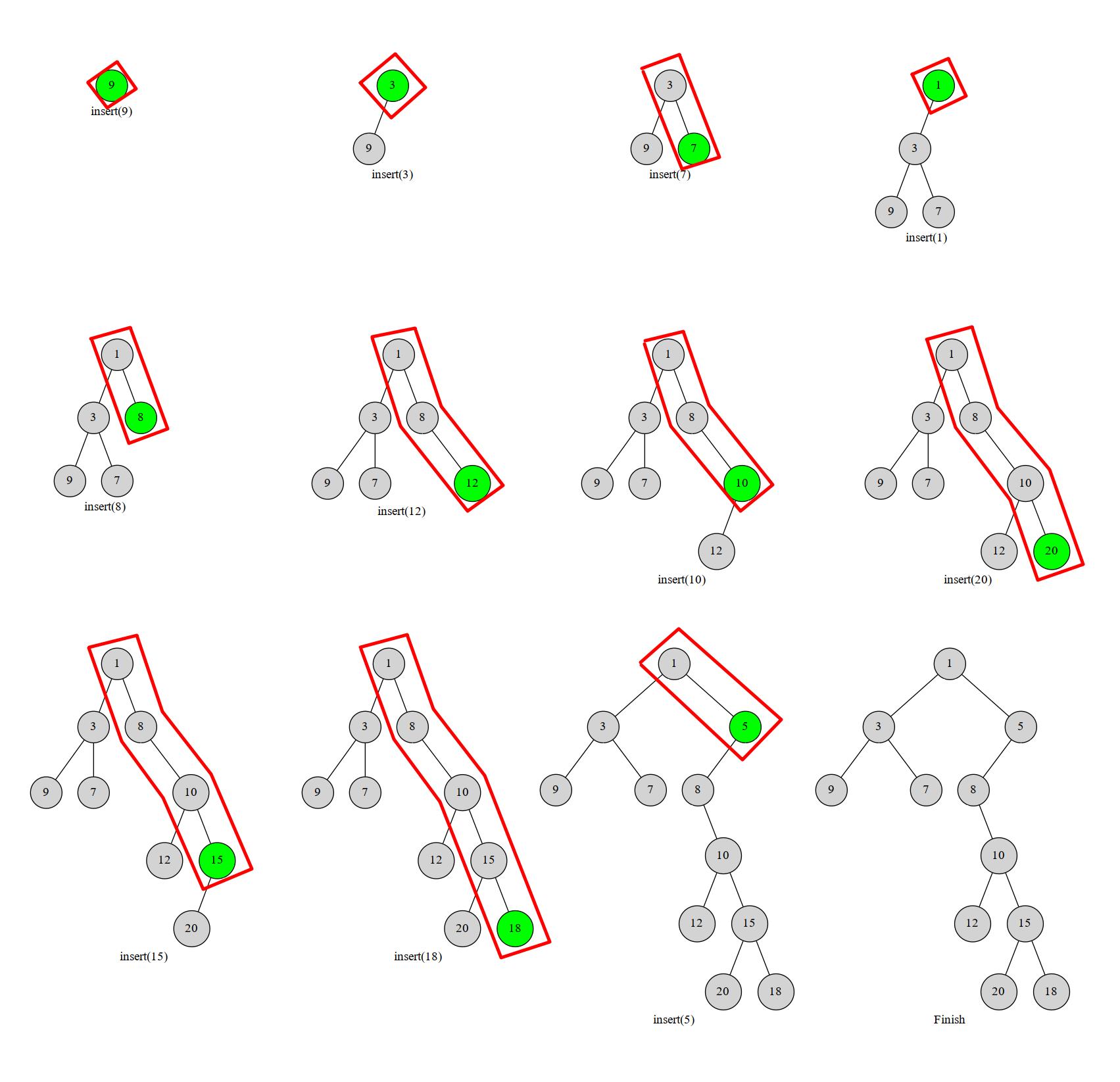
显然每个数最多进出右链一次（或者说每个点在右链中存在的是一段连续的时间）。这个过程我们可以用栈维护，栈中维护当前笛卡尔树的右链上的结点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次，复杂度 \\(O(n)\\)。

实现

for (int i = 1; i <= n; i++) 
  int k = top;
  while (k > 0 && h[stk[k]] > h[i]) k--;
  if (k) rs[stk[k]] = i;  // rs代表笛卡尔树每个节点的右儿子
  if (k < top) ls[i] = stk[k + 1];  // ls代表笛卡尔树每个节点的左儿子
  stk[++k] = i;
  top = k;