学习数据结构笔记(21) --- [克鲁斯卡尔算法(Kruskal Algorithm) 由公交车站连接问题引入]

Posted 2022-01-07 小智RE0

B站学习传送门–>尚硅谷Java数据结构与java算法（Java数据结构与算法）

---

文章目录

• • 情景引入
  • 分析
  • 解决

情景引入

某个城市需要连接7个公交站;需要设计出最短路径的路线进行建设;

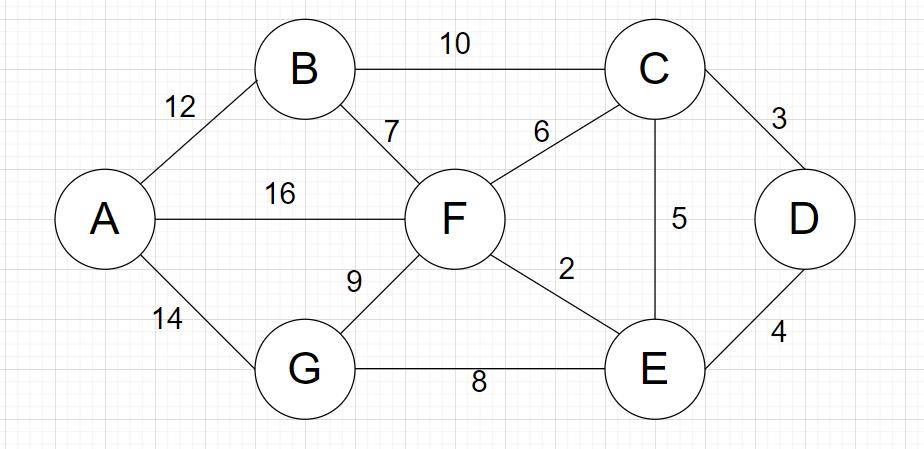
克鲁斯卡尔算法
与普里姆算法不同，它的时间复杂度为O（eloge）（e为网中的边数）;
适合于求边稀疏的网的最小生成树

分析

先找到权值最小的边FE;进行连接

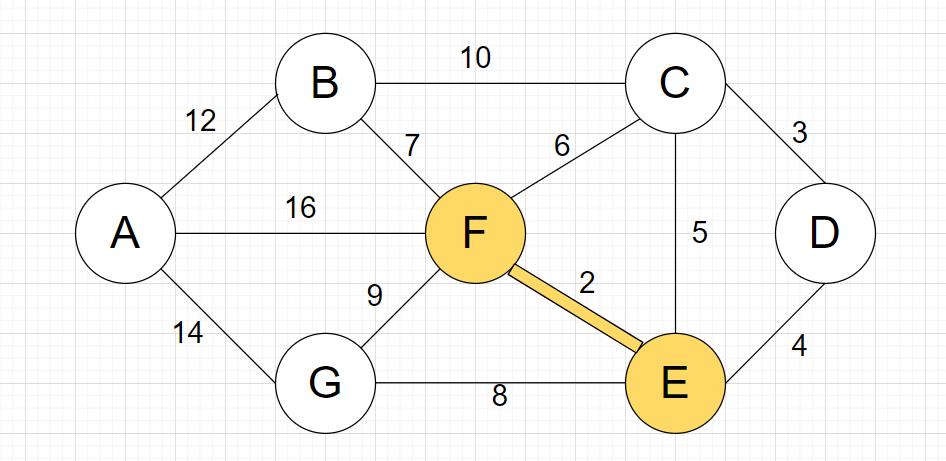
排除已使用的边,找到权值最小的边CD;连接

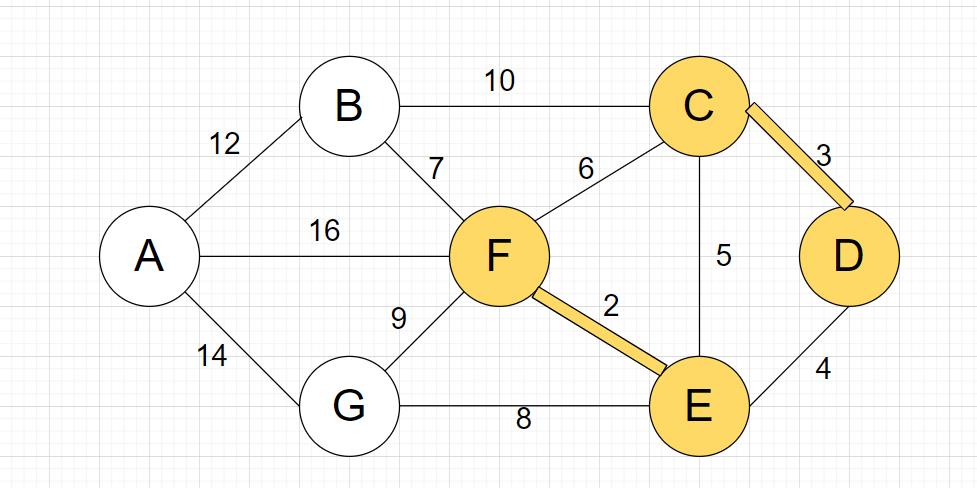
找到权值最小的边DE;连接

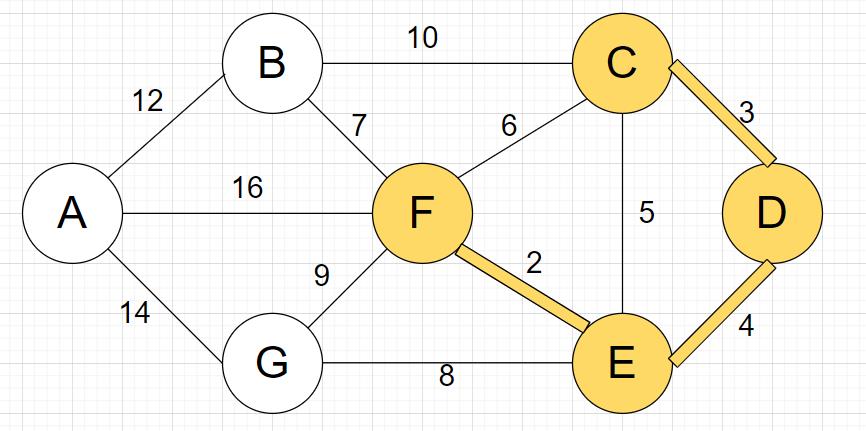
在不构成回路的情况下,找到权值小的边BF;连接

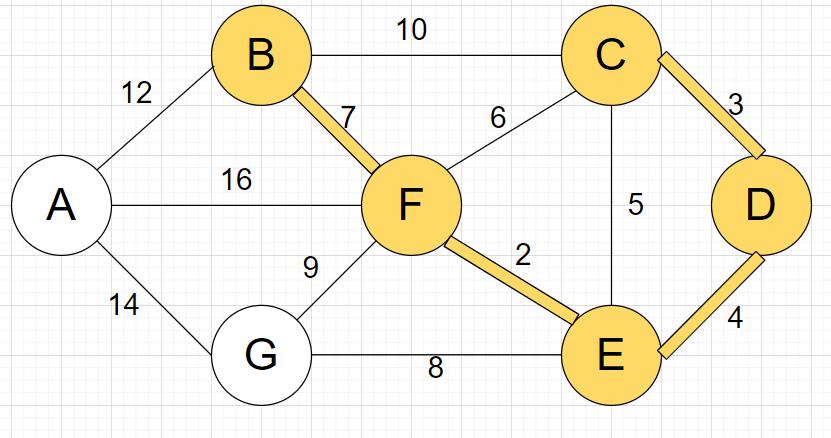
不构成回路的情况下,找到权值小的边GE;

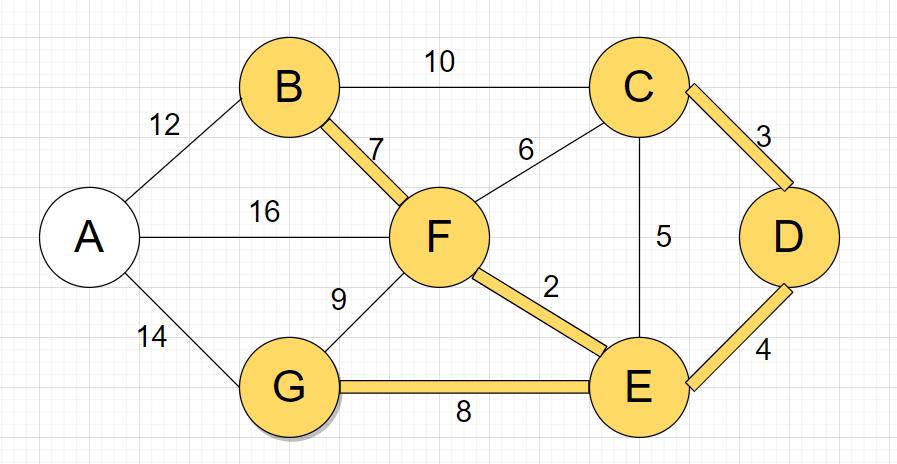
在不构成回路的情况下,找到权值小的边AB

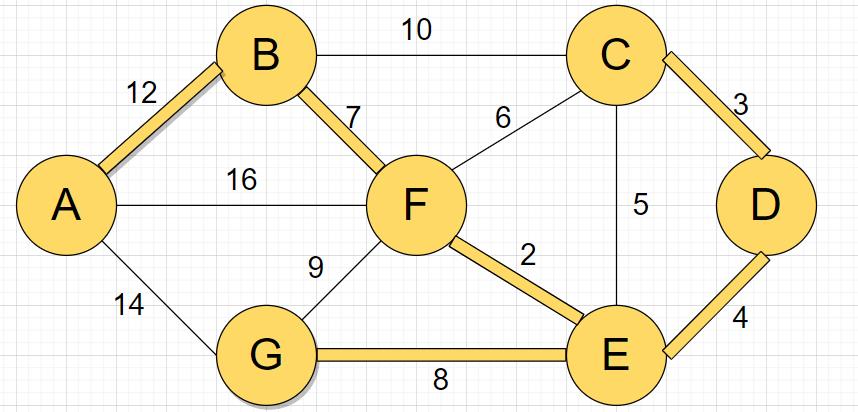
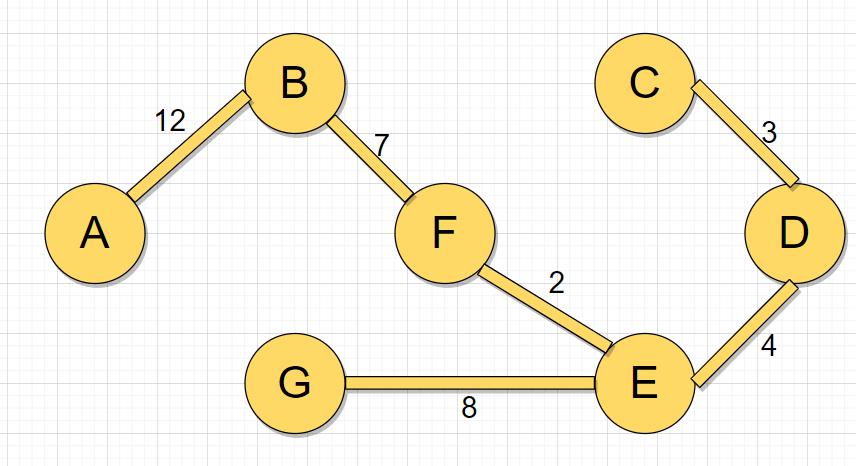
解决

具体的实现解决过程

package day22kruskalalgorithm;
/**
 * @author by CSDN@小智RE0
 * @date 2021-12-07
 * 克鲁斯卡尔算法
 */
public class KruskalAlgorithm 
    //测试使用;
    public static void main(String[] args) 
        char[] busStop = 'A', 'B', 'C', 'D', 'E', 'F', 'G';
        //邻接矩阵描绘;
        int[][] adjacencyMatrix = 
                0, 12, BAN, BAN, BAN, 16, 14,
                12, 0, 10, BAN, BAN, 7, BAN,
                BAN, 10, 0, 3, 5, 6, BAN,
                BAN, BAN, 3, 0, 4, BAN, BAN,
                BAN, BAN, 5, 4, 0, 2, 8,
                16, 7, 6, BAN, 2, 0, 9,
                14, BAN, BAN, BAN, 8, 9, 0
        ;
        //初始化类;
        KruskalAlgorithm ka = new KruskalAlgorithm(busStop, adjacencyMatrix);
        //初始化打印;
        ka.toStrings();
        //进行排序;
        ka.getSide();
        //System.out.println(Arrays.deepToString(kaSide));
        //最终路径;
        ka.finallyMethod();
    

    //边的个数;
    private int sideNum;
    //图中顶点的;
    private final char[] peak;
    //邻接矩阵存储顶点之间的边连接关系;
    private final int[][] adjacencyMatrix;
    //禁止连通的边的标志;
    private static final int BAN = Integer.MAX_VALUE;

    //初始化构造;
    public KruskalAlgorithm(char[] peak, int[][] adjacencyMatrix) 
        this.peak = new char[peak.length];
        //将顶点初始化;
        System.arraycopy(peak, 0, this.peak, 0, peak.length);

        this.adjacencyMatrix = new int[peak.length][peak.length];
        //二维数组初始化;
        System.arraycopy(adjacencyMatrix, 0, this.adjacencyMatrix, 0, adjacencyMatrix.length);
        //边的数量数组初始化;
        for (int i = 0; i < this.adjacencyMatrix.length; i++) 
            for (int j = i + 1; j < this.adjacencyMatrix.length; j++) 
                if (this.adjacencyMatrix[i][j] != BAN) 
                    sideNum++;
                
            
        
    

    //根据输入的顶点字符寻找该字符的索引;输入错误则返回-1;
    public int findIndexByPeak(char p) 
        for (int i = 0; i < this.peak.length; i++) 
            if (peak[i] == p) 
                return i;
            
        
        return -1;
    

    //获取图里的边; 实际就是从邻接矩阵中进行过滤;
    public Side[] getSide() 
        int k = 0;
        Side[] res = new Side[this.sideNum];
        for (int i = 0; i < this.adjacencyMatrix.length; i++) 
            for (int j = i + 1; j < this.adjacencyMatrix.length; j++) 
                if (this.adjacencyMatrix[i][j] != BAN) 
                    res[k++] = new Side(this.peak[i], this.peak[j], this.adjacencyMatrix[i][j]);
                
            
        
        return res;
    

    //获取指定索引的顶点的这条边的结束点;
    public int getEndIndex(int[] endCollect, int index) 
        //终点集合数组:在连接时逐渐形成;
        while (endCollect[index] != 0) 
            index = endCollect[index];
        
        return index;
    

    //对于图的边进行冒泡排序;
    private void sortEng(Side[] sides) 
        for (int i = 0; i < sides.length - 1; i++) 
            for (int j = 0; j < sides.length - i - 1; j++) 
                if (sides[j].weight > sides[j + 1].weight) 
                    //用临时数作为中介;
                    Side temp = sides[j];
                    sides[j] = sides[j + 1];
                    sides[j + 1] = temp;
                
            
        
    

    //输出邻接矩阵关系;
    public void toStrings() 
        System.out.println("--该图的邻接矩阵--");
        for (int[] matrix : this.adjacencyMatrix) 
            for (int j = 0; j < this.adjacencyMatrix.length; j++) 
                System.out.printf("%15d", matrix[j]);
            
            System.out.println();
        
        System.out.println("---------------");
    

    //最终方法;---------------------------------
    public void finallyMethod() 
        //结果集数组的索引;
        int resIndex = 0;
        //最终的最小生成树的顶点连接的边的终点数组;
        int[] endCollect = new int[sideNum];
        //结果数组;
        Side[] resArr = new Side[sideNum];
        //图中所有边的集合;
        Side[] sideArr = getSide();
        //当前这个图,边的集合输出打印;
        //Arrays.stream(sideArr).forEach(a -> System.out.print(a + " "));
        //System.out.println("共有" + sideArr.length + "条边");
        //按照边的权值大小;排序操作;
        sortEng(sideArr);
        //遍历数组;添加时判断是否构成回路;
        for (Side side : sideArr) 
            //当前边的起点;
            int s1 = findIndexByPeak(side.startPeak);
            //当前边的终点;
            int s2 = findIndexByPeak(side.endPeak);
            //判断是否已经有回路了;
            int end1 = getEndIndex(endCollect, s1);
            int end2 = getEndIndex(endCollect, s2);
            //没有回路;
            if (end1 != end2) 
                endCollect[end1] = end2;
                resArr[resIndex++] = side;
            
        
        System.out.println("---------结果集---------");
        // Arrays.stream(resArr).forEach(System.out::println);
        for (int i = 0; i < resIndex; i++) 
            System.out.println(resArr[i]);
        
    



//该类来表示连接的边;
class Side 
    char startPeak;
    char endPeak;
    //边的权值;
    int weight;

    //初始化边类;
    public Side(char startPeak, char endPeak, int weight) 
        this.startPeak = startPeak;
        this.endPeak = endPeak;
        this.weight = weight;
    

    //打印边;
    @Override
    public String toString() 
        return "Side" +
                "startPeak=" + startPeak +
                ", endPeak=" + endPeak +
                ", weight=" + weight +
                '';
    

测试结果

--该图的邻接矩阵--
              0             12     2147483647     2147483647     2147483647             16             14
             12              0             10     2147483647     2147483647              7     2147483647
     2147483647             10              0              3              5              6     2147483647
     2147483647     2147483647              3              0              4     2147483647     2147483647
     2147483647     2147483647              5              4              0              2              8
             16              7              6     2147483647              2              0              9
             14     2147483647     2147483647     2147483647              8              9              0
---------------
---------结果集---------
SidestartPeak=E, endPeak=F, weight=2
SidestartPeak=C, endPeak=D, weight=3
SidestartPeak=D, endPeak=E, weight=4
SidestartPeak=B, endPeak=F, weight=7
SidestartPeak=E, endPeak=G, weight=8
SidestartPeak=A, endPeak=B, weight=12