数据结构学习笔记——图的应用1(最小生成树最短路径)
Posted 晚风(●•σ )
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构学习笔记——图的应用1(最小生成树最短路径)相关的知识,希望对你有一定的参考价值。
目录
一、最小生成树
- 一个含有n个顶点的连通图G,若它的一棵带权生成树的各边权值之和最小,则称该生成树为图G的
最小生成树,该树包含图的所有顶点,其边的个数为n-1;在生成最小生成树时可以选择不同的边,所以最小生成树不唯一;但若当图G的各边权值不同,则此时最小生成树是唯一的。
产生图的最小生成树主要有两个算法,分别是普里姆算法(Prim)和克鲁斯卡尔算法(Kruskal)。
二、普里姆算法(Prim)
普里姆算法步骤
- 图G=(V,E)是一个含有n个顶点的连通图,普里姆算法的步骤如下:
1、从顶点集V中任意选取一个顶点,然后将与该顶点邻接的边中选取一条权值最小的边,将其并入,从而得到一棵树;
2、继续选取邻接的边中最短的边(权值最小),并入树中;
3、直到图中的所有顶点都被并入,得到最小生成树。
例如,下面是一个无向带权连通图,采用普里姆算法生成最小生成树:
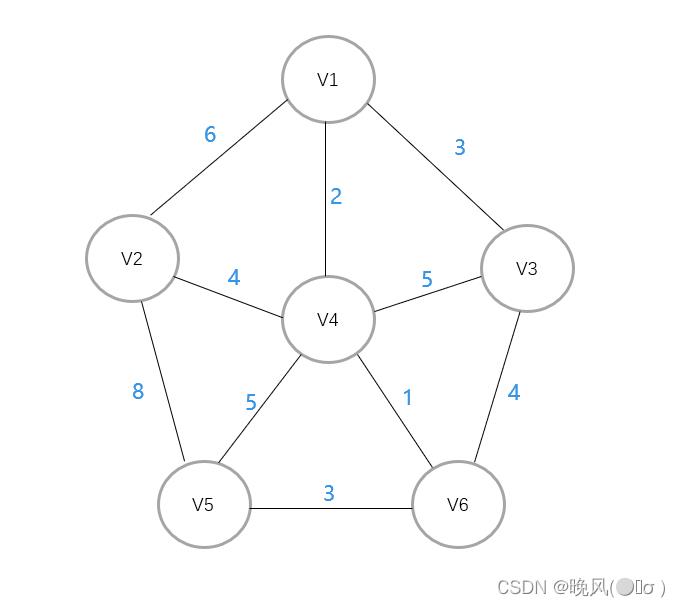
1、任意选取一个顶点为起点开始,这里选取V1为例。
2、此时邻接的边的权值分别为2、3、6,取最小权值2,V1与邻接的顶点V4相连:
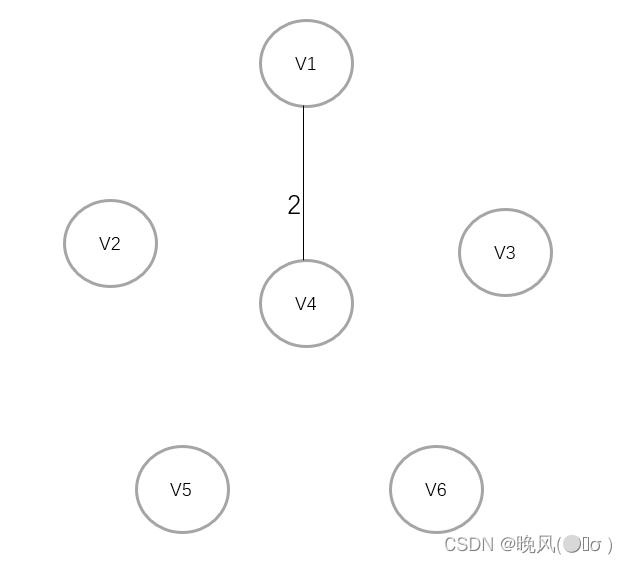
3、此时邻接的边的权值分别为1、4、5、5,以及加上前面的3、6,取最小权值1,V4与邻接的顶点V6相连:

4、此时邻接的边的权值分别为3、4,以及加上前面的3、6、4、5、5,取最小权值3,取的是与该顶点和对应边距离最近的顶点,V6与邻接的顶点V5相连:
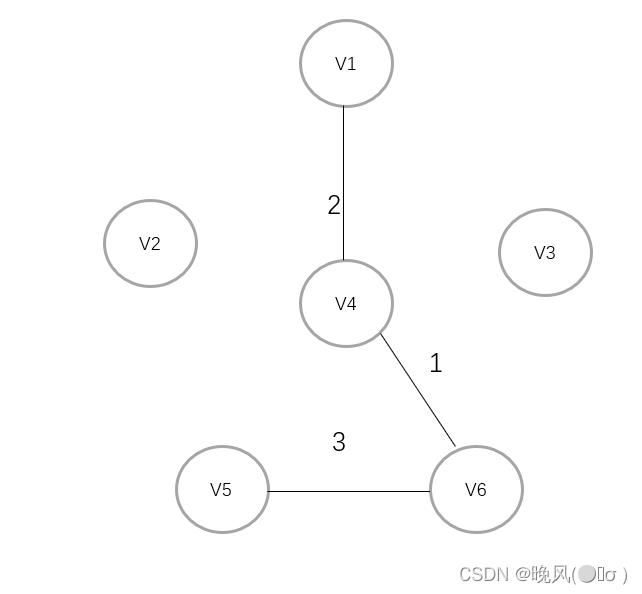
5、取此时最小权值,取的是当前图中剩余各边对应权值中最小的权值,即3,V1与V3相连:
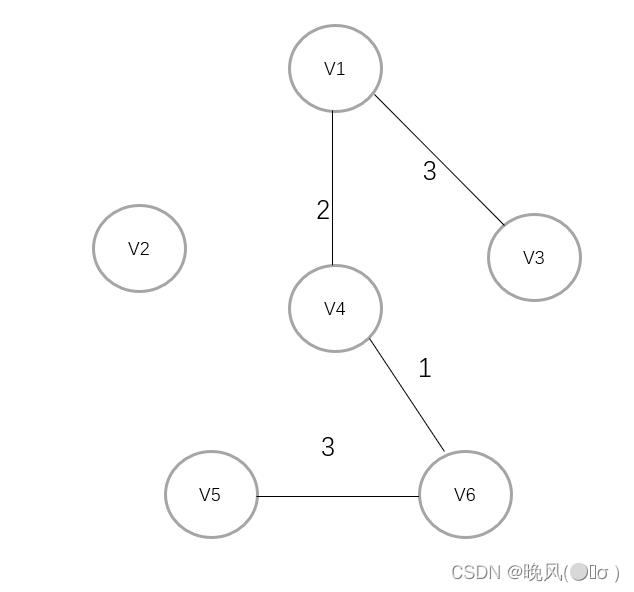
6、取此时最小权值,即4,V4与V2相连,至此所有顶点都被访问到,得到最小生成树:
- ✨图G=(V,E),在邻接矩阵的存储结构下,普里姆算法的时间复杂度为O(|V|2),它适用于求解
稠密图的最小生成树。
三、克鲁斯卡尔算法(Kruskal)
- 克鲁斯卡尔算法中将图的所有边对应的权值
按照从小到大的顺序依次开始选取,若选取的某边与先前的树构成回路,则舍去,一直进行下去,直到所有顶点被访问到,当生成树的边的个数为n-1时为止,即可得到最小生成树。
(一)并查集
这里的判断是否构成回路,要使用到并查集,并查集中的树可以通过一个结点找到其双亲结点,从而找到根结点,即用到了树的双亲存储结构:
双亲表示法是通过采用一维数组来存储树中的结点,其中每个结点被赋予一个结构体类型,包含data域和parent域,分别存储结点的数据域和存储该结点双亲的数组下标,通过双亲表示法中可以很容易地找到每个结点的双亲和祖先。
通过这种表示法可以很快地找到两个含有多个元素的集合将其并为一个,两个集合相当于并查集中的两棵树,只需找到一棵树的根结点,然后将其作为另一颗树的某一结点的孩子结点,如下:

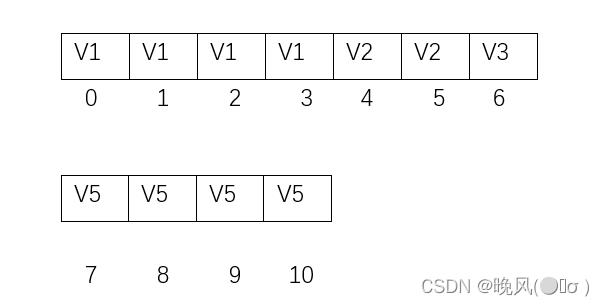
例如,将第二棵树的根结点作为第一颗树V4结点的孩子结点,即可得到:
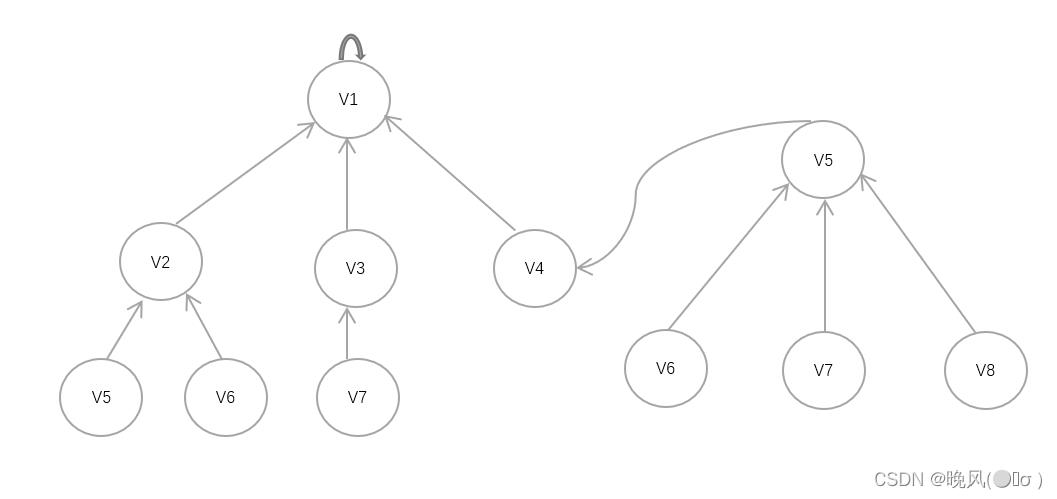

从而可以在判断是否形成回路时,判断两个顶点是否属于同一棵树中的集合,即找到它们的根结点,若有相同的根结点,则说明是同一个集合,以此来完成克鲁斯卡尔算法。
(二)克鲁斯卡尔算法步骤
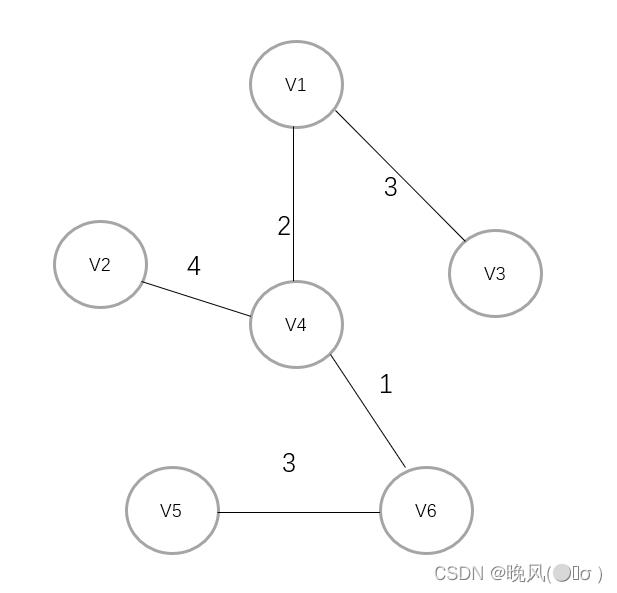
例如,下面是一个无向带权连通图,采用普里姆算法生成最小生成树:
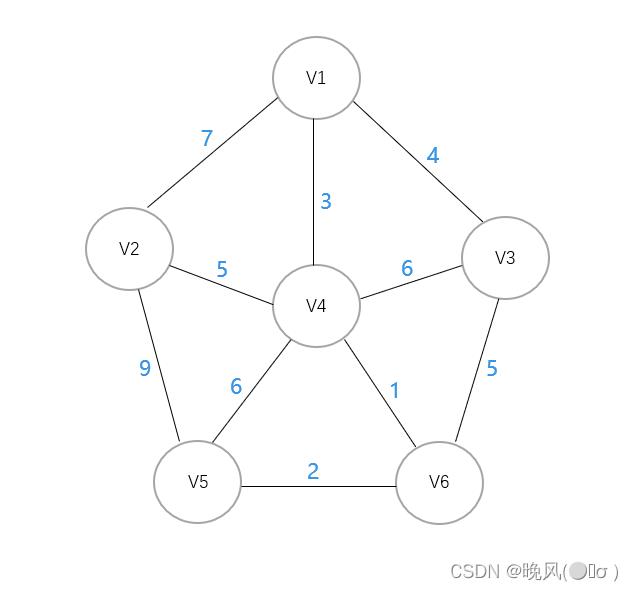
1、将图中所有边对应的权值,按从小到大排序如下:1,2,3,4,5,6,8。
2、可知权值1最小,首先连接V4和V6:
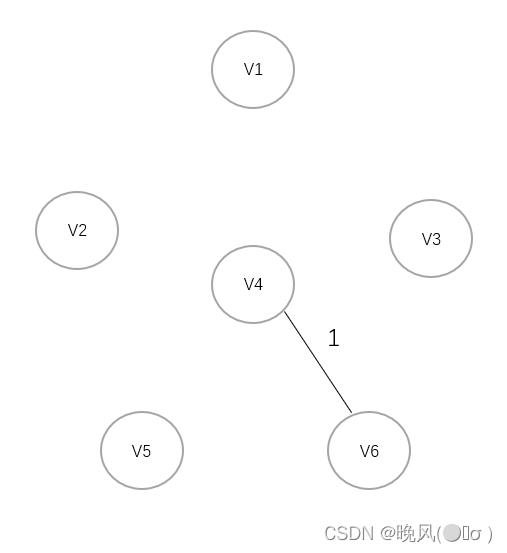
3、选择权值2,连接V6与V5:

3、选择权值3,选取V4与V1连接:
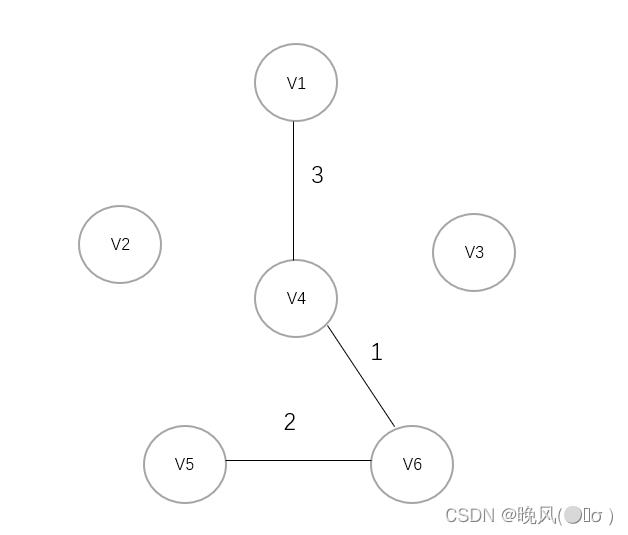
4、选择权值4,连接V1与V3:
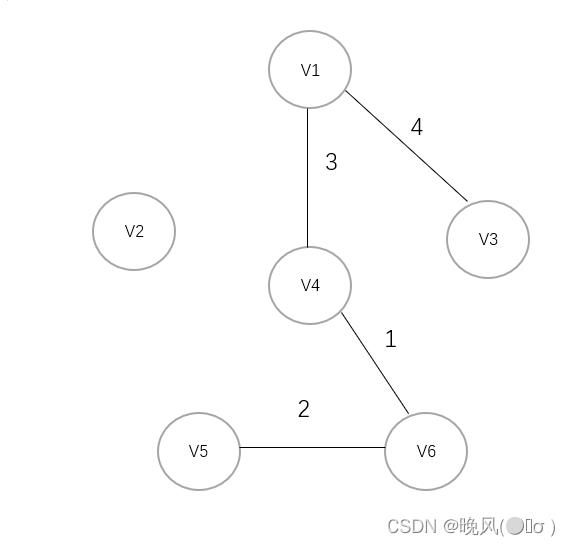
5、选取权值5,连接V4与V2,最终得到最小生成树如下:
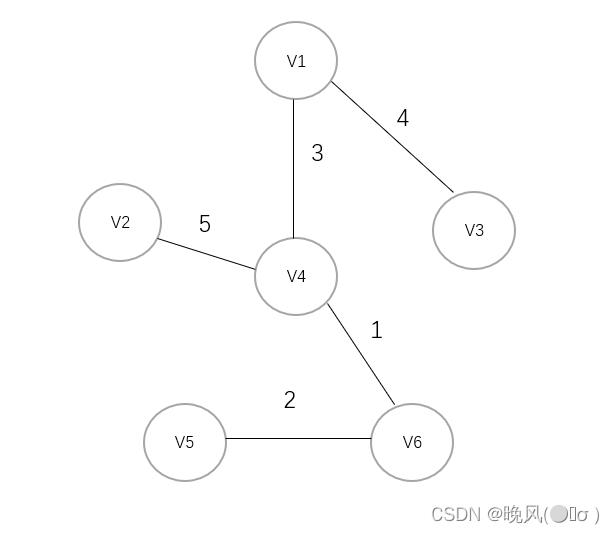
- ✨图G=(V,E),克鲁斯卡尔算法中由于要对所有的边的权值按从小到大进行排序,所以其时间复杂度取决于排序算法,其规模由图的边数E决定,相较于普里姆算法,它适用于求
稀疏图或顶点较多的图的最小生成树。
四、最短路径
(一)最短路径的概念
在树中,一个结点和另一个结点之间的分支即为这两个结点之间的路径。
- 在带权图中,一个顶点到另一个顶点所经过边的权值之和称为该路径的带权路径长度,由于可能路径不止一条,所以将带权路径长度最短的那条路径称为
最短路径,最短路径的求解问题可分为两类:求单源最短路径和求一对顶点之间最短路径,分别由迪杰斯特拉算法和弗洛伊德算法求解。
(二)迪杰斯特拉算法
求带权有向图中一个顶点到其他顶点的最短路径,采用迪杰斯特拉算法,用于求单源最短路径。
- 以图中某一顶点为起始点开始,寻找到终点的路径,每次遍历寻找的是距离最近(带权值最小)且未被访问的邻接顶点,遍历到终点为止,最后得到的是一条带权路径长度之和最小的路径。
例如,下面是一个带权有向图,通过迪杰斯特拉算法求其最短路径(若以图中V1顶点为起始点,求到其余顶点V2、V3、V4、V5、V6的最短路径):
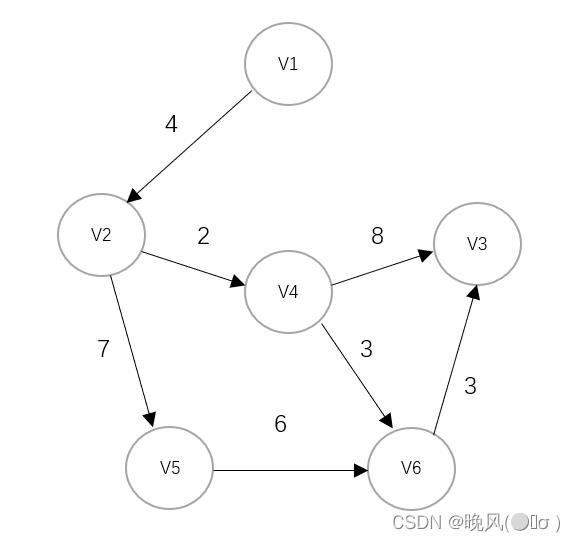
V1→V2:只有一条路径,即V1→V2,路径长度为4;
V1→V3:有三条路径,分别是V1→V2→V4→V3,路径长度为4+2+8=14、V1→V2→V4→V6→V3,路径长度为4+2+3+3=12、V1→V2→V5→V6→V3,路径长度为4+7+6+3=20,故最短路径为V1→V2→V4→V6→V3,即12;
V1→V4:只有一条路径,即V1→V2→V4,路径长度为4+2=6;
V1→V5:只有一条路径,即V1→V2→V5,路径长度为4+7=11;
V1→V6:有两条路径,分别是V1→V2→V4→V6,路径长度为4+2+3=9、V1→V2→V5→V6,路径长度为4+7+6=17,最短路径为V1→V2→V4→V6,即9。
如下表(以V1为起始点为例):
| 起始点 | 终点 | 最短路径 | 路径长度 |
|---|---|---|---|
| V1 | V2 | V1→V2 | 4 |
| V3 | V1→V2→V4→V6→V3 | 12 | |
| V4 | V1→V2→V4 | 6 | |
| V5 | V1→V2→V5 | 11 | |
| V6 | V1→V2→V4→V6 | 9 |
- ✨对于图G=(V,E),在邻接矩阵的存储结构下,迪杰斯特拉算法时间复杂度为O(|V|2)。
(三)弗洛伊德算法
1、弗洛伊德算法步骤
弗洛伊德算法用于求一对顶点之间的最短路径,其步骤如下:
- 若对于图中的顶点vi和顶点vj,规定若两个顶点之间存在边,则将该边上的权值作为其最短路径长度,否则以∞表示其最短路径长度;
- 然后在每条路径中加入中间顶点,若加入后的路径长度减少了,则新路径替换旧路径,得到新的最短路径长度。
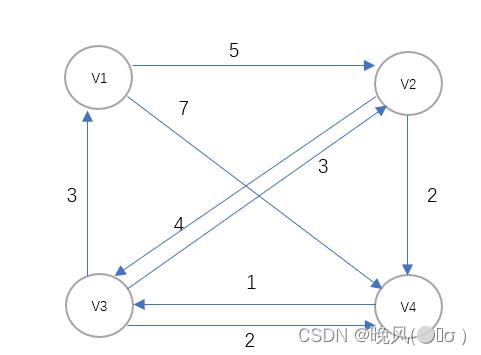
例如,对于下面这个带权有向图G,其邻接矩阵如下,对其进行弗洛伊德算法求每一对顶点之间的路径:

以一个顶点为中间点(以0为例),对图中的所有顶点对vi,vj,即V1,V2,V1,V3,V1,V2,V2,V1,V2,V3,V2,V4,V3,V1,V3,V2,V3,V4,V4,V1,V4,V2,V4,V3,设当前访问的顶点对为vi,vj,若A[vi][vj]>A[i][0]+A[0][j],则用A[i][0]+A[0][j]替换A[vi][vj]。
1、初始A-1为原邻接矩阵。以V1为中间点,未发现要替换的顶点,更新后的方阵标记为A0,所以A-1和A0都为如下:
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | 0 | 5 | ∞ | 7 |
| V2 | ∞ | 0 | 4 | 2 |
| V3 | 3 | 3 | 0 | 2 |
| V4 | ∞ | ∞ | 1 | 0 |
我们另设一个矩阵Path,将开始时所有矩阵元素都置为1,所以在以V1为中间点后,得到的Path-1和Path0如下:
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | -1 | -1 | -1 | -1 |
| V2 | -1 | -1 | -1 | -1 |
| V3 | -1 | -1 | -1 | -1 |
| V4 | -1 | -1 | -1 | -1 |
2、以V2为中间点,也是检查所有的顶点对,若A[vi][vj]>A[i][1]+A[1][j],则用A[i][1]+A[1][j]替换A[vi][vj]。其中由于A[0][2]>A[0][1]+A[1][2]=5+4=9,所以将矩阵中的第一行第三列,即A[0][2]替换为A[0][1]+A[1][2],∞替换为9,如下得到A1:
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | 0 | 5 | 9 | 7 |
| V2 | ∞ | 0 | 4 | 2 |
| V3 | 3 | 3 | 0 | 2 |
| V4 | ∞ | ∞ | 1 | 0 |
以V2为中间点,更改后的Path1如下(由于是在矩阵中,按从0开始,V2为中间点此时算1,也就是将-1替换为1):
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | -1 | -1 | 1 | -1 |
| V2 | -1 | -1 | -1 | -1 |
| V3 | -1 | -1 | -1 | -1 |
| V4 | -1 | -1 | -1 | -1 |
3、以V3为中间点,检查所有的顶点对,若A[vi][vj]>A[i][2]+A[2][j],则用A[i][2]+A[2][j]替换A[vi][vj]。其中由于A[1][0]>A[1][2]+A[2][0]=4+3=7,A[3][1]>A[3][2]+A[2][1]=1+3=4,A[3][0]>A[3][2]+A[2][0]=1+3=4,所以将以上都替换为相应的值,如下得到A2:
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | 0 | 5 | 9 | 7 |
| V2 | 7 | 0 | 4 | 2 |
| V3 | 3 | 3 | 0 | 2 |
| V4 | 4 | 4 | 1 | 0 |
以V3为中间点,更改后的Path2如下(由于是在矩阵中,按从0开始,V3为中间点此时算2,也就是将相应的值替换为2):
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | -1 | -1 | 1 | -1 |
| V2 | 2 | -1 | -1 | -1 |
| V3 | -1 | -1 | -1 | -1 |
| V4 | 2 | 2 | -1 | -1 |
4、以V4为中间点,检查所有的顶点对,若A[vi][vj]>A[i][3]+A[3][j],则用A[i][3]+A[3][j]替换A[vi][vj]。其中由于A[0][2]>A[0][3]+A[3][2]=7+1=8,A[1][0]>A[1][3]+A[3][0]=2+4=6,A[1][2]>A[1][3]+A[3][2]=2+1=3,所以将以上都替换为相应的值,如下得到A3:
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | 0 | 5 | 8 | 7 |
| V2 | 6 | 0 | 3 | 2 |
| V3 | 3 | 3 | 0 | 2 |
| V4 | 4 | 4 | 1 | 0 |
以V3为中间点,更改后的Path3如下(由于是在矩阵中,按从0开始,V4为中间点此时算3,也就是将相应的值替换为3):
| V1 | V2 | V3 | V4 | |
|---|---|---|---|---|
| V1 | -1 | -1 | 3 | -1 |
| V2 | 3 | -1 | 3 | -1 |
| V3 | -1 | -1 | -1 | -1 |
| V4 | 2 | 2 | -1 | -1 |
访问所以顶点完成,得到的两个矩阵A和Path如下:

2、求最短路径
- 通过弗洛伊德算法得到的两个矩阵,其中从矩阵A中可以直接得到图中
任意两个顶点的最短路径。
例如,顶点V1到顶点V4的最短路径即为A[0][3]=7,顶点V2到顶点V4的最短路径即为A[1][3]=2(注:矩阵从0下标开始)。
- 由矩阵A和矩阵Path可以得到图在
任意两个顶点之间最短路径上的顶点序列或边序列。
例如,要求顶点V2到顶点V1之间的最短路径顶点序列:
1、通过矩阵A可知,A[1][0]=6,所以顶点V2到顶点V1之间的最短路径为6;
2、由矩阵Path可知,Path[1][0]=3,所以顶点V2到顶点V1之间要经过顶点V4;
3、以V4作为起点,求顶点V4到顶点V1之间,由矩阵Path可知,Path[3][0]=2,所以顶点V4到顶点V1之间要经过顶点V3;
4、以V3作为起点,求顶点V3到顶点V1之间,由矩阵Path可知,Path[2][0]=-1,所以顶点V3到顶点V1之间有直接的边,到此结束;
5、得到顶点V2到顶点V1之间的最短路径顶点序列为:V2→V4→V3→V1。
- ✨对于图G=(V,E),由于其算法代码中有三个for循环嵌套,从而完成以某顶点为中间点时对所有的顶点对进行检查和替换操作,故弗洛伊德算法时间复杂度为O(|V|3)。
以上是关于数据结构学习笔记——图的应用1(最小生成树最短路径)的主要内容,如果未能解决你的问题,请参考以下文章