二叉树基础

Posted 2022-02-10 黑质白章

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二叉树基础相关的知识，希望对你有一定的参考价值。

一、二叉树定义

二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。

总结：每个人最多有2个孩子，但每个孩子只能有一个爸爸。

二、二叉树的前序、中序、后序遍历

给定一个二叉树集合，如何换为二叉树？

例：List = [8,9,96,34,19,69,72,null,null,24,57,25,47,68,null]

public class BinaryTreeTest

public static void main(String[] args)

Integer targetSum = 22;

List<Integer> binaryTreeList = Arrays.asList(8,9,96,34,19,69,72,null,null,24,57,25,47,68,null);

List<TreeNode> nodes = new ArrayList<>();

for (Integer integer : binaryTreeList)

nodes.add(new TreeNode(integer == null ? 0:integer));

//构建二叉树

if (nodes.size() > 0)

for (int i = 0; i < binaryTreeList.size()/2 ; i++)

//左

if (nodes.get(2*i + 1) != null)

nodes.get(i).left = nodes.get(2*i + 1);

//右

if (binaryTreeList.get(2*i + 2) != null)

nodes.get(i).right = nodes.get(2*i + 2);

printBinaryTreeOfPreOrder(nodes.get(0));

System.out.println();

System.out.println("result:"+pathSum(nodes.get(0), targetSum));

//前序

private static void printBinaryTreeOfPreOrder(TreeNode node)

if (node != null)

System.out.print(node.getVal()+",");

printBinaryTreeOfPreOrder(node.getLeft());

printBinaryTreeOfPreOrder(node.getRight());

@Getter

@Setter

class TreeNode

Integer val;

TreeNode left;

TreeNode right;

TreeNode()

TreeNode(Integer val)

this.val = val;

TreeNode(int val, TreeNode left, TreeNode right)

this.val = val;

this.left = left;

this.right = right;

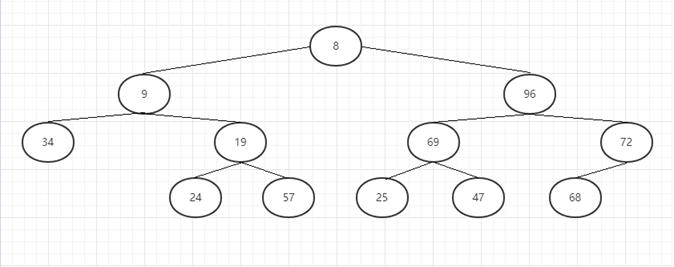
1、前序遍历根节点-左子-右子 (代码见上)

输出：8,9,34,19,24,57,96,69,25,47,72,68

2、中序遍历左子-根节点-右子

输出：34,9,24,19,57,8,25,69,47,96,68,72

//中序

private static void printBinaryTreeOfInfix(TreeNode node)

if (node != null)

printBinaryTreeOfInfix(node.getLeft());

System.out.print(node.val+",");

printBinaryTreeOfInfix(node.getRight());

3、后续遍历左子-右子-根节点

输出：34,24,57,19,9,25,47,69,68,72,96,8

//后序

private static void printBinaryTreeOfPostOrder(TreeNode node)

if (node != null)

printBinaryTreeOfPostOrder(node.getLeft());

printBinaryTreeOfPostOrder(node.getRight());

System.out.print(node.val+",");

以上是关于二叉树基础的主要内容，如果未能解决你的问题，请参考以下文章