短线买股赚钱的概率有多大？python带你来分析

Posted 7758520lzy

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了短线买股赚钱的概率有多大？python带你来分析相关的知识，希望对你有一定的参考价值。

股票操作讲究低买高卖，如果你能买在低点，卖在高点，那么你就是高手；如果你能买在高点，卖在低点，那么你就是“韭菜”。所谓“一盈两平七亏”，对应的是中国的 A 股市场中有 10% 的高手和 70% 的韭菜。进入股市买卖的都觉得自己是高手，最后亏得底裤都没了。 今天我们从一个简单的模型来看看短线交易的成功率有多大？

短线交易模型的由来技术图片

所谓短线交易，就是在一个股价的地点买进，然后在几天之内卖出。

A 股大多数交易者都喜欢短线交易，他们都希望今天买入，明天就卖出，以此来赚快钱，殊不知短线交易是大多数人亏损最快的方式。

A 股市场上有一批最顶尖的高手，他们可以做到八年一万倍的神话，这类高手惊人收益率的来源就是短线交易，他们的镰刀专门伸向追涨杀跌的韭菜。

正式因为有这群人的存在，A 股还有一个著名的榜单，叫做“龙虎榜”。

沪深交易龙虎榜指每日两市中涨跌幅、换手率等由大到小的排名榜单，并从中可以看到龙虎榜单中的股票在哪个证券营业部的成交量较大。该数据有助于了解当日异动个股的资金进出情况，判断是游资所为还是机构所为。

我们的短线交易模型就是要从这个龙虎榜说起。 我在浏览东方财富网的龙虎榜时，无意中发现他们有个奇怪的数据，如下图所示：

技术图片

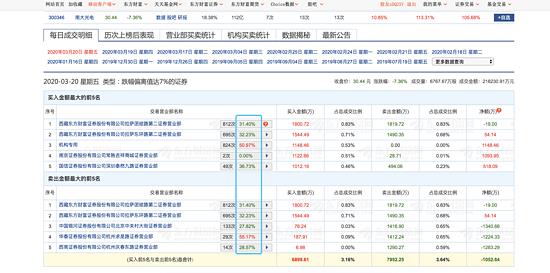
这一栏数据表示的是近三个月内该营业部买入个股后3天个股上涨的概率。

我们都知道股票就是个概率游戏，如果我能够计算出一只股票的上涨概率，那么我就能根据概率来进行博弈了。如果我每次买入之后上涨的概率大于50%，那么每次下注的话，长期来看，稳赢啊！

我越想越兴奋，感觉发现了一座金矿！

我的脑海中顿时闪现了一个思路：根据每个营业部买入后3天个股上涨的概率以及营业部买入的金额占总买入金额的比例，我计算出每只上榜股票后面3天上涨的概率。

具体的步骤如下：

  1. 先将买入的营业部买入净额排序，换算成比例，例如：买入1:买入2:买入3:买入4:买入5=a 技术图片 c:d:e；
  2. 查看营业部上榜后的上涨概率，例如为：A,B,C,D,E；
  3. 查看营业部上榜后的平均涨幅，例如为：A1,B1,C1,D1,E1；
  4. 计算综合上涨概率，公式为：(a A+b B+c C+d D+e*E)/(a+b+c+d+e)
  5. 计算综合涨幅，公式为：(a A1+b B1+c C1+d D1+e*E1)/(a+b+c+d+e)
  6. 计算得到的概率值越大越好，越大越值得搏击

数据准备

以上只是初步设想的一个简单模型，要进行实践，我们首先必须用历史数据来验证，看看这个模型是否可靠。

要验证这个模型的可靠性，我们需要龙虎榜数据和个股行情数据。

下面简单介绍一下这两个数据的获取方法。

龙虎榜数据

我们从东方财富的网页上来获取龙虎榜数据：http://data.eastmoney.com/stock/tradedetail/2020-03-20.html ，打开页面如下：

技术图片

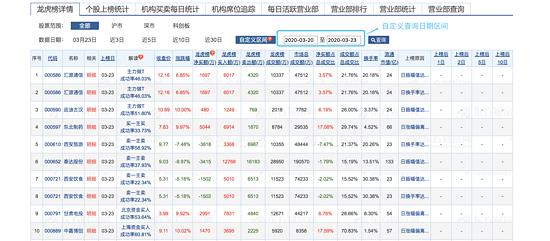
这个页面可以自定义查询日期区间，这就很方便的查询一段时间的数据了。

我们接着打开开发者工具，点击查询，就可以很容易地找到查询数据的请求：

技术图片

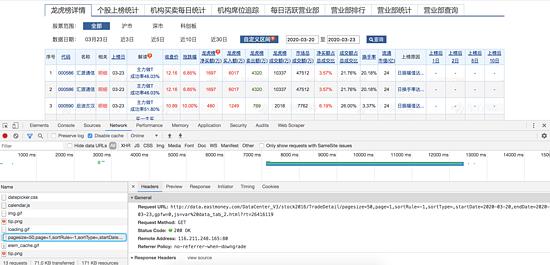
我们获取到的请求为：

http://data.eastmoney.com/DataCenter_V3/stock2016/TradeDetail/pagesize=50,page=1,sortRule=-1,sortType=,startDate=2020-03-20,endDate=2020-03-23,gpfw=0,js=var%20data_tab_2.html?rt=26416119

在请求中，你可以带上开始和结束日期，将pagesize设置大一些，就可以一次性将一段时间的数据查询出来。

这里就是一个简单的 requests 请求，请求获取的数据也可以很方便的解析，我就不放代码了。

请求到龙虎榜的列表后，我们就可以查询每一个股票的龙虎榜详情数据了，我们点击列表中的“明细”，就可以跳到龙虎榜详情页面了，对应的 URL 为：http://data.eastmoney.com/stock/lhb,2020-03-23,002727.html

我们使用 requests 请求这个 URL，就可以获取到这个页面的 HTML 内容，然后解析 HTML 内容即可得到龙虎榜详情数据。

解析的核心代码如下：

def parse_data(self, html, lhb_date, scode):
        pattern_all = re.compile(‘ [sS]*?<div class="content-sepe">[sS]*?<table cellpadding="0" cellspacing="0" class="default_tab stock-detail-tab" id="tab-2">[sS]*?</thead>[sS]*?<tbody>([sS]*?)</tbody>[sS]*?</table>[sS]*?<table cellpadding="0" cellspacing="0" class="default_tab tab-2" id="tab-4">[sS]*?</thead>[sS]*?<tbody>([sS]*?)</tbody>[sS]*?</table>[sS]*?</div>[sS]*?数据来源[sS]*?‘)
        all_content = re.findall(pattern_all, html)
        #print(all_content[0][1])

        obj_list=[]
        if len(all_content):
            buy_content = str(all_content[0][0])
            sell_content = str(all_content[0][1])

            buy_objs = self.parse_detail(buy_content, 0, lhb_date, scode)
            sell_objs = self.parse_detail(sell_content, 1, lhb_date, scode)
            obj_list.extend(buy_objs)
            obj_list.extend(sell_objs)

        return obj_list

    def parse_detail(self, content, type, lhb_date, scode):
        pattern = re.compile(‘[sS]*?<tr>[sS]*?<div class="sc-name">[sS]*?<a href=""><a href="/stock/([sS]*?).html">([sS]*?)</a></a>[sS]*?<div class="times-percent[sS]*?<div class="left">[sS]*?<span class="times">([sS]*?)</span><span[sS]*?>([sS]*?)</span>[sS]*?<div class="right">[sS]*?<td[sS]*?>([sS]*?)</td>[sS]*?<td>([sS]*?)</td>[sS]*?<td[sS]*?>([sS]*?)</td>[sS]*?<td[sS]*?>([sS]*?)</td>[sS]*?<td[sS]*?>([sS]*?)</td>[sS]*?</tr>[sS]*?‘)
        items = re.findall(pattern, content)
        obj_list=[]
        for item in items:
            obj = {}
            obj[‘sales_code‘] = self.clear_quote(item[0]) #营业部code
            obj[‘sales_name‘] = self.clear_quote(item[1]) #营业部名称
            obj[‘his_rank_times‘] = NumUtils.trans_int(self.clear_quote(item[2])) #历史上榜次数
            obj[‘his_rank_rate‘] = NumUtils.trans_float(self.clear_quote(item[3])) #历史买入3天上涨概率
            obj[‘buy_money‘] = NumUtils.trans_float(self.clear_quote(item[4])) #买入额
            obj[‘buy_of_total_rate‘] = NumUtils.trans_float(self.clear_quote(item[5])) #买入额占成交额比例
            obj[‘sell_money‘] = NumUtils.trans_float(self.clear_quote(item[6])) #卖出额
            obj[‘sell_of_total_rate‘] = NumUtils.trans_float(self.clear_quote(item[7])) #卖出额占成交额比例
            obj[‘net_money‘] = NumUtils.trans_float(self.clear_quote(item[8])) #净买入额
            obj[‘type‘] = type #买卖类型，0-买入，1-卖出
            obj[‘tdate‘] = lhb_date
            obj[‘scode‘] = scode
            obj_list.append(obj)

        return obj_list

通过这两步，我们的龙虎榜数据就得到了，我们把它存储到数据库。

个股详情数据

由于没有地方可以一次性获取到一段时间的个股数据，但是我们可以在东方财富网站上以找到当天所有个股的行情数据，URL 为：http://quote.eastmoney.com/center/gridlist.html#hs_a_board ，所以这个只能每天获取一次，然后累积一段时间了。

这个个股详情数据页面如下：

技术图片

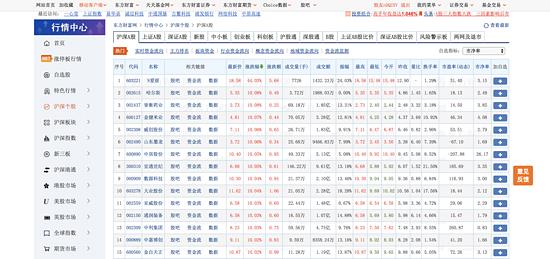
跟龙虎榜列表页面一样，我们可以很容易地找到获取数据的请求：

技术图片

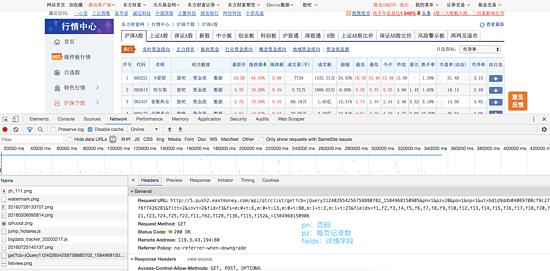
请求里面的主要参数有三个：

pn：页码

pz：每页记录数

fields：个股详情字段

同样地，我们可以将每页记录数设置足够大，以确保一次性获取所有个股数据。

获取方式很简单，我们就不贴代码了。但是有一点需要注意，这个个股数据是实时的，所以我们得每天收盘（下午三点）过后再获取，才能得到收盘数据。

回溯验证

每日选股

根据我们前面所讲的模型的步骤，我们的选股核心代码如下：

def ana(self, detail_list):
        scode_dict = {}
        rank_list = []
        for detail in detail_list:
            if detail[‘scode‘] not in scode_dict.keys():
                sub_list = [detail]
                scode_dict[detail[‘scode‘]] = sub_list
            else:
                sub_list = scode_dict[detail[‘scode‘]]
                sub_list.append(detail)
                scode_dict[detail[‘scode‘]] = sub_list

        for key in scode_dict.keys():
            scode = key
            sub_list = scode_dict[key]
            # 总买入额
            total_money = float(0)
            # 营业部上涨概率
            yyb_avg_rate_list = []
            for detail in sub_list:
                total_money = total_money + float(detail[‘buy_money‘])
                yyb_avg_rate_list.append(float(detail[‘his_rank_rate‘]))

            # 买入额占比
            money_rate_list = [float(item[‘buy_money‘])/total_money for item in sub_list]
            total_rate = float(0)
            for i in range(0, len(sub_list)):
                total_rate = float(total_rate) + float(yyb_avg_rate_list[i] * money_rate_list[i])
            rank_list.append({‘scode‘: scode, ‘total_rate‘: total_rate})

        rank_list.sort(key=lambda it: it.get(‘total_rate‘), reverse=True)
        return rank_list

这里是严格按照前面的步骤来做的，最后将结果按照上涨概率倒序排列。

计算选股的上涨幅度

从龙虎榜中按照上涨概率将个股排序后，我准备选取最大上涨概率的股票来进行回溯。如果最大上涨概率的股票第二天开盘直接涨停，那么舍弃，再选择第二大概率的，以此类推。

由于股票的买卖价位决定了收益率的高低，我们无法知道真实操作中的买卖价格，所以这里我用三种策略来进行对比：

乐观值：第一天最低价买进，第二天最高价卖出。

悲观值：第一天最高价买进，第二天最低价卖出。

平均值：第一天平均价买进，第二天平均价卖出。

由于我们的上涨概率是上榜后3天的上涨概率，所以我们的买卖方式可能是：

第一天买入，第二天卖出；

第一天买入，第三天卖出；

第二天买入，第三天卖出。

这里我把上述情况归结为两种：第一天买入第二天卖出和前两天某一天买入第三天卖出。

根据上面的思路，我们的核心代码为：

def compute(self, date, stat_type):
        ### stat_type 表示统计类型，1-计算两天，2-计算三天 ###
        # 1. 获取每日的龙虎榜选股(根据概率倒序)
        lhbpick = lhb_history_pick.lhbHisPick()
        pick_list = lhbpick.deal(date)

        if not len(pick_list):
            return None

        # 2. 根据选股计算上涨点数
        for stock in pick_list:
            # 将退市警示股和新股排除
            if ‘ST‘ in stock[‘name‘] or ‘*ST‘ in stock[‘name‘] or ‘N‘ in stock[‘name‘]:
                continue

            # 获取股票三日行情数据
            stock_day_detail = self.query_stock_detail(stock[‘scode‘], date)
            # 选股当天收盘价
            day_close_price = stock_day_detail[0][‘close_price‘]
            # 选股后一天涨停价
            first_day_limit = stock_utils.StockUtils.calc_limit_price(day_close_price)
            # 选股后一天最低价
            first_day_low_price = stock_day_detail[1][‘low_price‘]
            # 选股后一天最高价
            first_day_top_price = stock_day_detail[1][‘top_price‘]
            # 选股后一天开盘价
            first_day_open = stock_day_detail[1][‘open_price‘]
            # 选股后一天平均价
            first_day_avg_price = (first_day_top_price + first_day_low_price) / 2
            # 开盘即涨停并且一天未开板，买不进，放弃
            if first_day_low_price == first_day_top_price or first_day_limit == first_day_open:
                continue

            # 选股后二天最低价
            second_day_low_price = stock_day_detail[2][‘low_price‘]
            # 选股后二天最高价
            second_day_top_price = stock_day_detail[2][‘top_price‘]
            # 选股后二天平均价
            second_day_avg_price = (second_day_top_price + second_day_low_price) / 2

            # 计算上榜后两天的情况
            optim_up2 = (second_day_top_price - first_day_low_price) / first_day_low_price
            pessim_up2 = (second_day_low_price - first_day_top_price) / first_day_top_price
            avg_up2 = (second_day_avg_price - first_day_avg_price) / first_day_avg_price

            if stat_type == 1:
                # print(optim_up2, pessim_up2, avg_up2)
                return optim_up2, pessim_up2, avg_up2

            # 选股后三天最低价
            third_day_low_price = stock_day_detail[3][‘low_price‘]
            # 选股后三天最高价
            third_day_top_price = stock_day_detail[3][‘top_price‘]
            # 选股后三天平均价
            third_day_avg_price = (second_day_top_price + second_day_low_price) / 2

            # 计算上榜后三天的情况
            max2 = max(first_day_top_price, second_day_top_price)
            min2 = min(first_day_low_price, second_day_low_price)
            avg2 = (first_day_avg_price + second_day_avg_price) / 2

            optim_up3 = (third_day_top_price - min2) / min2
            pessim_up3 = (third_day_low_price - max2) / max2
            avg_up3 = (third_day_avg_price - avg2) / avg2

            return optim_up3, pessim_up3, avg_up3

        return None

通过上述方法，我们就获得了某一天所选出的股票的后三天上涨的幅度。

结果展示

我准备从三段不同趋势的行情来验证模型，分别是趋势上涨，趋势震荡，趋势下跌三种。

选取的时间周期都是一周，对应的大盘指数日K图如下：

技术图片

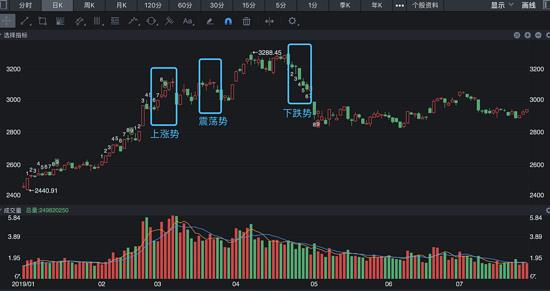
为了更直观地展示效果，我将每个周期的上涨幅度用折线图来展示。

我们来看看上涨趋势的收益图：

技术图片

技术图片

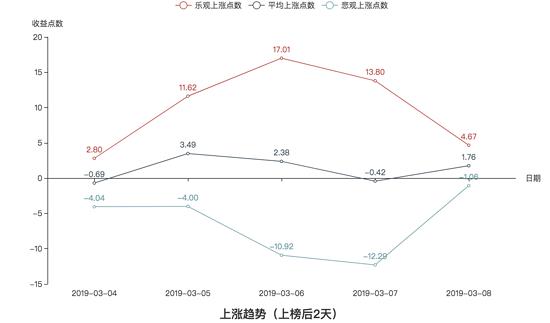
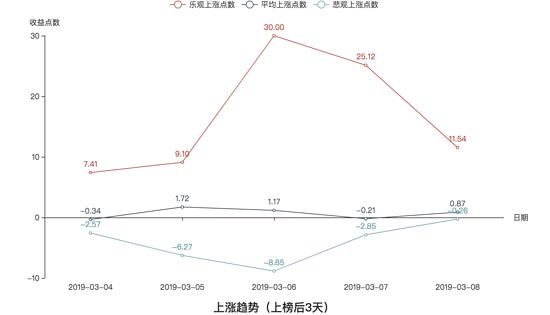
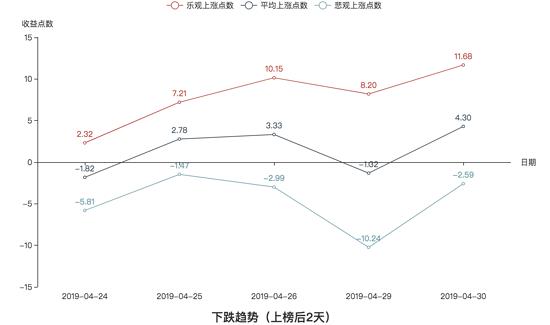
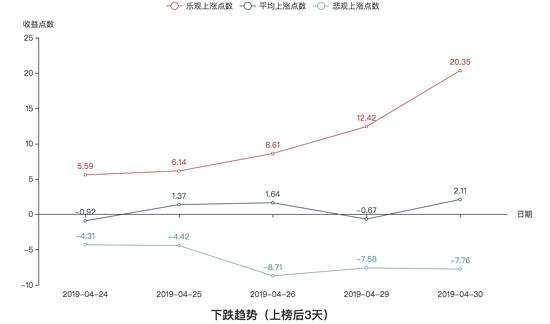
下跌趋势的收益图：

技术图片

技术图片

震荡趋势的收益图：

技术图片

技术图片

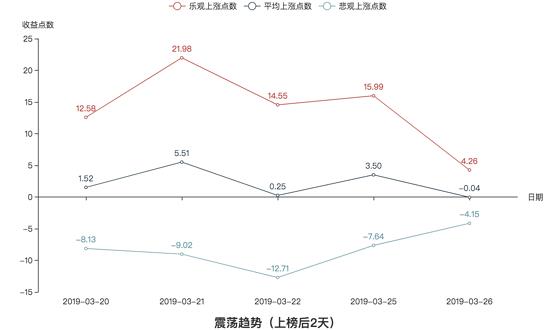
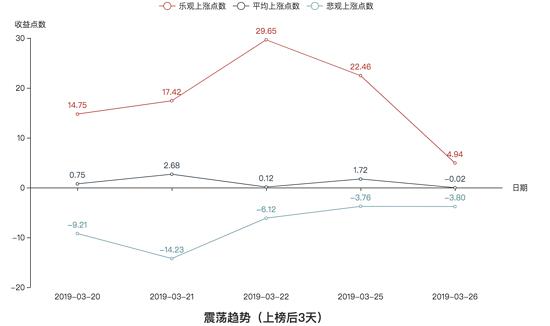
我们先来进行纵向对比，很明显，不论在哪种趋势下，收益率的关系都是：乐观 > 平均 > 悲观。这也跟我们的常理相吻合，毕竟乐观和悲观是两种极端操作方法，而平均是介于这两者极端之间的。

我们再从上榜后2天和上榜后3天的方面来对比，我们可以看到，不论在哪种趋势下，上榜后3天的总体收益率比上榜后两天高，这也应该可以事先预想到。

接着，我们可以看到三种趋势下总体收益率的情况：三种趋势下，收益率并没有跟随不同的趋势而出现显著的特点，所以在三种趋势下，最大上涨概率的股票收益率没有显著的区别。换句话说，就是不管在何种趋势下，最好的短线操作都可以赚到差不多的收益。

我们来总结一下：如果你是市场上顶尖的选手，可以买在最低价卖在最高价，那么不论行情怎么样，你都可以获取不菲的收益；如果你是追涨杀跌型的韭菜，那么你做短线注定会亏损；如果你只是平均水平，那么你的收益很微薄，所以要想参与短线操作，你的水平至少必须在平均水平以上。

当然，股票市场上的变量很多，这只是一个简单的模型，考虑的变量也很少，而且验证的数据也相对较少，只能大致说明短线操作的收益情况，并不是严谨的论证。

以上是关于短线买股赚钱的概率有多大？python带你来分析的主要内容，如果未能解决你的问题，请参考以下文章

数据分析 | 浙江省考你上岸概率有多大！

AI大牛李沐带你来装机！你也能练100亿的大模型

解析隐式类型转换操作operator double() const，带你了解隐式转换危害有多大

网红代运营网红有多大的商业价值？

图机器学习有多大神力？一文带你回顾2020，展望2021

混检阳性概率的计算（贝叶斯定理的一个应用例）