[Python] 数据结构--实现顺序表链表栈和队列
Posted 蜗牛噢
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[Python] 数据结构--实现顺序表链表栈和队列相关的知识,希望对你有一定的参考价值。
说明:
本文主要展示Python实现的几种常用数据结构:顺序表、链表、栈和队列。
附有实现代码。
来源主要参考网络文章。
一、顺序表
1、顺序表的结构
一个顺序表的完整信息包括两部分,一部分是表中元素集合,另一部分是为实现正确操作而需记录的信息,即有关表的整体情况的信息,这部分信息主要包括元素存储区的容量和当前表中已有的元素个数两项。

2、顺序表的两种基本实现方式
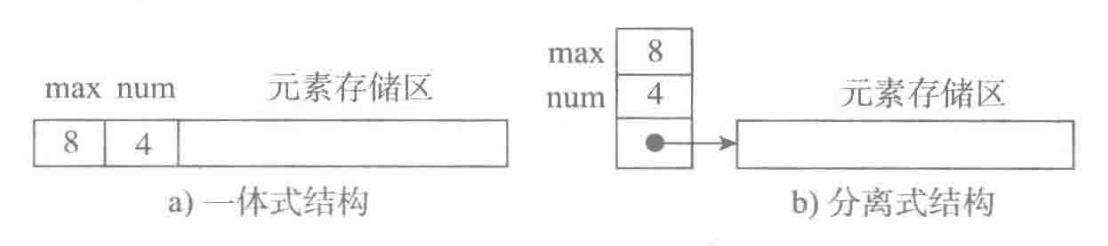
图a 为一体式结构,存储表信息的单元与元素存储区以连续的方式安排在一块存储区里,两部分数据的整体形成一个完整的顺序表对象。一体式结构整体性强,易于管理。但是由于数据元素存储区域是表对象的一部分,顺序表创建后,元素存储区就固定了。
图b 为分离式结构,表对象里只保存与整个表有关的信息(容量和元素个数),实际数据元素存放在另一个独立的元素存储区里,通过链接与基本表对象关联。
3、元素存储区替换
一体式结构由于顺序表信息区与数据区联系存储在一起,所以若想更换数据区,则只能整体搬迁,即整个顺序表对象(指存储顺序表的结构信息的区域)改变了。
分离式结构若想更换数据区,只需将表信息区中的数据区链接地址更新即可,而该顺序表对象不变。
4、元素存储区扩充及其策略
分离式结构的顺序表,如想将数据区更换为存储空间更大的区域,则可以在不改变表对象的前提下对其数据存储区进行了扩充,所有使用这个表的地方都不必修改。只要程序的运行环境(计算机系统)还有空闲存储,这种表结构就不会因为满了而导致操作无法进行。人们把采用这种技术实现的顺序表称为动态顺序表,因为其容量可以在使用中动态变化。
扩充的两种策略:
》每次扩充增加固定数目的存储位置,如每次扩充10个元素位置,这种策略可称为线性增长。
(特点:节省空间,但是扩充操作频繁,操作次数多)
》每次扩充容量加倍,如每次扩充增加一倍存储空间。
(特点:减少了扩充操作的执行次数,但可能会浪费空间资源。以空间换时间,推荐的方式)
》Python的官方实现中,list 实现采用了如下的策略:在建立空表(或很小的表)时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大(目前阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式,是为了避免出现过多的空闲的存储位置。
5、顺序表的操作
增加元素,下图为顺序表增加元素的三种方式:
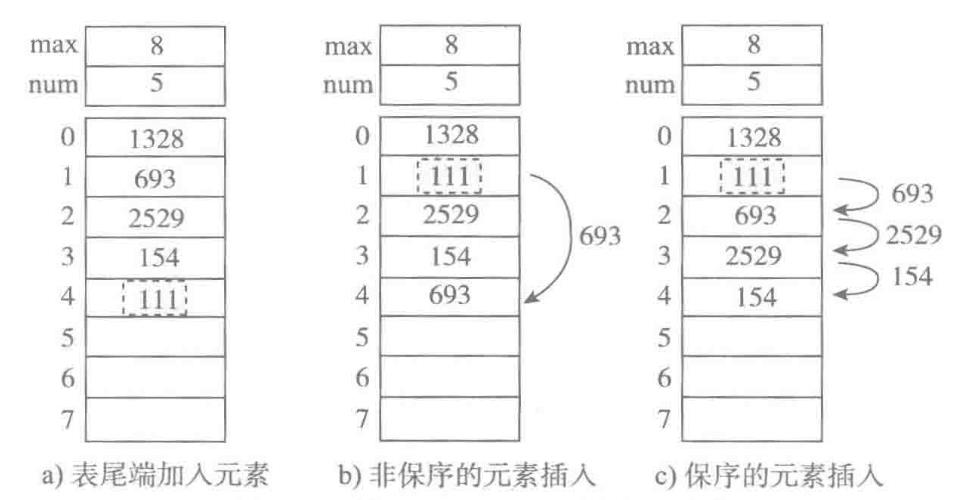
a、尾端加入元素,时间复杂度为 O(1)
b、非保序的加入元素(不常见)没时间复杂度为 O(1)
c、保序的元素加入,时间复杂度为 O(n)
删除元素,下图为顺序表删除元素的三种方式:
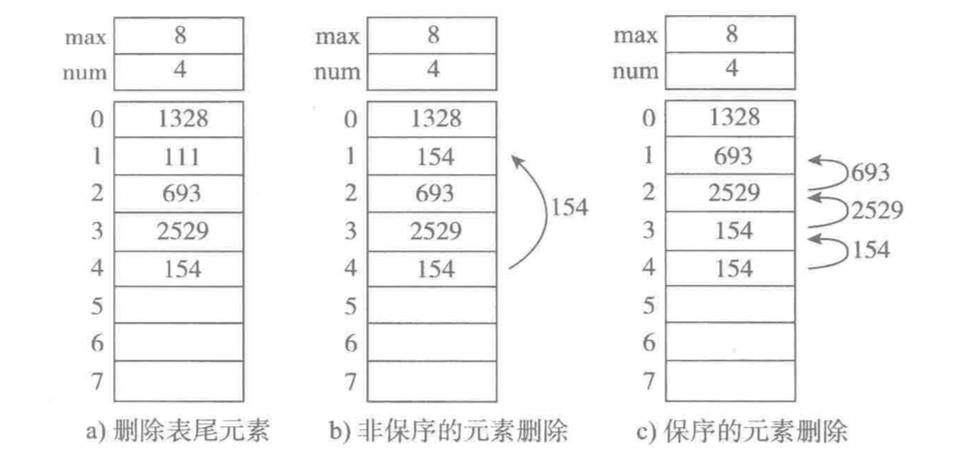
a、删除表尾元素,时间复杂度为 O(1)
b、非保序的元素删除(不常见),时间复杂度为 O(1)
c、保序的元素删除,时间复杂度为 O(n)
6、Python 中的顺序表
Python中的 list 和 tuple 两种类型采用了顺序表的实现技术,具有前面讨论的顺序表的所有性质。
tuple是不可变类型,即不变的顺序表,因此不支持改变其内部状态任何操作,而其他方面,则与list的性质类似。
list的基本实现技术:
Python表中类型list就是一种元素个数可变的线性表,可以加入和删除元素,并在各种操作维持已有元素顺序(即保序),而且还具有以下行为特征:
》基于下标(位置)的高效元素访问和更新,时间复杂度应该是 O(1);
为满足该特征,应该采用顺序表技术,表中元素保存在一块连续的存储区中。
》允许任意加入元素,而且在不断加入元素的过程中,表对象的标识(函数id得到的值)不变
为满足该特征,就必须能更换元素存储区,并且为保证更换存储区时list对象的标识id不变,只能采用分离式实现技术。
在Python官方实现中,list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x)(或list.insert(len(list), x), 即尾部插入)比在指定位置插入元素效率高的原因。
二、链表
相对于顺序表,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理,因为顺序表的结构需要预先知道数据大小来申请连续的存储空间,而在进行扩充时又需要进行数据的搬迁。
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是不像顺序表一样连续存储数据,而是每一个结点(数据存储单元)里存放下一个结点的信息(即地址):

1、单向链表
单向链表也叫单链表,是表中最简单的一种形式,它的每个节点包含两个域,一个信息域(元素域)和一个链接域。这个链接指向链表中的下一个节点,而最后一个节点的链接域则指向一个空值。
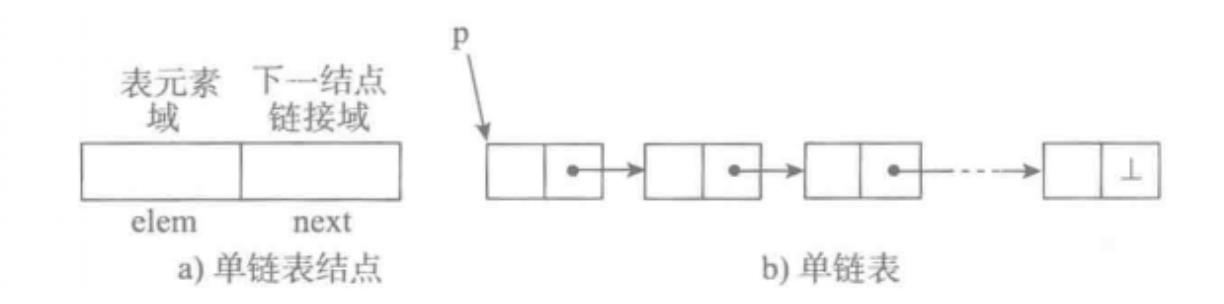
表中元素elem用来存放具体的数据。
链接域next用来存放下一个节点的位置(Python中的标识)。
变量p指向链表的头节点(首节点)的位置,从p出发能找到表中的任意节点。
单链表的操作:
is_empty():链表是否为空
length():链表长度
travel():遍历整个链表
add(item):链表头部添加元素
append(item):链表尾部添加元素
insert(pos, item):指定位置添加元素
remove(item):删除节点
search(item):查找节点是否存在
代码实现:
1 # coding=utf-8 2 # 单链表的实现 3 4 5 class SingleNode: 6 """单链表的节点""" 7 def __init__(self, item): 8 # item存放数据元素 9 self.item = item 10 # 下一个节点 11 self.next = None 12 13 def __str__(self): 14 return str(self.item) 15 16 17 class SingleLinkList: 18 """单链表""" 19 def __init__(self): 20 self._head = None 21 22 def is_empty(self): 23 """判断链表是否为空""" 24 return self._head is None 25 26 def length(self): 27 """获取链表长度""" 28 cur = self._head 29 count = 0 30 while cur is not None: 31 count += 1 32 # 将cur后移,指向下一个节点 33 cur = cur.next 34 return count 35 36 def travel(self): 37 """遍历链表""" 38 cur = self._head 39 while cur is not None: 40 print(cur.item) 41 cur = cur.next 42 print("") 43 44 def add(self, item): 45 """链表头部添加元素""" 46 node = SingleNode(item) 47 48 node.next = self._head 49 self._head = node 50 51 def append(self, item): 52 """链表尾部添加元素""" 53 node = SingleNode(item) 54 55 if self.is_empty(): 56 self._head = node 57 else: 58 cur = self._head 59 while cur.next is not None: 60 cur = cur.next 61 62 # 此时cur指向链表最后一个节点,即 next = None 63 cur.next = node 64 65 def insert(self, pos, item): 66 """指定位置添加元素""" 67 # 若指定位置pos为第一个元素之前,则执行头部插入 68 if pos <= 0: 69 self.add(item) 70 71 # 若指定位置超过链表尾部,则执行尾部插入 72 elif pos > (self.length() - 1): 73 self.append(item) 74 75 # 找到指定位置 76 else: 77 node = SingleNode(item) 78 cur = self._head 79 cur_pos = 0 80 while cur.next is not None: 81 # 获取需要插入位置的上一个节点 82 if pos - 1 == cur_pos: 83 node.next = cur.next 84 cur.next = node 85 cur = cur.next 86 cur_pos += 1 87 88 def remove(self, item): 89 """删除节点""" 90 cur = self._head 91 while cur is not None: 92 if cur.next.item == item: 93 cur.next = cur.next.next 94 break 95 cur = cur.next 96 97 def search(self, item): 98 """查找节点是否存在""" 99 cur = self._head 100 count = 0 101 while cur is not None: 102 if cur.item == item: 103 return count 104 cur = cur.next 105 count += 1 106 107 # 找不到元素 108 if count == self.length(): 109 count = -1 110 return count 111 112 113 if __name__ == "__main__": 114 ll = SingleLinkList() 115 ll.add(1) # 1 116 ll.add(2) # 2 1 117 ll.append(3) # 2 1 3 118 ll.insert(2, 4) # 2 1 4 3 119 print("length:", ll.length()) # 4 120 ll.travel() # 2 1 4 3 121 print("search(3):", ll.search(3)) # 3 122 print("search(5):", ll.search(5)) # -1 123 ll.remove(1) 124 print("length:", ll.length()) # 3 125 ll.travel() # 2 4 3
链表与顺序表的对比:
链表失去了顺序表随机读取的优点,同时链表由于增加了节点的指针域,空间开销比较大,但对存储空间的使用要相对灵活。
链表与顺序表的各种操作复杂度如下所示:
| 操作 | 链表 | 顺序表 |
| 访问元素 | O(n) | O(1) |
| 在头部插入/删除 | O(1) | O(n) |
| 在尾部安插入/删除 | O(n) | O(1) |
| 在中间插入/删除 | O(n) | O(n) |
注意:虽然表面看起来复杂度都是 O(n),但是链表和顺序表在插入和删除时进行的是完全不同的操作。链表的主要耗时操作是遍历查找,删除和插入操作本身的复杂度是O(1)。顺序表查找很快,主要耗时的操作是拷贝覆盖。因为除了目标元素在尾部的特殊情况,顺序表进行插入和删除时需要对操作点之后所有元素进行前后移位操作,只能通过拷贝和覆盖方法进行。
2、单向循环链表
单链表的一个变形是单向循环链表,链表中最后一个节点的next域不再为None,而是指向链表的头结点。

基本操作和单链表基本一样,实现代码如下:
1 # coding=utf-8 2 # 单向循环链表 3 4 5 class Node: 6 """节点""" 7 def __init__(self, item): 8 self.item = item 9 self.next = None 10 11 def __str__(self): 12 return str(self.item) 13 14 15 class SinCycLinkedList: 16 """单向循环链表""" 17 def __init__(self): 18 self._head = None 19 20 def is_empty(self): 21 """判断链表是否为空""" 22 return self._head is None 23 24 def length(self): 25 """链表长度""" 26 if self.is_empty(): 27 return 0 28 count = 1 29 cur = self._head 30 while cur.next != self._head: 31 # print("cur", cur.item) 32 count += 1 33 cur = cur.next 34 return count 35 36 def travel(self): 37 """遍历""" 38 if self.is_empty(): 39 return 40 41 cur = self._head 42 print(cur.item) 43 while cur.next != self._head: 44 cur = cur.next 45 print(cur.item) 46 47 def add(self, item): 48 """在头部添加一个节点""" 49 node = Node(item) 50 if self.is_empty(): 51 self._head = node 52 node.next = self._head 53 else: 54 node.next = self._head 55 cur = self._head 56 while cur.next != self._head: 57 cur = cur.next 58 59 cur.next = node 60 self._head = node 61 62 def append(self, item): 63 """在尾部添加一个节点""" 64 node = Node(item) 65 if self.is_empty(): 66 self._head = node 67 node.next = self._head 68 else: 69 cur = self._head 70 # print(type(cur), cur.item, cur.next) 71 while cur.next != self._head: 72 cur = cur.next 73 74 # print(cur.item) 75 cur.next = node 76 node.next = self._head 77 78 def insert(self, pos, item): 79 """指定位置pos添加节点""" 80 if pos <= 0: 81 self.add(item) 82 elif pos > (self.length() - 1): 83 self.append(item) 84 else: 85 node = Node(item) 86 cur = self._head 87 cur_pos = 0 88 while cur.next != self._head: 89 if (pos - 1) == cur_pos: 90 node.next = cur.next 91 cur.next = node 92 break 93 cur_pos += 1 94 cur = cur.next 95 96 def remove(self, item): 97 """删除一个节点""" 98 if self.is_empty(): 99 return 100 101 pre = self._head 102 # 删除首节点 103 if pre.item == item: 104 cur = pre 105 while cur.next != self._head: 106 cur = cur.next 107 108 cur.next = pre.next # 删除首节点(跳过该节点) 109 self._head = pre.next # 重新指定首节点 110 111 # 删除其他的节点 112 else: 113 cur = pre 114 while cur.next != self._head: 115 if cur.next.item == item: 116 cur.next = cur.next.next 117 cur = cur.next 118 119 def search(self, item): 120 """查找节点是否存在""" 121 if self.is_empty(): 122 return -1 123 124 cur_pos = 0 125 cur = self._head 126 if cur.item == item: 127 return cur_pos 128 129 while cur.next != self._head: 130 if cur.item == item: 131 return cur_pos 132 cur_pos += 1 133 cur = cur.next 134 135 if cur_pos == self.length() - 1: 136 return -1 137 138 139 if __name__ == "__main__": 140 ll = SinCycLinkedList() 141 ll.add(1) # 1 142 ll.add(2) # 2 1 143 # ll.travel() 144 ll.append(3) # 2 1 3 145 ll.insert(2, 4) # 2 1 4 3 146 ll.insert(4, 5) # 2 1 4 3 5 147 ll.insert(0, 6) # 6 2 1 4 3 5 148 print("length:", ll.length()) # 6 149 ll.travel() # 6 2 1 4 3 5 150 print("search(3)", ll.search(3)) # 4 151 print("search(7)", ll.search(7)) # -1 152 print("search(6)", ll.search(6)) # 0 153 print("remove(1)") 154 ll.remove(1) 155 print("length:", ll.length()) # 6 2 4 3 5 156 print("remove(6)") 157 ll.remove(6) 158 ll.travel()
3、双向链表
一种更复杂的链表是 "双向链表" 或 "双面链表"。每个节点有两个链接:一个指向前一个节点,当次节点为第一个节点时,指向空值;而另一个指向下一个节点,当此节点为最后一个节点时,指向空值。
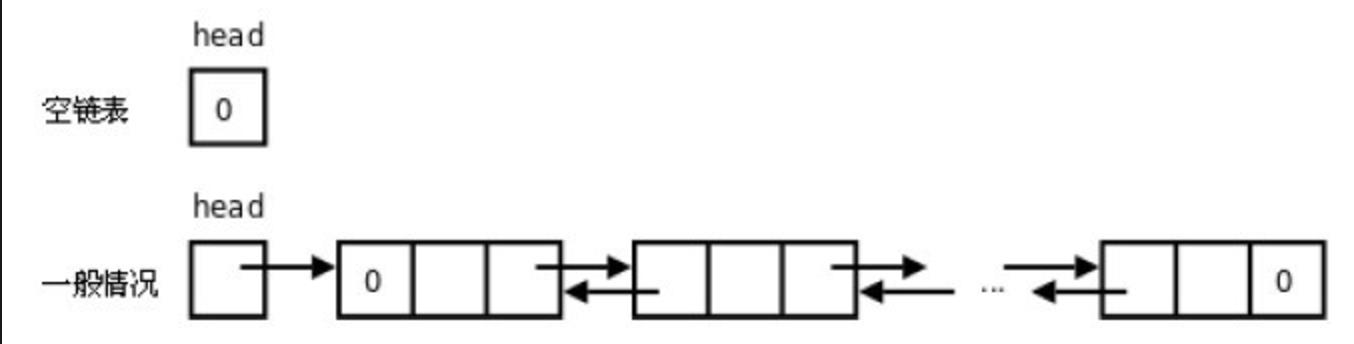
基本操作和单链表一样,不同的实现,代码如下:
1 # coding=utf-8 2 # 双向链表 3 4 5 class Node: 6 """节点""" 7 def __init__(self, item): 8 self.item = item 9 self.prev = None 10 self.next = None 11 12 13 class DLinkList: 14 """双向链表"""以上是关于[Python] 数据结构--实现顺序表链表栈和队列的主要内容,如果未能解决你的问题,请参考以下文章