什么是调整后的R方
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了什么是调整后的R方相关的知识,希望对你有一定的参考价值。
spss线性回归分析中模型汇总中分为“R方”和“调整后的R方”,有什么区别??
1、调整R方的解释与R方类似,不同的是:调整R方同时考虑了样本量(n)和回归中自变量的个数(k)的影响,这使得调整R方永远小于R方,而且调整R方的值不会由于回归中自变量个数的增加而越来越接近1。
因此,在多元回归分析中,通常用调整的多重判定系数来评价拟合效果。
2、R方的平方根称为多重相关系数,也称为复相关系数,它度量了因变量同k个自变量的相关程度。
注:SPSS中进行相关分析,一般只能得到两两之间的相关系数,因此,若要求复相关系数,可在多元回归中实现!
区别是系数不同。自变量个数的增加将影响到因变量中被回归方程所解释的变异比例,即会影响判定系数(R方)的大小。当增加自变量时,会使残差平方和减少,从而使R方变大。
如果模型中增加一个自变量,即使这个自变量在统计上并不显著,R方也会变大。因此,为避免增加自变量而高估R方,统计学家提出用样本量(n)和自变量的个数(k)去调整R方,计算出调整的多重判定系数(调整的R方)。

扩展资料
例如:当给模型增加自变量时,复决定系数也随之逐步增大,当自变量足够多时总会得到模型拟合良好,而实际却可能并非如此。于是考虑对R2进行调整,记为Ra2,称调整后复决定系数。
R2=SSR/SST=1-SSE/SST
Ra2=1-(SSE/dfE)/(SST/dfT)
参考资料来源:百度百科-固定R平方
参考技术A 当给模型增加自变量时,复决定系数也随之逐步增大,当自变量足够多时总会得到模型拟合良好,而实际却可能并非如此。于是考虑对R2进行调整,记为Ra2,称调整后复决定系数。R2=SSR/SST=1-SSE/SST
Ra2=1-(SSE/dfE)/(SST/dfT)
详见pdf参考资料 或 《应用回归分析》“自变量选择与回归”章节 或 维基百科Coefficient of determination词条
参考资料:http://bus.utk.edu/stat/Stat538/ClassMaterials/Adjusted%20R2.pdf
本回答被提问者采纳 参考技术B R^2=SSE/SST=1-SSR/SST全说反了= =
译:支持向量机(SVM)及其参数调整的简单教程(Python和R)
一、介绍
数据分类是机器学习中非常重要的任务。支持向量机(SVM)广泛应用于模式分类和非线性回归领域。 SVM算法的原始形式由Vladimir N.Vapnik和Alexey Ya提出。自从那以后,SVM已经被巨大地改变以成功地用于许多现实世界问题,例如文本(和超文本)分类,图像分类,生物信息学(蛋白质分类,癌症分类),手写字符识别等。
二、目录
什么是支持向量机?
SVM是如何工作的?
推导SVM方程
SVM的优缺点
用Python和R实现
1.什么是支持向量机(SVM)?
支持向量机是一种有监督的机器学习算法,可用于分类和回归问题。它遵循一种用核函数技巧来转换数据的技术,并且基于这些转换,它找到可能输出之间的最佳边界。
简单来说,它做一些非常复杂的数据转换,以找出如何根据标签或输出定义的数据分离。本文我们将看到SVM分类算法。
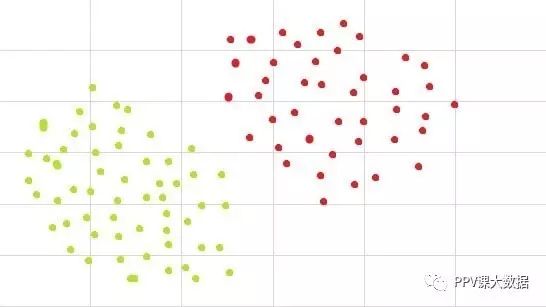
2.SVM是如何工作的?
主要思想是确定最大化训练数据的最佳分离超平面。让我们逐项地来理解这个客观术语。
什么是分离超平面?
我们看到,上图中给出的数据是可以分离的。例如,我们可以绘制一条线,其中线下方的所有点都是绿色的,而线上方的点是红色的。这样的线被称为分离超平面。
这时你可能会疑惑,它是一条线为什么它叫一个超平面?
在上面的图中,我们已经考虑了最简单的示例,即数据集位于2维平面()中。但是支持向量机也可以用于一般的n维数据集。在更高维度的情况下,超平面是平面的概括。
更正式地说,它是n维欧几里德空间的n-1维子空间。所以一个
1维数据集,单点表示超平面。
2维数据集,线是超平面。
3维数据集,平面是超平面。
在更高的维度上,就被称为超平面。
我们已经说SVM的目标是找到最佳分离超平面。那么什么时候分离超平面是最优的?
事实上,存在分离数据集的超平面并不意味着它是最优的。
让我们通过一组图来理解最佳超平面。
1、多重超平面
有多个超平面,但其中哪一个是分离超平面? 可以很容易地看出,线B是最好地分离这两个类的线。
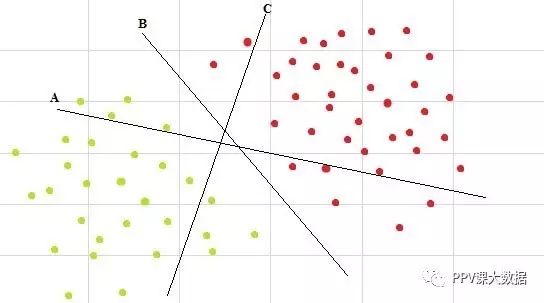
2、多分离超平面
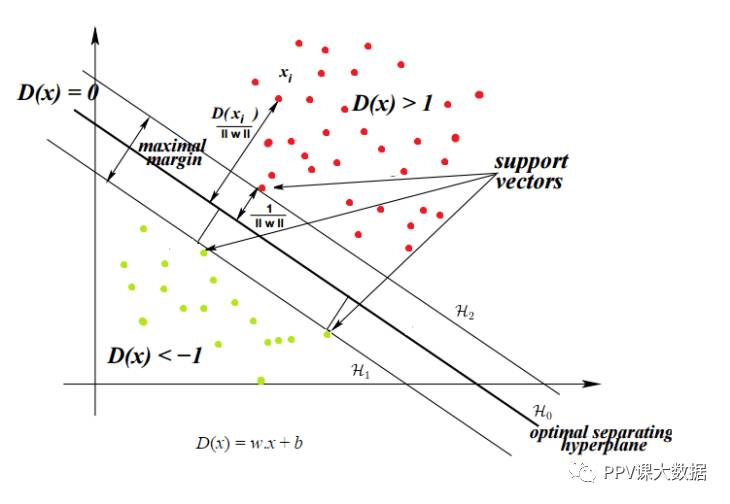
数据集可以有多个分离,我们如何找到最佳的分离超平面? 直观地,如果我们选择接近一个类的数据点的超平面,那么它可能不能很好地推广。因此,要选择尽可能远离每个类别的数据点的超平面。
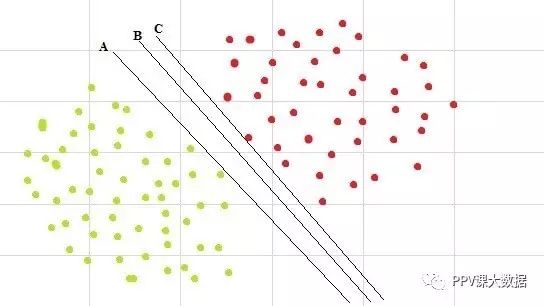
在上图中,满足指定条件的最佳超平面为B。
因此,最大化每个类的最近点和超平面之间的距离就能找到最优分离超平面。这个距离称为边距。
SVM的目标是找到最佳超平面,因为它不仅分类现有数据集,而且有助于预测未知数据的类。最优超平面是边距最大的平面。
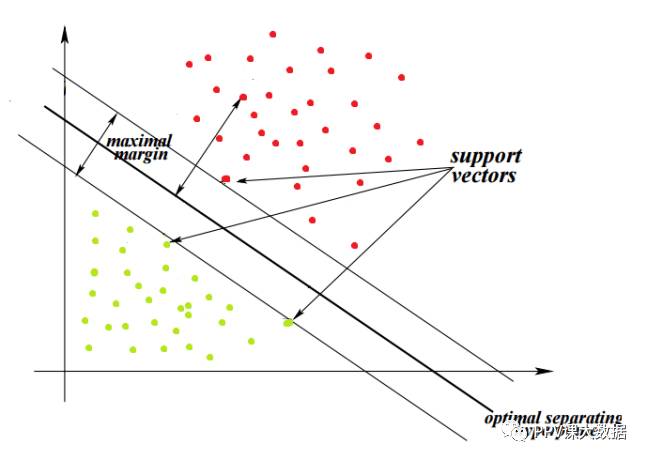
3.推导SVM方程
现在我们已经了解了这个算法的基本组成,让我们直接了解SVM的数学组成。
我将假设你熟悉基本的数学概念,如矢量,矢量算术(加法,减法,点积)和正交投影。这些概念也可以在文章“机器学习线性代数的先决知识”(http://blog.hackerearth.com/prerequisites-linear-algebra-machine-learning)中找到。
超平面方程
你将会看到一条直线方程,如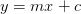 ,其中m是斜率,c是直线在y轴的截距。
,其中m是斜率,c是直线在y轴的截距。
超平面的一般方程如下: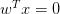
其中 和
和 是向量,
是向量,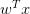 是两个向量的点积。向量
是两个向量的点积。向量 通常被称为权重。
通常被称为权重。
直线方程可化为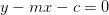 ,这时,
,这时,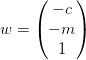 ,
,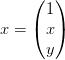
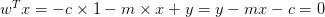
它只是表示同一事物的两种不同的方式。那么为什么我们使用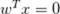
? 简单地,因为在更高维度数据集的情况下该式子更容易处理,并且表示垂直于超平面的向量。 一旦我们开始计算从点到超平面的距离,这个属性将是有用的。
理解约束
我们的分类问题中的训练数据是在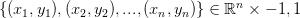 上的。这意味着训练数据集是一对
上的。这意味着训练数据集是一对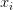 ,
,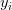 ;
;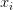 是n维特征向量,
是n维特征向量,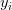 是
是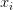 的标签。当
的标签。当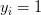 意味着具有特征向量
意味着具有特征向量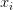 的样本属于类1,并且如果
的样本属于类1,并且如果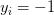 意味着样本属于类-1。
意味着样本属于类-1。
在分类问题中,我们尝试找出一个函数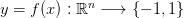 。
。
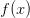 从训练数据集中学习,然后应用其知识来分类未知数据。
从训练数据集中学习,然后应用其知识来分类未知数据。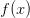 的值可以是无穷大的数,所以我们必须限制我们正在处理的函数类。在SVM的情况下,这类函数是表示为
的值可以是无穷大的数,所以我们必须限制我们正在处理的函数类。在SVM的情况下,这类函数是表示为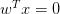 的超平面的函数。
的超平面的函数。
它也可以表示为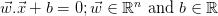
这将输入的空间分成两部分,一部分包含类-1的向量,另一部分包含类+1的向量。
对于本文的其余部分,我们将考虑2维向量。令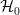 是一个超平面,用于分隔数据集并满足以下条件:
是一个超平面,用于分隔数据集并满足以下条件: 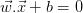 与
与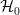 一起,我们可以选择两个其他超平面
一起,我们可以选择两个其他超平面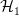 和
和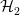 ,使得它们也分离数据并具有以下等式:
,使得它们也分离数据并具有以下等式: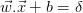 和
和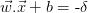
这使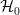 与
与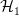 以及
以及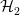 等距。变量δ不是必要的,因此我们可以设置δ=1以简化问题,有
等距。变量δ不是必要的,因此我们可以设置δ=1以简化问题,有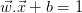 和
和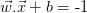 。
。
接下来,我们要确保它们之间没有点。因此,我们将仅选择满足以下约束的超平面:
对于每个向量有:
1、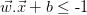 ,
,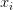 属于类1;
属于类1;
2、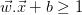 ,
,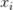 属于类-1。
属于类-1。
组合约束
上述两个约束可以组合成一个约束。
约束1:
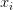 属于类-1,
属于类-1,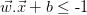 将两边乘以
将两边乘以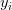 (对于该方程它总是为-1)
(对于该方程它总是为-1)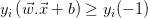 意味着
意味着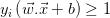 ,因为
,因为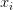 属于类-1。
属于类-1。
约束2:
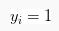
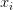 属于类1,
属于类1,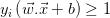
结合上述两个方程,我们得到: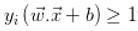 ,对所有的
,对所有的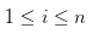
这得到了唯一的约束,而不是在数学上等价的两个约束。组合的新约束也具有相同的效果,即两个超平面之间没有点。
边距最大化
为了简单起见,我们将跳过计算边际的公式的推导,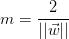
此公式中唯一的变量是 ,它与
,它与 间接成比例,因此边距最大化我们将使
间接成比例,因此边距最大化我们将使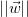
最小,从而得到以下优化问题:
使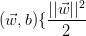 最小,其中
最小,其中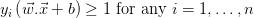
以上是我们的数据是线性可分的情况。在许多情况下,数据不能通过线性分离完全分类。在这种情况下,支持向量机寻找超平面,要最大化边距并最小化错误分类。
为此,我们引入了松弛变量,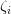 ,它允许一些对象从边缘掉落,但要惩罚他们。
,它允许一些对象从边缘掉落,但要惩罚他们。
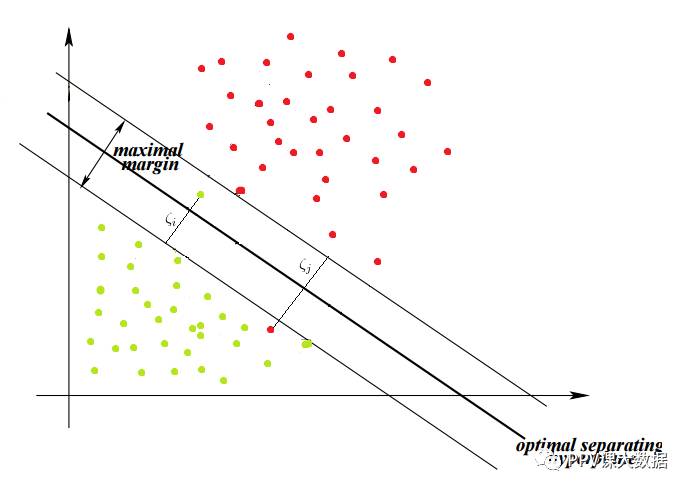
在这种情况下,算法尝试保持松弛变量为零,同时最大化余量。然而,它从边界超平面最小化了错误分类的距离的总和,而不是错误分类的数量。
现在将约束改为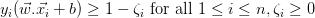 ,将优化问题改为:使
,将优化问题改为:使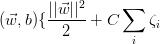 最小化,其中,
最小化,其中,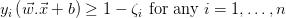
这里,参数C是控制在松弛变量惩罚(错误分类)和边距的宽度之间权衡的正则化参数。
较小的C使得约束容易忽略,这导致大的边距。
较大的C允许约束难以被忽略,这导致小的边距。
对于
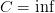 ,强制执行所有约束。
,强制执行所有约束。
分离两类数据的最简单的是在2维数据的情况下的线和在3维数据的情况下的平面。 但是并不可能总是使用线或平面,并且还需要在非线性区域来分离这些类。支持向量机通过使用内核函数来处理这种情况,内核函数将数据映射到不同的空间,其中线性超平面可用于分离类。这被称为核函数技巧,其中内核函数将数据变换到更高维的特征空间,使得线性分离是可能的。
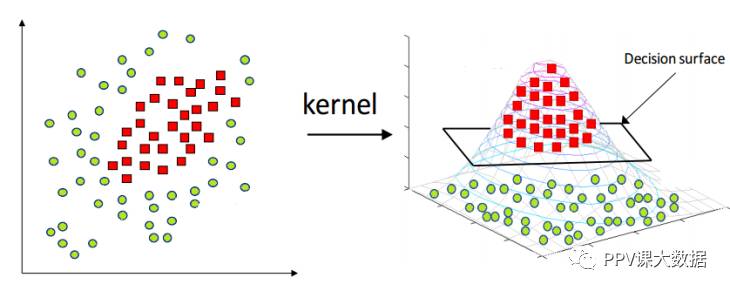
如果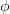 是将
是将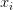 映射到
映射到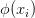 的内核函数,则约束更改为
的内核函数,则约束更改为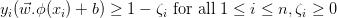
且优化问题为:使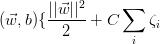 最小化,其中,
最小化,其中,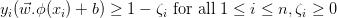
本文我们不讨论这些优化问题的解决方案。 用于解决这些优化问题的最常用的方法是凸优化(Convex Optimization)。
4、支持向量机的优缺点
每个分类算法都有自己的优点和缺点,它们根据正在分析的数据集发挥作用。
SVM的一些优点如下:
凸优化方法的本质是保证最优性。该解决方案保证是全局最小值,而不是局部最小值。
SVM是一种适用于线性和非线性可分离数据(使用核函数技巧)的算法。唯一要做的是找出正则化项C。
SVM在低维和高维数据空间上工作良好。它能有效地对高维数据集工作,因为SVM中的训练数据集的复杂度通常由支持向量的数量而不是维度来表征。即使删除所有其他训练示例并重复训练,我们将获得相同的最佳分离超平面。
SVM可以在较小的训练数据集上工作,因为它们不依赖于整个数据。
SVM的缺点如下:
它们不适合较大的数据集,因为在较大的数据集上使用SVM的训练时间可能很高,并且计算量更大。
它们在具有重叠类的嘈杂数据集上效率较低。
用Python和R实现
让我们来看看用于在Python和R中实现SVM的库和函数。
5、Python实现
在Python中实现机器学习算法的最广泛使用的库是scikit-learn。scikit-learn中用于SVM分类的类是 svm.SVC()
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto')
参数如下:
C:误差项的正则化参数C。
kernel:它指定要在算法中使用的内核类型。它可以是'linear','poly','rbf','sigmoid','precomputed'或callable。 默认值为“rbf”。
degree:它是多项式核函数('poly')的设置,并被所有其他内核忽略。 默认值为3。
gamma:它是'rbf','poly'和'sigmoid的核系数。如果gamma是'auto',则将使用1 / n个特征数。
还有很多高级参数,我在这里没有讨论。你可以点击这里查看(http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC)。
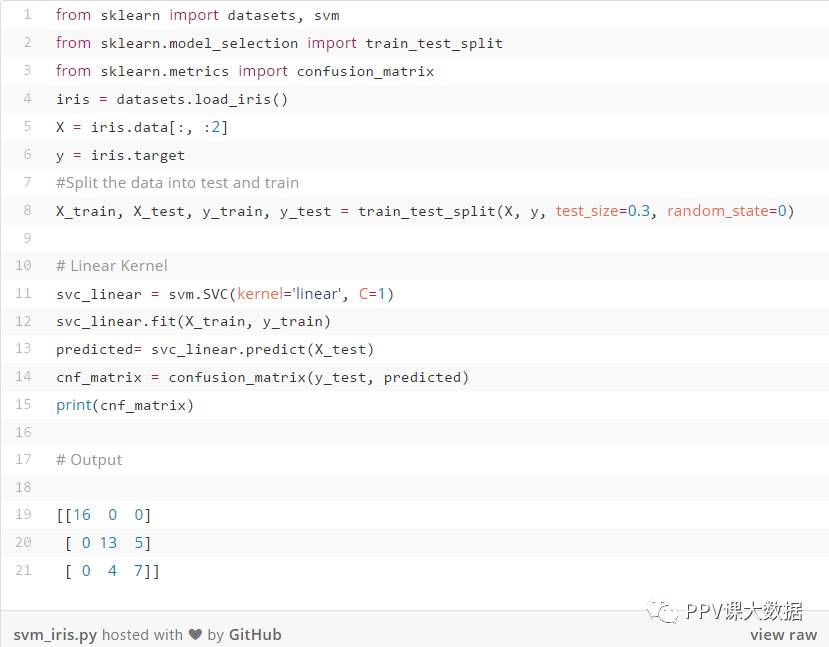
还可以通过更改参数和内核函数来调整SVM。 调整scikit-learn中可用参数的函数为gridSearchCV()。
sklearn.model_selection.GridSearchCV(estimator,param_grid)
此函数的参数定义如下:
estimator:它是估计器对象,在我们的例子中是svm.SVC()。
param_grid:它是具有参数名称(字符串)作为键的字典或列表,以及尝试作为值的参数设置列表。
想要了解更多关于GridSearch.CV()的其他参数,请点击这里(http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#)。
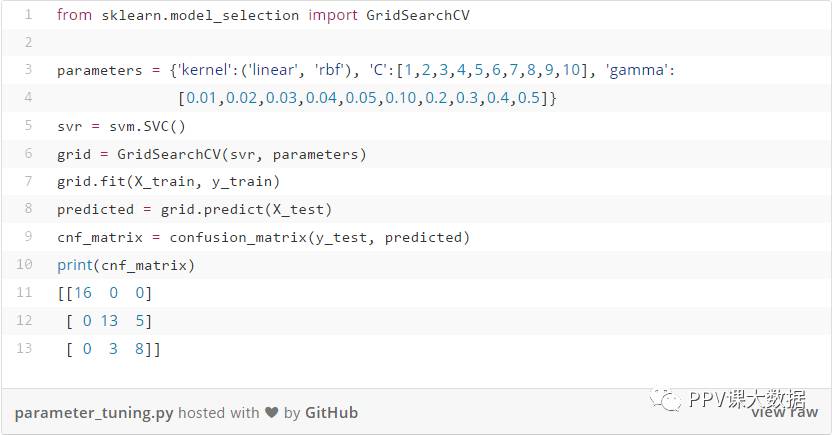
在上面的代码中,我们考虑调整的是核函数的参数,C和gamma。 从中得到最佳值的值是写在括号中的值。这里,我们只给出了几个值,也可以给出整个范围的值,但是它需要更长的执行时间。
R实现
我们在R中实现SVM算法的包是e1071。使用的函数是svm()。
总结
在本文中,我给出了SVM分类算法的非常基本的解释。我已经省略了一些复杂的数学问题,如计算距离和解决优化问题。但我希望通过这篇文章,你能了解一个机器学习算法SVM是如何基于已有的数据集建立起来的。
PPV课小组翻译 译:恬甜淡淡 转载请联系授权
以上是关于什么是调整后的R方的主要内容,如果未能解决你的问题,请参考以下文章
R语言计算调整的R方( Adjusted R-Squared)实战
R语言mgcv包中的gam函数拟合广义加性模型(Generalized Additive Model)GAM(对非线性变量进行样条处理计算RMSER方调整R方可视化模型预测值与真实值的曲线)
析因设计的方差分析的SPSS结果下有R方和调整R方值怎么解释
