析因设计的方差分析的SPSS结果下有R方和调整R方值怎么解释

Posted 2023-04-13

图片错了，是这张

这最下面的R squared 怎么解释

R方和 校正的R方 是为了说明 你的自变量A、自变量B以及A和B的交互作用，这三者一共可以解释多少因变量的方差变异。所以说跟回归的R方和调整的R方是一样的。可以说你的三个自变量解释因变量的64.5%的方差变异。

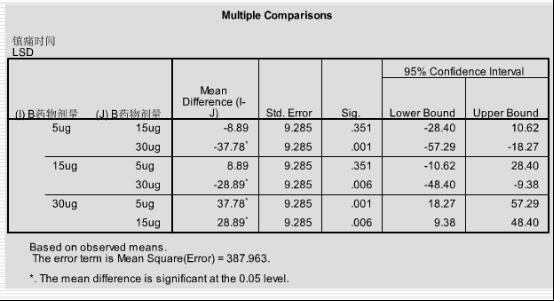
校正的R方比R方更加严谨一些。 参考技术A R2其实是回归模型的，决定系数 参考技术B 矫正了总变异追问

能说的更详细点吗

追答

不考虑常数intercept的变异

追问

这里的R square是回归模型里的决定系数吗，R square=0.755 数值有什么具体意义吗
我实在是不太懂，sorry

R语言单因素、多因素方差分析ANOVA analysis of variance

参考技术A

@[toc]

假设检验的前提是要满足正态分布和方差齐性

组内平方和SSE：同一组内的数据误差平方和
组间平方和SSA：不同组之间的数据误差平方和

一个分类型自变量
例如四个班级学生的语文成绩，班级是分类型自变量，四个班级是自变量的四个水平

测试班级对成绩的影响

因为p<0.001，说明班级对成绩的影响非常显著

图中跨越0分界线的班级对，有较大可能落在0上，也就是说两个班级之间没有明显差异。其他班级说明都有明显差异。

同一班级在大学三年的三次测试

p<0.001，说明学生成绩在大学三年中有显著差异。球形检验的p-value大于0.05，所以可以认为方差相等。

Mauchly\'s Test for Sphericity ：适用于重复测量时检验不同测量之间的差值的方差是否相等，用于三次以及三次之上。

Sphericity Corrections ：球形矫正，当方差不相等时进行矫正，矫正方法有the Greenhouse-Geisser (1959), the Huynh-Feldt (1976), 简称GG和HF。

两个分类型自变量
例如探究 词汇量 和 话题熟悉度 对学生作文成绩的影响

词汇量和话题熟悉度两个变量对成绩的影响都很显著，交互项对成绩影响不显著。

探究班级和测试次数对学生成绩的影响

班级和测试次数在原始检验中都很显著，然后交叉项不显著。

但是在球形检验中，推翻了方差齐性的假设，所以tests需要使用球形矫正之后的p值，classes不用。

矫正之前tests的p-value = 3.482406e-04，矫正之后的p-value = 0.001左右。