Python与矩阵论——特征值与特征向量

Posted 2020-12-03 既生喻何生亮(Bright)

Python计算特征值与特征向量案例

例子1

import numpy as np
A = np.array([[3,-1],[-1,3]])
print(\'打印A：\\n{}\'.format(A))
a, b = np.linalg.eig(A)
print(\'打印特征值a：\\n{}\'.format(a))
print(\'打印特征向量b：\\n{}\'.format(b))

打印A：
[[ 3 -1]
 [-1  3]]
打印特征值a：
[4. 2.]
打印特征向量b：
[[ 0.70710678  0.70710678]
 [-0.70710678  0.70710678]]

例子2

import numpy as np
A = np.array([[-1,1,0],[-4,3,0],[1,0,2]])
print(\'打印A：\\n{}\'.format(A))
a, b = np.linalg.eig(A)
print(\'打印特征值a：\\n{}\'.format(a))
print(\'打印特征向量b：\\n{}\'.format(b))

打印A：
[[-1  1  0]
 [-4  3  0]
 [ 1  0  2]]
打印特征值a：
[2. 1. 1.]
打印特征向量b：
[[ 0.          0.40824829  0.40824829]
 [ 0.          0.81649658  0.81649658]
 [ 1.         -0.40824829 -0.40824829]]

例子3

import numpy as np
A = np.array([[-2,1,1],[0,2,0],[-4,1,3]])
print(\'打印A：\\n{}\'.format(A))
a, b = np.linalg.eig(A)
print(\'打印特征值a：\\n{}\'.format(a))
print(\'打印特征向量b：\\n{}\'.format(b))

打印A：
[[-2  1  1]
 [ 0  2  0]
 [-4  1  3]]
打印特征值a：
[-1.  2.  2.]
打印特征向量b：
[[-0.70710678 -0.24253563  0.30151134]
 [ 0.          0.          0.90453403]
 [-0.70710678 -0.9701425   0.30151134]]

特征值

知识点：【奇异矩阵】

• 判断矩阵是不是方阵（即行数和列数相等的矩阵。若行数和列数不相等，那就谈不上奇异矩阵和非奇异矩阵）。 
• 看矩阵的行列式|A|是否等于0，若等于0，称矩阵A为奇异矩阵；若不等于0，称矩阵A为非奇异矩阵。

1. 若|A|≠0可知矩阵A可逆，可逆矩阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。　
2. 若A为奇异矩阵，则AX=0有无穷解，AX=b有无穷解或者无解。
3. 若A为非奇异矩阵，则AX=0有且只有唯一零解，AX=b有唯一解。

特征向量

总结：

特征值和特征向量的计算方法：

特征值与特征向量

特征值的性质：

特征向量的性质

 

例题1

 

import numpy as np
A = np.array([[1,2,2],[2,1,2],[2,2,1]])
print(\'打印A：\\n{}\'.format(A))
a, b = np.linalg.eig(A)
print(\'打印特征值a：\\n{}\'.format(a))
print(\'打印特征向量b：\\n{}\'.format(b))

打印A：
[[1 2 2]
 [2 1 2]
 [2 2 1]]
打印特征值a：
[-1.  5. -1.]
打印特征向量b：
[[-0.81649658  0.57735027  0.        ]
 [ 0.40824829  0.57735027 -0.70710678]
 [ 0.40824829  0.57735027  0.70710678]]

例题2

import numpy as np
A = np.array([[2,-3,1],[1,-2,1],[1,-3,2]])
print(\'打印A：\\n{}\'.format(A))
a, b = np.linalg.eig(A)
print(\'打印特征值a：\\n{}\'.format(a))
print(\'打印特征向量b：\\n{}\'.format(b))

打印A：
[[ 2 -3  1]
 [ 1 -2  1]
 [ 1 -3  2]]
打印特征值a：
[2.09037533e-15+0.00000000e+00j 1.00000000e+00+5.87474805e-16j
 1.00000000e+00-5.87474805e-16j]
打印特征向量b：
[[0.57735027+0.j         0.84946664+0.j         0.84946664-0.j        ]
 [0.57735027+0.j         0.34188085-0.11423045j 0.34188085+0.11423045j]
 [0.57735027+0.j         0.17617591-0.34269135j 0.17617591+0.34269135j]]

例题3

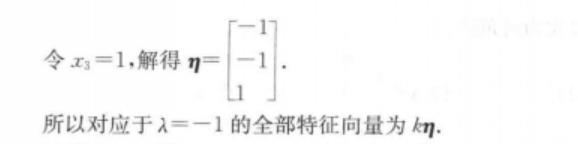
import numpy as np
A = np.array([[2,-1,2],[5,-3,3],[-1,0,-2]])
print(\'打印A：\\n{}\'.format(A))
a, b = np.linalg.eig(A)
print(\'打印特征值a：\\n{}\'.format(a))
print(\'打印特征向量b：\\n{}\'.format(b))

打印A：
[[ 2 -1  2]
 [ 5 -3  3]
 [-1  0 -2]]
打印特征值a：
[-0.99998465+0.00000000e+00j -1.00000768+1.32949166e-05j
 -1.00000768-1.32949166e-05j]
打印特征向量b：
[[ 0.57735027+0.00000000e+00j  0.57735027+7.67588259e-06j
   0.57735027-7.67588259e-06j]
 [ 0.57735913+0.00000000e+00j  0.57734584+1.53518830e-05j
   0.57734584-1.53518830e-05j]
 [-0.57734141+0.00000000e+00j -0.5773547 +0.00000000e+00j
  -0.5773547 -0.00000000e+00j]]