组合计数
Posted 邪童的博客
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了组合计数相关的知识,希望对你有一定的参考价值。
组合数
\\(C^m_n\\) = \\(\\dfracn (n-1) (n-2) \\cdots (n-m+1)m!\\) = \\(\\dfracn!m! (n-m)!\\)
\\(C^m_n\\) = \\(C^m_n-1\\) +\\(C^m-1_n-1\\)
递推法求组合数
求组合数Ⅰ \\(\\quad\\) \\(C^m_n\\) = \\(C^m_n-1\\) +\\(C^m-1_n-1\\)
//递推法求组合数模板
//c[a][b]存储C^a_b的方案数
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++)
if(j==0)c[i][j]=1;
else c[i][j]=c[i-1][j]+c[i-1][j-1];
预处理逆元求组合数
首先预处理出所有阶乘取模的余数 fact[N] , 以及所有阶乘取模的逆元 infact[N]
如果取模的数是质数, 可以用费马小定理求逆元
求组合数Ⅱ \\(\\quad\\) \\(C^m_n\\) = \\(\\dfracn!m!(n-m)!\\)
//快速幂模板
int qmi(int a,int k,int p)
int res=1;
while(k)
if(k&1)res=(long long)res*a%p;
a=a*a%p;
k>>=1;
return res;
//预处理阶乘的余数和阶乘余数的逆元
fact[0]=infact[0]=1;
for(int i=1;i<N;i++)
fact[i]=(long long)fact[i-1]*i%mod;
infact[i]=(long long)infact[i-1]*qmi(i,mod-2,mod)%mod;
Lucas定理
Lucas定理: 若p是质数, 则对于任意整数 1 \\(\\le\\) m \\(\\le\\) n , 有:
\\(C^m_n\\) \\(\\equiv\\) \\(C^m\\%p_n\\%p\\) \\(\\cdot\\) \\(C^m/p_n/p\\) (mod p)
求组合数Ⅲ \\(\\quad\\) \\(C^m_n\\) \\(\\equiv\\) \\(C^m\\%p_n\\%p\\) \\(\\cdot\\) \\(C^m/p_n/p\\) (mod p)
//快速幂模板
int qmi(int a,int k,int p)
int res=1;
while(k)
if(k&1)(long long)res=res*a%p;
a=(long long)a*a%p;
k>>=1;
return res;
//通过定理求组合数C^a_b
int C(int a,int b,int p)
if(a<b)return 0;
long long x=1,y=1; //x是分子,y是分母
for(int i=a,j=1;j<=b;i--,j++)
x=(long long)x*i%p;
y=(long long)y*j%p;
return x*(long long)qmi(y,p-2,p)%p;
int Lucas(long long a,long long b,int p)
if(a<p&&b<p)return C(a,b,p);
return (long long)C(a%p,b%p,p)*Lucas(a/p,b/p,p)%p;
分解质因数法求组合数
当我们需要求出组合数的真实值, 而非对某个数的余数时, 分解质因数的方式比较好用:
① 筛法求出范围内的所有质数
② 通过 \\(C^b_a\\) = \\(\\dfraca!b!(a-b)!\\) 这个公式求出每个质因子的次数
\\(\\quad\\) n ! 中 p 的次数是 [ \\(\\dfracnp\\) ] + [ \\(\\dfracnp^2\\) ] + \\(\\cdots\\)
③ 用高精度乘法将所有质因子相乘
int primes[N],cnt; //存储所有质数
int sum[N]; //存储每个质数的次数
bool st[N]; //存储每个数是否已被筛掉
void get_primes(int n) //线性筛法求素数
for(int i=2;i<=n;i++)
if(!st[i])primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
int get(int n,int p) //求n!中p的次数
int res=0;
while(n)
res+=n/p;
n/=p;
return res;
vector<int> mul (vector<int>a, int b) //高精度乘低精度模板
vector<int>c;
int t=0;
for(int i=0;i<a.size();i++)
t+=a[i]*b;
c.push_back(t%10);
t/=10;
while(t)
c.push_back(t%10);
t/=10;
return c;
get_primes(a); //预处理范围内的所有质数
for(int i=0;i<cnt;i++) //求每个质因数的次数
int p=primes[i];
sum[i]=get(a,p)-get(b,p)-get(a-b,p);
vector<int>res;
res.push_back(1);
for(int i=0;i<cnt;i++) //用高精度乘法将所有质因子相乘
for(int j=0;j<sum[i];j++)
res=mul(res,primes[i]);
卡特兰数
给定n个0和n个1, 它们按照某种顺序排成长度为2n的序列, 满足任意前缀中0的个数都不少于1的个数的序列的数量为:
Cat (n) = \\(C^n_2n\\) - \\(C^n-1_2n\\) = \\(\\dfracC^n_2nn+1\\)
组合数学 05 - 经典计数方法
1. 基本计数的母函数
现在来用母函数来求解基本计数问题,母函数既可以完成自动计数,还能表示计数本身,像Stirling数这种就只能用母函数表示。自动计数适用于可以分步的计数问题,并且目标值是每步值之和,这与多项式的运算性质有关。
1.1 组合数和分划数
直观上最符合这一特点的就是模型2,从\\(n\\)个可区别对象中选出\\(m个\\)。限制第\\(k\\)个对象被取的次数在集合\\(M_k\\)中,它被选情况的母函数是\\(\\sum\\limits_{i\\in M_k}x^i\\),所有元素被选择的情况可以借助母函数(1)自动计数,共选取\\(m\\)个元素的个数是\\(x^m\\)的系数。特别地,不可重复组合数的母函数是\\((1+x)^n\\),可重复组合数的母函数是\\(\\dfrac{1}{(1-x)^n}\\)(注意\\(1+x+x^2+\\cdots=\\dfrac{1}{1-x}\\)),满射的母函数是\\(\\dfrac{x^n}{(1-x)^n}\\)。
\\[\\sum_{k=0}^{\\infty}c_kx^k=\\prod_{i=1}^n\\left(\\sum_{j\\in M_i}x^j\\right)\\tag{1}\\]
对于模型4的分拆数,考虑到\\(1^{\\lambda_1}2^{\\lambda_2}\\cdots m^{\\lambda_m}\\)型分拆要满足上篇式(14),它也可以用母函数自动计数。对长度为\\(k\\)的分部使用\\(x^{k\\lambda_k}\\),故长度为\\(k\\)的分部的母函数是\\(1+x^k+x^{2k}+\\cdots=\\dfrac{1}{1-x^k}\\)。所以\\(p(m)\\)的母函数便是式(2),由于\\(p(m,k)\\)等于最大分部为\\(k\\)的分拆数,故它的母函数是式(3)。
\\[\\sum_{n=0}^{\\infty}p(n)x^n=\\prod_{i=1}^{\\infty}(1-x^i)^{-1}\\tag{2}\\]
\\[\\sum_{n=0}^{\\infty}p(n,k)x^n=x^k\\prod_{i=1}^k(1-x^i)^{-1}\\tag{3}\\]
值得一提的是,欧拉当初就是在研究分划数时发现母函数方法的。即使有式(2),\\(p(m)\\)的性质还是不清楚,我们注意到(2)的逆\\(q(x)\\)相对比较简单,值得讨论一下。\\(q(x)\\)有一个还算显然的组合意义,每一项系数的绝对值是分部互异的分划数,符号的意义则是分部数为奇数和偶数时分划数的差。利用这一组合意义辅助讨论(过程见教材),不难得到\\(q(m)\\)满足式(4)。继而可得到\\(p(m)\\)的递推关系式(5),它被称为欧拉公式。
\\[q(m)=\\left\\{\\begin{matrix}(-1)^k,&\\text{if}\\;m=\\frac{1}{2}(3k^2\\pm k)\\\\0,&\\text{if}\\;m\\ne\\frac{1}{2}(3k^2\\pm k)\\end{matrix}\\right.\\tag{4}\\]
\\[p(m)=\\sum_{k=1}^{\\infty}(-1)^{k-1}\\left(p(m-\\frac{3k^2-k}{2})+p(m-\\frac{3k^2+k}{2})\\right)\\tag{5}\\]
• 利用母函数证明:分部都为奇数的分划数等于分部互异的分划数。
1.2 指数型母函数
对于模型1的排列数,简单的相加显然不再满足,考察上篇式(2),这就启发我们用\\(\\dfrac{x^k}{k!}\\)代替\\(x^k\\)(式(6))。对于数列\\(c_n\\),级数(6)被称为数列的指数型母函数,它对排列问题非常适用。同上面的分析,\\(n\\)个互异元素中选\\(m\\)个排列的母函数是式(7)。特别地,无重复排列数的母函数是\\((1+x)^n\\),可重复排列数的母函数是\\(e^{nx}\\)(注意\\(1+x+\\dfrac{x^2}{2!}+\\cdots=e^x\\)),满射排列数的母函数则是\\((e^x-1)^n\\)。
\\[\\sum_{k=0}^{\\infty}c_k\\dfrac{x^k}{k!}=c_0+c_1\\dfrac{x}{1!}+c_2\\dfrac{x^2}{2!}+c_3\\dfrac{x^3}{3!}\\cdots\\tag{6}\\]
\\[\\sum_{k=0}^{\\infty}c_k\\dfrac{x^k}{k!}=\\prod_{i=1}^n\\left(\\sum_{j\\in M_i}\\dfrac{x^j}{j!}\\right)\\tag{7}\\]
最后趁热看一下模型3中的Stirling数,由于\\(k!S(m,k)\\)就是模型1中的满射,利用满射排列数的母函数容易知\\(S(m,k)\\)的指数型母函数(式(8)),利用指数型母函数也可以得到上篇式(26)。为了得到\\(s(m,k)\\)的指数型母函数\\(g_k(x)\\),从上篇式(27)右得到启发,先计算\\(g_k(x)\\)的母函数得到\\((1+x)^y\\)(过程略,二层母函数使用\\(y\\)),展开\\(y\\)的幂级数便得到\\(s(m,k)\\)的指数型母函数(9)。有了指数型母函数,Stirling数的性质就可以通过母函数研究,比如对母函数求导能得到递推关系式(10)(11)。
\\[\\sum_{m=0}^{\\infty}S(m,k)\\dfrac{x^m}{m!}=\\dfrac{1}{k!}(e^x-1)^k\\tag{8}\\]
\\[\\sum_{m=0}^{\\infty}s(m,k)\\dfrac{x^m}{m!}=\\dfrac{1}{k!}(\\ln(1-x))^k\\tag{9}\\]
\\[S(m,k)=\\sum_{i=k-1}^{m-1} \\binom{m-1}{i}S(i,k-1)\\tag{10}\\]
\\[s(m,k)=\\sum_{i=k-1}^{m-1}(-1)^{m-i-1}(m-1)_{m-i-1}s(i,k-1)\\tag{11}\\]
• 求每个元素取到偶数个的排列数。
2. Pólya计数定理
2.1 引言和环状字
基本计数问题中只涉及了两个最极端的拓扑结构,但在阐述的过程中,我们一直强调了同构类的思想。这里将推广这个思想,并将其用到更多的拓扑结构中。所谓同构,就是将拓扑结构中的元素置换,元素间的关系和置换后一致,它的代数意义就是我们熟悉的\\((a,b)=(f(a),g(a))\\)。我们这里就不再说元素可区分、不可区分了,每个元素单独看都无差别,它的差异性完全由其在拓扑结构中的位置决定。
比如图中的环状拓扑,直觉上说每个元素是“不可区分”的,但它们却不能随便置换。当把\\(a\\)置换到\\(a\'\\)时,为了保持\\(a,b\\)的关系,\\(b\\)只能置换到\\(b\'\\),所以这个拓扑中的同构就只能是整个图的旋转。再来看另一个环状拓扑,它除了旋转之外,延虚线的翻转也是同构置换。最后的立方体,其中包括更多同构置换,它们都与我们的直觉对应,就是变动后仍与以前一样。为了简单起见,以下我们只讨论原像是复杂拓扑,而像是可区分集的问题。它的等价模型就是给拓扑结构的元素染色,这时的同构当然还要求元素被置换到同样颜色的元素。
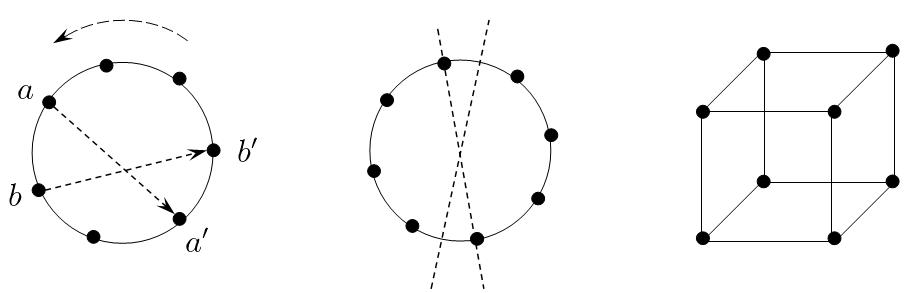
如果原像是左图的\\(m\\)阶有向环形,用\\(n\\)种颜色为其染色(或写入\\(n\\)种字母),结果被称为\\(m\\)元环状字,同构环状字的个数记作\\(C_n(m)\\)。先将环形固定并对其染色,将环状字进行旋转,得到的不同染色方案便是该染色同构的个数。如果颜色出现的最小周期为\\(d\\),易知共可以得到\\(d\\)个不同的染色,则有\\(n^m=\\sum\\limits_{d|m}dM(d)\\),其中\\(M(d)\\)是最小周期为\\(d\\)染色数(同构意义下)。利用反演公式可以得到\\(mM(m)=\\sum\\limits_{d|m}\\mu(\\dfrac{m}{d})n^d\\),从而有环状字的计数公式(12)。
\\[C_n(m)=\\sum_{d|m}\\sum_{d\'|d}\\mu(\\dfrac{d}{d\'})\\dfrac{n^{d\'}}{d}\\tag{12}\\]
2.2 Pólya计数定理
现在对问题做一般性的讨论,先假设原像是可区分的,在其上进行染色,得到了染色方案集\\(X\\)。还有对原像拓扑(不含颜色)进行同构置换的变换集\\(G\\),对任意\\(g\\in G\\),它都是一个变换\\(g:X\\to X\\)。当对\\(x_1,x_2\\in X\\),当存在\\(g\\in G\\)使得\\(g(x_1)=x_2\\)时,称\\(x_1,x_2\\)是等价的,而我们的问题就是求等价类的个数。
容易证明对每个拓扑结构,其所有的同构置换在复合运算下是封闭的,从而构成一个群。又由于它是置换群的子集,故也称对称群。\\(G\\)对\\(X\\)的变换满足条件(13),该变换是\\(G\\)在\\(X\\)上的“作用”,你需要先回顾一下“群的作用”相关知识。从两个维度分别讨论\\(g(x)=x\\),可以得到等价类的个数\\(N(G)\\)满足式(14)的Burnside定理,其中\\(F_g\\)表示满足\\(g(x)=x\\)的\\(x\\)的个数。如果对每个\\(x\\in X\\)加权\\(w(x)\\),并使得同一等价类中的元素权值相同,则有Burnside定理的加权版(式(15)),其中\\(x_k\\)是第\\(k\\)的等价类的代表元。
\\[(g_1g_2)(x)=g_1(g_2(x));\\;\\;e(x)=x\\tag{13}\\]
\\[N(G)=\\dfrac{1}{|G|}\\sum_{g\\in G}|F_g|\\tag{14}\\]
\\[\\sum_{k=1}^{N(G)}w(x_k)=\\dfrac{1}{|G|}\\sum_{g\\in G}(\\sum_{x\\in F_g}w(x))\\tag{15}\\]
在染色问题中,我们比较关心一个染色方案使用的颜色组合,为了体现这个信息,给每个颜色赋上权值\\(y_i\\)。而一个染色方案的权值则是\\(y_1^{k_1}y_2^{k_2}\\cdots y_n^{k_n}\\),其中\\(k_i\\)是颜色\\(i\\)出现的次数,且有\\(k_1+k_2+\\cdots+k_n=m\\)。式(15)包含了所有染色方案(同构意义下)的权值,其中我们可以得到每种颜色组合\\(k_1,k_2,\\cdots,k_n\\)下染色方案的个数。当然式(15)的计算是通过右边的式子得到的,右边聚焦于每一个置换\\(g\\)本身的性质,使得问题只与拓扑结构有关。
我们知道每个置换\\(g\\)其实是一些轮换的组合,比较显然(也很关键),\\(g(x)=x\\)的充要条件是同一轮换中的颜色相同。这里借用母函数的思想来计算\\(F_g\\)的权重,对长度为\\(k\\)的轮换,所有可能的权重之和是\\(y_1^k+y_2^k+\\cdots+y_n^k\\)。从而对\\(1^{\\lambda_1}2^{\\lambda_2}\\cdots m^{\\lambda_m}\\)型置换\\(g\\)的,\\(F_g\\)的权重如式(16)。为了表述方便,把式(17)称为\\(G\\)的轮换指标(cycle index),显然当\\(\\delta_k=y_1^k+y_2^k+\\cdots+y_n^k\\)时便得到权重的完整表达式,它也被称为式样清单。特别地,取\\(y_1=y_2=\\cdots=y_n=1\\)(即\\(\\delta_1=\\delta_2=\\cdots=\\delta_m=n\\)),便得到所有式样的个数(染色数)\\(P_G(n,\\cdots,n)\\),这些结论就是波利亚(Pálya)计数定理。
\\[w(F_g)=\\prod_{k=1}^n(y_1^k+y_2^k+\\cdots+y_n^k)^{\\lambda_k}\\tag{16}\\]
\\[P_G(\\sigma_1,\\cdots,\\sigma_m)=\\dfrac{1}{|G|}\\sum_{g\\in G}\\sigma_1^{\\lambda_1(g)}\\cdots\\sigma_m^{\\lambda_m(g)}\\tag{17}\\]
2.3 典型例子
波利亚定理采用了类似母函数的思想,能够准确地完成自动计数,但结论并没有给出最终计数值,所以它更多的在于其理论价值。下面以图中三种拓扑结构为例,阐述波利亚定理的应用,而问题的关键其实就是式(17)的计算。
首先是有向环,显然它的对称子群是一个\\(m\\)阶循环群\\(C_m=\\{g,g^2,\\cdots,g^m=e\\}\\),其中\\(g\\)是单步旋转。容易知道,\\(g^k\\)是\\((k,m)\\)个\\(\\dfrac{m}{(k,m)}\\)阶轮换之积,其中\\((k,m)\\)是最大公约数的记号。反过来考虑,对任意\\(d|m\\),有\\(\\varphi(\\dfrac{m}{d})\\)个\\(g^k\\)的轮换指标是\\(\\sigma_{m/d}^d\\)。所以其轮换指标是式(18),进而得到环状字的个数式(19),它和式(12)其实是等价的(\\(\\varphi(m)=\\sum\\limits_{d|m}\\mu(d)\\frac{m}{d}\\))。
\\[P_{C_m}=\\dfrac{1}{m}\\sum_{d|m}\\varphi(\\dfrac{m}{d})\\sigma_{m/d}^d=\\dfrac{1}{m}\\sum_{d|m}\\varphi(d)\\sigma_d^{m/d}\\tag{18}\\]
\\[C_n(m)=\\dfrac{1}{m}\\sum_{d|m}\\varphi(d)n^{\\frac{m}{d}}\\tag{19}\\]
再来看无向环,一个典型问题就是用不同颜色的珍珠能串成多少个不同的项链。它和有向环不同的是还可以进行翻转,它的对称子群\\(D_m=\\{g,g^2,\\cdots,g^m=e,ag,ag^2,\\cdots,ag^m=a\\}\\)被称为二面体群。其中后\\(m\\)个是翻转变换,当\\(m\\)是奇数时是\\(\\dfrac{n-1}{2}\\)个对换,当\\(n\\)为偶数时,一半是\\(\\dfrac{n}{2}\\)个对换,一半是\\(\\dfrac{n-2}{2}\\)个对换,翻转的轮换指标如式(20)。
\\[\\sum_{k=1}^mw(ag^k)=\\left\\{\\begin{matrix}\\dfrac{1}{2}x_1x_2^{\\frac{m-1}{2}},\\;\\;\\;\\;\\;\\;\\;\\;\\;\\;\\;&\\text{if m is odd}\\\\\\\\\\dfrac{1}{4}(x_2^{\\frac{m}{2}}+x_1^2x_2^{\\frac{m-2}{2}}),&\\text{if m is even}\\end{matrix}\\right.\\tag{20}\\]
最后来看立方体,立方体的对称群被称为立方体的旋转群,除了单位元外,还有以下三类旋转:(1)3*3=9个以对面中心为轴的旋转;(2)2*4=8个以过对顶点直线为轴的旋转;(4)1*6个以过对边中点直线为轴的旋转。这些变换可以分别作用在顶点、边和面上,其对应的轮换指标分别为如下三式所示。
\\[P_0=\\frac{1}{24}(x_1^8+9x_2^4+6x_4^2+8x_1^2x_3^2)\\;\\;\\;\\;\\;\\;\\tag{21}\\]
\\[P_1=\\frac{1}{24}(x_1^{12}+3x_2^6+6x_4^2+8x_3^4+6x_1^2x_2^5)\\;\\tag{22}\\]
\\[P_2=\\frac{1}{24}(x_1^6+3x_1^2x_2^2+6x_1^4x_4+6x_2^3+8x_3^2)\\tag{23}\\]
• 讨论\\(n\\)种颜色串成的项链种数,包括规定颜色数量的情况;
• 讨论\\(n\\)种颜色涂色立方体点、边、面的种数,包括规定颜色数量的情况。
以上是关于组合计数的主要内容,如果未能解决你的问题,请参考以下文章