组合数学 05 - 经典计数方法

Posted 2020-08-06 万物皆数

1. 基本计数的母函数

　　现在来用母函数来求解基本计数问题，母函数既可以完成自动计数，还能表示计数本身，像Stirling数这种就只能用母函数表示。自动计数适用于可以分步的计数问题，并且目标值是每步值之和，这与多项式的运算性质有关。

1.1 组合数和分划数

　　直观上最符合这一特点的就是模型2，从\\(n\\)个可区别对象中选出\\(m个\\)。限制第\\(k\\)个对象被取的次数在集合\\(M_k\\)中，它被选情况的母函数是\\(\\sum\\limits_{i\\in M_k}x^i\\)，所有元素被选择的情况可以借助母函数（1）自动计数，共选取\\(m\\)个元素的个数是\\(x^m\\)的系数。特别地，不可重复组合数的母函数是\\((1+x)^n\\)，可重复组合数的母函数是\\(\\dfrac{1}{(1-x)^n}\\)（注意\\(1+x+x^2+\\cdots=\\dfrac{1}{1-x}\\)），满射的母函数是\\(\\dfrac{x^n}{(1-x)^n}\\)。

\\[\\sum_{k=0}^{\\infty}c_kx^k=\\prod_{i=1}^n\\left(\\sum_{j\\in M_i}x^j\\right)\\tag{1}\\]

　　对于模型4的分拆数，考虑到\\(1^{\\lambda_1}2^{\\lambda_2}\\cdots m^{\\lambda_m}\\)型分拆要满足上篇式（14），它也可以用母函数自动计数。对长度为\\(k\\)的分部使用\\(x^{k\\lambda_k}\\)，故长度为\\(k\\)的分部的母函数是\\(1+x^k+x^{2k}+\\cdots=\\dfrac{1}{1-x^k}\\)。所以\\(p(m)\\)的母函数便是式（2），由于\\(p(m,k)\\)等于最大分部为\\(k\\)的分拆数，故它的母函数是式（3）。

\\[\\sum_{n=0}^{\\infty}p(n)x^n=\\prod_{i=1}^{\\infty}(1-x^i)^{-1}\\tag{2}\\]

\\[\\sum_{n=0}^{\\infty}p(n,k)x^n=x^k\\prod_{i=1}^k(1-x^i)^{-1}\\tag{3}\\]

　　值得一提的是，欧拉当初就是在研究分划数时发现母函数方法的。即使有式（2），\\(p(m)\\)的性质还是不清楚，我们注意到（2）的逆\\(q(x)\\)相对比较简单，值得讨论一下。\\(q(x)\\)有一个还算显然的组合意义，每一项系数的绝对值是分部互异的分划数，符号的意义则是分部数为奇数和偶数时分划数的差。利用这一组合意义辅助讨论（过程见教材），不难得到\\(q(m)\\)满足式（4）。继而可得到\\(p(m)\\)的递推关系式（5），它被称为欧拉公式。

\\[q(m)=\\left\\{\\begin{matrix}(-1)^k,&\\text{if}\\;m=\\frac{1}{2}(3k^2\\pm k)\\\\0,&\\text{if}\\;m\\ne\\frac{1}{2}(3k^2\\pm k)\\end{matrix}\\right.\\tag{4}\\]

\\[p(m)=\\sum_{k=1}^{\\infty}(-1)^{k-1}\\left(p(m-\\frac{3k^2-k}{2})+p(m-\\frac{3k^2+k}{2})\\right)\\tag{5}\\]

　　• 利用母函数证明：分部都为奇数的分划数等于分部互异的分划数。

1.2 指数型母函数

　　对于模型1的排列数，简单的相加显然不再满足，考察上篇式（2），这就启发我们用\\(\\dfrac{x^k}{k!}\\)代替\\(x^k\\)（式（6））。对于数列\\(c_n\\)，级数（6）被称为数列的指数型母函数，它对排列问题非常适用。同上面的分析，\\(n\\)个互异元素中选\\(m\\)个排列的母函数是式（7）。特别地，无重复排列数的母函数是\\((1+x)^n\\)，可重复排列数的母函数是\\(e^{nx}\\)（注意\\(1+x+\\dfrac{x^2}{2!}+\\cdots=e^x\\)），满射排列数的母函数则是\\((e^x-1)^n\\)。

\\[\\sum_{k=0}^{\\infty}c_k\\dfrac{x^k}{k!}=c_0+c_1\\dfrac{x}{1!}+c_2\\dfrac{x^2}{2!}+c_3\\dfrac{x^3}{3!}\\cdots\\tag{6}\\]

\\[\\sum_{k=0}^{\\infty}c_k\\dfrac{x^k}{k!}=\\prod_{i=1}^n\\left(\\sum_{j\\in M_i}\\dfrac{x^j}{j!}\\right)\\tag{7}\\]

　　最后趁热看一下模型3中的Stirling数，由于\\(k!S(m,k)\\)就是模型1中的满射，利用满射排列数的母函数容易知\\(S(m,k)\\)的指数型母函数（式（8）），利用指数型母函数也可以得到上篇式（26）。为了得到\\(s(m,k)\\)的指数型母函数\\(g_k(x)\\)，从上篇式（27）右得到启发，先计算\\(g_k(x)\\)的母函数得到\\((1+x)^y\\)（过程略，二层母函数使用\\(y\\)），展开\\(y\\)的幂级数便得到\\(s(m,k)\\)的指数型母函数（9）。有了指数型母函数，Stirling数的性质就可以通过母函数研究，比如对母函数求导能得到递推关系式（10）（11）。

\\[\\sum_{m=0}^{\\infty}S(m,k)\\dfrac{x^m}{m!}=\\dfrac{1}{k!}(e^x-1)^k\\tag{8}\\]

\\[\\sum_{m=0}^{\\infty}s(m,k)\\dfrac{x^m}{m!}=\\dfrac{1}{k!}(\\ln(1-x))^k\\tag{9}\\]

\\[S(m,k)=\\sum_{i=k-1}^{m-1} \\binom{m-1}{i}S(i,k-1)\\tag{10}\\]

\\[s(m,k)=\\sum_{i=k-1}^{m-1}(-1)^{m-i-1}(m-1)_{m-i-1}s(i,k-1)\\tag{11}\\]

　　• 求每个元素取到偶数个的排列数。

2. Pólya计数定理

2.1 引言和环状字

　　基本计数问题中只涉及了两个最极端的拓扑结构，但在阐述的过程中，我们一直强调了同构类的思想。这里将推广这个思想，并将其用到更多的拓扑结构中。所谓同构，就是将拓扑结构中的元素置换，元素间的关系和置换后一致，它的代数意义就是我们熟悉的\\((a,b)=(f(a),g(a))\\)。我们这里就不再说元素可区分、不可区分了，每个元素单独看都无差别，它的差异性完全由其在拓扑结构中的位置决定。

　　比如图中的环状拓扑，直觉上说每个元素是“不可区分”的，但它们却不能随便置换。当把\\(a\\)置换到\\(a\'\\)时，为了保持\\(a,b\\)的关系，\\(b\\)只能置换到\\(b\'\\)，所以这个拓扑中的同构就只能是整个图的旋转。再来看另一个环状拓扑，它除了旋转之外，延虚线的翻转也是同构置换。最后的立方体，其中包括更多同构置换，它们都与我们的直觉对应，就是变动后仍与以前一样。为了简单起见，以下我们只讨论原像是复杂拓扑，而像是可区分集的问题。它的等价模型就是给拓扑结构的元素染色，这时的同构当然还要求元素被置换到同样颜色的元素。

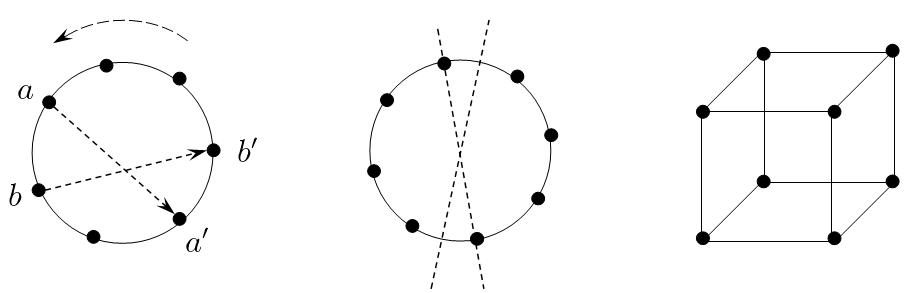
　　如果原像是左图的\\(m\\)阶有向环形，用\\(n\\)种颜色为其染色（或写入\\(n\\)种字母），结果被称为\\(m\\)元环状字，同构环状字的个数记作\\(C_n(m)\\)。先将环形固定并对其染色，将环状字进行旋转，得到的不同染色方案便是该染色同构的个数。如果颜色出现的最小周期为\\(d\\)，易知共可以得到\\(d\\)个不同的染色，则有\\(n^m=\\sum\\limits_{d|m}dM(d)\\)，其中\\(M(d)\\)是最小周期为\\(d\\)染色数（同构意义下）。利用反演公式可以得到\\(mM(m)=\\sum\\limits_{d|m}\\mu(\\dfrac{m}{d})n^d\\)，从而有环状字的计数公式（12）。

\\[C_n(m)=\\sum_{d|m}\\sum_{d\'|d}\\mu(\\dfrac{d}{d\'})\\dfrac{n^{d\'}}{d}\\tag{12}\\]

2.2 Pólya计数定理

　　现在对问题做一般性的讨论，先假设原像是可区分的，在其上进行染色，得到了染色方案集\\(X\\)。还有对原像拓扑（不含颜色）进行同构置换的变换集\\(G\\)，对任意\\(g\\in G\\)，它都是一个变换\\(g:X\\to X\\)。当对\\(x_1,x_2\\in X\\)，当存在\\(g\\in G\\)使得\\(g(x_1)=x_2\\)时，称\\(x_1,x_2\\)是等价的，而我们的问题就是求等价类的个数。

　　容易证明对每个拓扑结构，其所有的同构置换在复合运算下是封闭的，从而构成一个群。又由于它是置换群的子集，故也称对称群。\\(G\\)对\\(X\\)的变换满足条件（13），该变换是\\(G\\)在\\(X\\)上的“作用”，你需要先回顾一下“群的作用”相关知识。从两个维度分别讨论\\(g(x)=x\\)，可以得到等价类的个数\\(N(G)\\)满足式（14）的Burnside定理，其中\\(F_g\\)表示满足\\(g(x)=x\\)的\\(x\\)的个数。如果对每个\\(x\\in X\\)加权\\(w(x)\\)，并使得同一等价类中的元素权值相同，则有Burnside定理的加权版（式（15）），其中\\(x_k\\)是第\\(k\\)的等价类的代表元。

\\[(g_1g_2)(x)=g_1(g_2(x));\\;\\;e(x)=x\\tag{13}\\]

\\[N(G)=\\dfrac{1}{|G|}\\sum_{g\\in G}|F_g|\\tag{14}\\]

\\[\\sum_{k=1}^{N(G)}w(x_k)=\\dfrac{1}{|G|}\\sum_{g\\in G}(\\sum_{x\\in F_g}w(x))\\tag{15}\\]

　　在染色问题中，我们比较关心一个染色方案使用的颜色组合，为了体现这个信息，给每个颜色赋上权值\\(y_i\\)。而一个染色方案的权值则是\\(y_1^{k_1}y_2^{k_2}\\cdots y_n^{k_n}\\)，其中\\(k_i\\)是颜色\\(i\\)出现的次数，且有\\(k_1+k_2+\\cdots+k_n=m\\)。式（15）包含了所有染色方案（同构意义下）的权值，其中我们可以得到每种颜色组合\\(k_1,k_2,\\cdots,k_n\\)下染色方案的个数。当然式（15）的计算是通过右边的式子得到的，右边聚焦于每一个置换\\(g\\)本身的性质，使得问题只与拓扑结构有关。

　　我们知道每个置换\\(g\\)其实是一些轮换的组合，比较显然（也很关键），\\(g(x)=x\\)的充要条件是同一轮换中的颜色相同。这里借用母函数的思想来计算\\(F_g\\)的权重，对长度为\\(k\\)的轮换，所有可能的权重之和是\\(y_1^k+y_2^k+\\cdots+y_n^k\\)。从而对\\(1^{\\lambda_1}2^{\\lambda_2}\\cdots m^{\\lambda_m}\\)型置换\\(g\\)的，\\(F_g\\)的权重如式（16）。为了表述方便，把式（17）称为\\(G\\)的轮换指标（cycle index），显然当\\(\\delta_k=y_1^k+y_2^k+\\cdots+y_n^k\\)时便得到权重的完整表达式，它也被称为式样清单。特别地，取\\(y_1=y_2=\\cdots=y_n=1\\)（即\\(\\delta_1=\\delta_2=\\cdots=\\delta_m=n\\)），便得到所有式样的个数（染色数）\\(P_G(n,\\cdots,n)\\)，这些结论就是波利亚（Pálya）计数定理。

\\[w(F_g)=\\prod_{k=1}^n(y_1^k+y_2^k+\\cdots+y_n^k)^{\\lambda_k}\\tag{16}\\]

\\[P_G(\\sigma_1,\\cdots,\\sigma_m)=\\dfrac{1}{|G|}\\sum_{g\\in G}\\sigma_1^{\\lambda_1(g)}\\cdots\\sigma_m^{\\lambda_m(g)}\\tag{17}\\]

2.3 典型例子

　　波利亚定理采用了类似母函数的思想，能够准确地完成自动计数，但结论并没有给出最终计数值，所以它更多的在于其理论价值。下面以图中三种拓扑结构为例，阐述波利亚定理的应用，而问题的关键其实就是式（17）的计算。

　　首先是有向环，显然它的对称子群是一个\\(m\\)阶循环群\\(C_m=\\{g,g^2,\\cdots,g^m=e\\}\\)，其中\\(g\\)是单步旋转。容易知道，\\(g^k\\)是\\((k,m)\\)个\\(\\dfrac{m}{(k,m)}\\)阶轮换之积，其中\\((k,m)\\)是最大公约数的记号。反过来考虑，对任意\\(d|m\\)，有\\(\\varphi(\\dfrac{m}{d})\\)个\\(g^k\\)的轮换指标是\\(\\sigma_{m/d}^d\\)。所以其轮换指标是式（18），进而得到环状字的个数式（19），它和式（12）其实是等价的（\\(\\varphi(m)=\\sum\\limits_{d|m}\\mu(d)\\frac{m}{d}\\)）。

\\[P_{C_m}=\\dfrac{1}{m}\\sum_{d|m}\\varphi(\\dfrac{m}{d})\\sigma_{m/d}^d=\\dfrac{1}{m}\\sum_{d|m}\\varphi(d)\\sigma_d^{m/d}\\tag{18}\\]

\\[C_n(m)=\\dfrac{1}{m}\\sum_{d|m}\\varphi(d)n^{\\frac{m}{d}}\\tag{19}\\]

　　再来看无向环，一个典型问题就是用不同颜色的珍珠能串成多少个不同的项链。它和有向环不同的是还可以进行翻转，它的对称子群\\(D_m=\\{g,g^2,\\cdots,g^m=e,ag,ag^2,\\cdots,ag^m=a\\}\\)被称为二面体群。其中后\\(m\\)个是翻转变换，当\\(m\\)是奇数时是\\(\\dfrac{n-1}{2}\\)个对换，当\\(n\\)为偶数时，一半是\\(\\dfrac{n}{2}\\)个对换，一半是\\(\\dfrac{n-2}{2}\\)个对换，翻转的轮换指标如式（20）。

\\[\\sum_{k=1}^mw(ag^k)=\\left\\{\\begin{matrix}\\dfrac{1}{2}x_1x_2^{\\frac{m-1}{2}},\\;\\;\\;\\;\\;\\;\\;\\;\\;\\;\\;&\\text{if m is odd}\\\\\\\\\\dfrac{1}{4}(x_2^{\\frac{m}{2}}+x_1^2x_2^{\\frac{m-2}{2}}),&\\text{if m is even}\\end{matrix}\\right.\\tag{20}\\]

　　最后来看立方体，立方体的对称群被称为立方体的旋转群，除了单位元外，还有以下三类旋转：（1）3*3=9个以对面中心为轴的旋转；（2）2*4=8个以过对顶点直线为轴的旋转；（4）1*6个以过对边中点直线为轴的旋转。这些变换可以分别作用在顶点、边和面上，其对应的轮换指标分别为如下三式所示。

\\[P_0=\\frac{1}{24}(x_1^8+9x_2^4+6x_4^2+8x_1^2x_3^2)\\;\\;\\;\\;\\;\\;\\tag{21}\\]

\\[P_1=\\frac{1}{24}(x_1^{12}+3x_2^6+6x_4^2+8x_3^4+6x_1^2x_2^5)\\;\\tag{22}\\]

\\[P_2=\\frac{1}{24}(x_1^6+3x_1^2x_2^2+6x_1^4x_4+6x_2^3+8x_3^2)\\tag{23}\\]

　　• 讨论\\(n\\)种颜色串成的项链种数，包括规定颜色数量的情况；

　　• 讨论\\(n\\)种颜色涂色立方体点、边、面的种数，包括规定颜色数量的情况。