局部加权之逻辑回归 - Python实现
Posted LOGAN_XIONG
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了局部加权之逻辑回归 - Python实现相关的知识，希望对你有一定的参考价值。
- 算法特征:
利用sigmoid函数的概率含义, 借助回归之手段达到分类之目的. - 算法推导:
Part Ⅰ
sigmoid函数之定义:
\\begin{equation}\\label{eq_1}
sig(x) = \\frac{1}{1 + e^{-x}}
\\end{equation}
相关函数图像: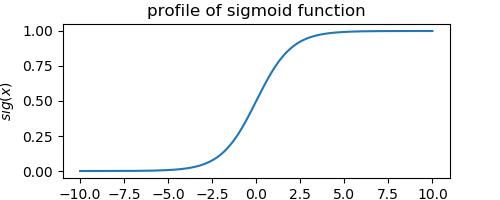
由此可见, sigmoid函数将整个实数域$(-\\infty, +\\infty)$映射至$(0, 1)$区间内, 反映了一种良好概率意义下的映射关系. 对该函数进行如下扩展:
\\begin{equation}\\label{eq_2}
sig(\\theta(x)) = \\frac{1}{1 + e^{-\\theta(x)}}
\\end{equation}
其中, $x$为输入参数, $\\theta(x)$为sigmoid函数之相位. 展开该相位, 可获取sigmoid函数之特征线$\\theta(x) = c$, 特征线$\\theta(x) = 0$也就是我们最常见的分界线. 很显然, 相位$\\theta(x)$之具体形式将影响分界线最终的表达能力, 即分界线形状的复杂程度.
为避免混淆, 现将相位$\\theta(x)$拆开:①. $x$ ~ 输入参数; ②. $\\theta$ ~ 相位参数. 在具有严格数理要求的情形下, 相位参数按实际要求选取; 否则, 经过训练集上的交叉验证选择合适的形式即可.
Part Ⅱ
现建立如下假设模型:
\\begin{equation}\\label{eq_4}
h_{\\theta}(x) = sig(\\theta(x))
\\end{equation}
以$y = 1$表示正例, $y = 0$表示负例. 令$h_{\\theta}(x)$表示输入参数$x$取正例之概率, $1 - h_{\\theta}(x)$表示输入参数$x$取负例之概率, 则假设模型对输入参数$x$预测正确之概率(正例情况下预测正例之概率、负例情况下预测负例之概率)为:
\\begin{equation}\\label{eq_5}
P(right \\mid x, \\theta) = h_{\\theta}(x)^y(1 - h_{\\theta}(x))^{(1 - y)}
\\end{equation}
考虑训练集中存在$n$个样本, 假设相位参数$\\theta$已知, 则此n个样本同时预测正确之概率为:
\\begin{equation}\\label{eq_6}
L(\\theta) = \\prod_{i = 1}^{n}P(right \\mid x^{(i)}, \\theta)
\\end{equation}
对该似然函数取对数似然:
\\begin{equation}\\label{eq_7}
lnL(\\theta) = \\sum_{i = 1}^{n}lnP(right \\mid x^{(i)}, \\theta)
\\end{equation}
定义损失函数:
\\begin{equation}\\label{eq_8}
J(\\theta) = -\\frac{1}{n}lnL(\\theta)
\\end{equation}
根据最大似然估计, 有如下无约束最优化问题:
\\begin{equation}\\label{eq_9}
min\\ J(\\theta)
\\end{equation}
其中, 相位参数$\\theta$为优化变量. 对该优化问题进行求解, 即可获取相位参数$\\theta$之最优解, 也即当前训练集下的最优分类模型.
Part Ⅲ
为方便优化, 给出如下协助信息:
\\begin{equation}\\label{eq_10}
\\left\\{\\begin{matrix}
\\nabla h_{\\theta} = h_{\\theta}(1 - h_{\\theta})\\nabla \\theta \\\\
\\nabla lnh_{\\theta} = (1 - h_{\\theta})\\nabla \\theta \\\\
\\nabla ln(1 - h_{\\theta}) = -h_{\\theta}\\nabla \\theta
\\end{matrix}\\right.
\\end{equation}
目标函数$J(\\theta)$之gradient:
\\begin{equation}\\label{eq_11}
\\nabla J = -\\frac{1}{n} \\sum_{i = 1}^{n} (y^{(i)} - h_{\\theta}(x^{(i)}))\\nabla \\theta \\\\
\\end{equation}
目标函数$J(\\theta)$之Hessian矩阵:
\\begin{equation}\\label{eq_12}
H = \\nabla^2 J = -\\frac{1}{n} \\sum_{i = 1}^{n}[(y^{(i)} - h_{\\theta}(x^{(i)}))\\nabla^2 \\theta - h_{\\theta}(x^{(i)})(1 - h_{\\theta}(x^{(i)}))\\nabla \\theta (\\nabla \\theta)^T]
\\end{equation}
Part Ⅳ
引入局部加权项$exp(-\\left \\| x_i - x\\right \\|_2^2 / (2\\tau^2))$, 引入原则:
①. 不改变损失函数$J(\\theta)$中各样本的损失贡献计算方式;
②. 对样本的损失贡献独立进行加权.
③. 泛化误差之计算仅依赖于样本的损失贡献.
Part Ⅴ
现以一个二分类为例进行算法实施.
以常见的$\\theta(x) = 0$作为分界线, 并令:
\\begin{equation}
\\left\\{\\begin{matrix}
h_{\\theta}(x) \\geq 0.5 & y = 1 & 正例 \\\\
h_{\\theta}(x) < 0.5 & y = 0 & 负例
\\end{matrix}\\right.
\\end{equation} - 代码实现:
笔者所用训练集与测试集数据分布如下:
View Code1 # 局部加权之逻辑回归 2 3 import numpy 4 from matplotlib import pyplot as plt 5 6 7 def spiral_point(val, center=(0.5, 0.5)): 8 rn = 0.4 * (105 - val) / 104 9 an = numpy.pi * (val - 1) / 25 10 11 x0 = center[0] + rn * numpy.sin(an) 12 y0 = center[1] + rn * numpy.cos(an) 13 z0 = 0 14 x1 = center[0] - rn * numpy.sin(an) 15 y1 = center[1] - rn * numpy.cos(an) 16 z1 = 1 17 18 return (x0, y0, z0), (x1, y1, z1) 19 20 21 def spiral_data(valList): 22 dataList = list(spiral_point(val) for val in valList) 23 data0 = numpy.array(list(item[0] for item in dataList)) 24 data1 = numpy.array(list(item[1] for item in dataList)) 25 return data0, data1 26 27 28 # 生成训练数据集 29 trainingValList = numpy.arange(1, 101, 1) 30 trainingData0, trainingData1 = spiral_data(trainingValList) 31 trainingSet = numpy.vstack((trainingData0, trainingData1)) 32 33 # 生成测试数据集 34 testValList = numpy.arange(1.5, 101.5, 1) 35 testData0, testData1 = spiral_data(testValList) 36 testSet = numpy.vstack((testData0, testData1)) 37 38 39 # 假设模型 40 def h_theta(x, theta): 41 val = 1. / (1. + numpy.exp(-numpy.sum(x * theta))) 42 return val 43 44 45 # 假设模型预测正确之概率 46 def p_right(x, y_, theta): 47 val = h_theta(x, theta) ** y_ * (1. - h_theta(x, theta)) ** (1 - y_) 48 return val 49 50 51 # 加权损失函数 52 def JW(X, Y_, W, theta): 53 JVal = 0 54 for colIdx in range(X.shape[1]): 55 x = X[:, colIdx:colIdx+1] 56 y_ = Y_[colIdx, 0] 57 w = W[colIdx, 0] 58 pVal = p_right(x, y_, theta) if p_right(x, y_, theta) >= 1.e-100 else 1.e-100 59 JVal += w * numpy.log(pVal) 60 JVal = -JVal / X.shape[1] 61 return JVal 62 63 64 # 加权损失函数之梯度 65 def JW_grad(X, Y_, W, theta): 66 grad = numpy.zeros(shape=theta.shape) 67 for colIdx in range(X.shape[1]): 68 x = X[:, colIdx:colIdx+1] 69 y_ = Y_[colIdx, 0] 70 w = W[colIdx, 0] 71 grad += w * (y_ - h_theta(x, theta)) * x 72 grad = -grad / X.shape[1] 73 return grad 74 75 76 # 加权损失函数之Hessian 77 def JW_Hess(X, Y_, W, theta): 78 Hess = numpy.zeros(shape=(theta.shape[0], theta.shape[0])) 79 for colIdx in range(X.shape[1]): 80 x = X[:, colIdx:colIdx+1] 81 y_ = Y_[colIdx, 0] 82 w = W[colIdx, 0] 83 Hess += w * h_theta(x, theta) * (1 - h_theta(x, theta)) * numpy.matmul(x, x.T) 84 Hess = Hess / X.shape[1] 85 return Hess 86 87 88 class LWLR(object): 89 90 def __init__(self, trainingSet, tauBound=(0.001, 0.1), epsilon=1.e-3): 91 self.__trainingSet = trainingSet # 训练集 92 self.__tauBound = tauBound # tau之搜索边界 93 self.__epsilon = epsilon # tau之搜索精度 94 95 96 def search_tau(self): 97 \'\'\' 98 交叉验证返回最优tau 99 采用黄金分割法计算最优tau 100 \'\'\' 101 X, Y_ = self.__get_XY_(self.__trainingSet) 102 lowerBound, upperBound = self.__tauBound 103 lowerTau = self.__calc_lowerTau(lowerBound, upperBound) 104 upperTau = self.__calc_upperTau(lowerBound, upperBound) 105 lowerErr = self.__calc_generalErr(X, Y_, lowerTau) 106 upperErr = self.__calc_generalErr(X, Y_, upperTau) 107 108 while (upperTau - lowerTau) > self.__epsilon: 109 if lowerErr > upperErr: 110 lowerBound = lowerTau 111 lowerTau = upperTau 112 lowerErr = upperErr 113 upperTau = self.__calc_upperTau(lowerBound, upperBound) 114 upperErr = self.__calc_generalErr(X, Y_, upperTau) 115 else: 116 upperBound = upperTau 117 upperTau = lowerTau 118 upperErr = lowerErr 119 lowerTau = self.__calc_lowerTau(lowerBound, upperBound) 120 lowerErr = self.__calc_generalErr(X, Y_, lowerTau) 121 # print("{}, {}~{}, {}~{}, {}".format(lowerBound, lowerTau, lowerErr, upperTau, upperErr, upperBound)) 122 self.bestTau = (upperTau + lowerTau) / 2 123 # print(self.bestTau) 124 return self.bestTau 125 126 127 def __calc_generalErr(self, X, Y_, tau): 128 cnt = 0 129 generalErr = 0 130 131 for idx in range(X.shape[1]): 132 tmpx = X[:, idx:idx+1] 133 tmpy_ = Y_[idx, 0] 134 tmpX = numpy.hstack((X[:, 0:idx], X[:, idx+1:])) 135 tmpY_ = numpy.vstack((Y_[0:idx, :], Y_[idx+1:, :])) 136 tmpW = self.__get_W(tmpx, tmpX, tau) 137 theta, tab = self.__optimize_theta(tmpX, tmpY_, tmpW) 138 # print(idx, tab, tmpx.reshape(-1), tmpy_, h_theta(tmpx, theta), theta.reshape(-1)) 139 if not tab: 140 continue 141 cnt += 1 142 generalErr -= numpy.log(p_right(tmpx, tmpy_, theta)) 143 generalErr /= cnt 144 # print(tau, generalErr) 145 return generalErr 146 147 148 def __calc_lowerTau(self, lowerBound, upperBound): 149 delta = upperBound - lowerBound 150 lowerTau = upperBound - delta * 0.618 151 return lowerTau 152 153 154 def __calc_upperTau(self, lowerBound, upperBound): 155 delta = upperBound - lowerBound 156 upperTau = lowerBound + delta * 0.618 157 return upperTau 158 159 160 def __optimize_theta(self, X, Y_, W, maxIter=1000, epsilon=1.e-9): 161 \'\'\' 162 maxIter: 最大迭代次数 163 epsilon: 收敛判据 ~ 梯度趋于0则收敛 164 \'\'\' 165 theta = self.__init_theta((X.shape[0], 1)) 166 JVal = JW(X, Y_, W, theta) 167 grad = JW_grad(X, Y_, W, theta) 168 Hess = JW_Hess(X, Y_, W, theta) 169 for i in range(maxIter): 170 if self.__is_converged1(grad, epsilon): 171 return theta, True 172 173 dCurr = -numpy.matmul(numpy.linalg.inv(Hess + 1.e-9 * numpy.identity(Hess.shape[0])), grad) 174 alpha = self.__calc_alpha_by_ArmijoRule(theta, JVal, grad, dCurr, X, Y_, W) 175 176 thetaNew = theta + alpha * dCurr 177 JValNew = JW(X, Y_, W, thetaNew) 178 if self.__is_converged2(thetaNew - theta, JValNew - JVal, epsilon): 179 return thetaNew, True 180 181 theta = thetaNew 182 JVal = JValNew 183 grad = JW_grad(X, Y_, W, theta) 184 Hess = JW_Hess(X, Y_, W, theta) 185 # print(i, JVal, grad.reshape(-1)) 186 else: 187 if self.__is_converged1(grad, epsilon): 188 return theta, True 189 190 return theta, False 191 192 193 def __calc_alpha_by_ArmijoRule(self, thetaCurr, JCurr, gCurr, dCurr, X, Y_, W, c=1.e-4, v=0.5): 194 i = 0 195 alpha = v ** i 196 thetaNext = thetaCurr + alpha * dCurr 197 JNext = JW(X, Y_, W, thetaNext) 198 while True: 199 if JNext <= JCurr + c * alpha * numpy.matmul(dCurr.T, gCurr)[0, 0]: break 200 i += 1 201 alpha = v ** i 202 thetaNext = thetaCurr + alpha * dCurr 203 JNext = JW(X, Y_, W, thetaNext) 204 205 return alpha 206 207 208 def __is_converged1(self, grad, epsilon): 209 if numpy.linalg.norm(grad) <= epsilon: 210 return True 211 return False 212 213 214 def __is_converged2(self, thetaDelta, JValDelta, epsilon): 215 if numpy.linalg.norm(thetaDelta) <= epsilon or numpy.linalg.norm(JValDelta) <= epsilon: 216 return True 217 return False 218 219 220 def __init_theta(self, shape): 221 \'\'\' 222 theta之初始化 223 \'\'\' 224 thetaInit = numpy.zeros(shape=shape) 225 return thetaInit 226 227 228 def __get_XY_(self, dataSet): 229 self.X = dataSet[:, 0:2].T # 注意数值溢出 230 self.X = numpy.vstack((self.X, numpy.ones(shape=(1, self.X.shape[1])))) 231 self.Y_ = dataSet[:, 2:3] 232 return self.X, self.Y_ 233 234 235 def __get_W(self, x, X, tau): 236 term1 = numpy.sum((X - x) ** 2, axis=0) 237 term2 = -term1 / (2 * tau ** 2) 238 term3 = numpy.exp(term2) 239 W = term3.reshape(-1, 1) 240 return W 241 242 243 def get_cls(self, x, tau=None, midVal=0.5): 244 if tau is None: 245 if not hasattr(self, "bestTau"): 246 self.search_tau() 247 tau = self.bestTau 248 if not hasattr(self, "X"): 249 self.__get_XY_(self.__trainingSet) 250 251 tmpx = numpy.vstack((numpy.array(x).reshape(-1, 1), numpy.ones(shape=(1, 1)))) # 注意数值溢出 252 tmpW = self.__get_W(tmpx, self.X, tau) 253 theta, tab = self.__optimize_theta(self.X, self.Y_, tmpW) 254 255 realVal = h_theta(tmpx, theta) 256 if realVal > midVal: # 正例 257 return 1 258 elif realVal == midVal: # 中间 259 return 0.5 260 else: # 负例 261 return 0 262 263 264 def get_accuracy(self, testSet, tau=None, midVal=0.5): 265 \'\'\' 266 正确率计算 267 \'\'\' 268 if tau is None: 269 if not hasattr(self, "bestTau"): 270 self.search_tau() 271 tau = self.bestTau 272 273 rightCnt = 0 274 for row in testSet: 275 cls = self.get_cls(row[:2], tau, midVal) 276 if cls == row[2]: 277 rightCnt += 1 278 279 accuracy = rightCnt / testSet.shape[0] 280 return accuracy 281 282 283 class SpiralPlot(object): 284 285 def spiral_data_plot(self, trainingData0, trainingData1, testData0, testData1): 286 fig = plt.figure(figsize=(5, 5)) 287 ax1 = plt.subplot() 288 ax1.scatter(trainingData1[:, 0], trainingData1[:, 1], c="red", marker="o", s=10, label="training data - Positive") 289 ax1.scatter(trainingData0[:, 0], trainingData0[:, 1], c="blue", marker="o", s=10, label="training data - Negative") 290 291 ax1.scatter(testData1[:, 0], testData1[:, 1], c="red", marker="x", s=10, label="test data - Positive") 292 ax1.scatter(testData0[:, 0], testData0[:, 1], c="blue", marker="x", s=10, label="test data - Negative") 293 ax1.set(xlim=(0, 1), ylim=(0, 1), xlabel="$x_1$", ylabel="$x_2$") 294 plt.legend(fontsize="x-small") 295 fig.tight_layout() 296 fig.savefig("spiral.png", dpi=100) 297 plt.close() 298 299 300 def spiral_pred_plot(self, lwlrObj, tau, trainingData0=trainingData0, trainingData1=trainingData1): 301 x = numpy.linspace(0, 1, 500) 302 y = numpy.linspace(0, 1, 500) 303 x, y = numpy.meshgrid(x, y) 304 z = numpy.zeros(shape=x.shape) 305 for rowIdx in range(x.shape[0]): 306 for colIdx in range(x.shape[1]): 307 z[rowIdx, colIdx] = lwlrObj.get_cls((x[rowIdx, colIdx], y[rowIdx, colIdx]), tau=tau) 308 # print(rowIdx) 309 # print(z) 310 cls2color = {0: "blue", 0.5: "white", 1: "red"} 311 312 fig = plt.figure(figsize=(5, 5)) 313 ax1 = plt.subplot() 314 ax1.contourf(x, y, z, levels=[-0.25, 0.25, 0.75, 1.25], colors=["blue", "white", "red"], alpha=0.3) 315 ax1.scatter(trainingData1[:, 0], trainingData1[:, 1], c="red", marker="o", s=10, label="training data - Positive") 316 ax1.scatter(trainingData0[:, 0], trainingData0[:, 1], c="blue", marker="o", s=10, label="training data - Negative") 317 ax1.scatter(testData1[:, 0], testData1[:, 1], c="red", marker="x", s=10, label="test data - Positive") 318 ax1.scatter(testData0[:, 0], testData0[:, 1], c="blue", marker="x", s=10, label="test data - Negative") 319 ax1.set(xlim=(0, 1), ylim=(0, 1), xlabel="$x_1$", ylabel="$x_2$") 320 plt.legend(loc="upper left", fontsize="x-small") 321 fig.tight_layout() 322 fig.savefig("pred.png", dpi=100) 323 plt.close() 324 325 326 327 if __name__ == "__main__": 328 lwlrObj = LWLR(trainingSet) 329 # tau = lwlrObj.search_tau() # 运算时间较长 ~ 目前搜索精度下最优值大约在tau=0.015043232844614693 330 cls = lwlrObj.get_cls((0.5, 0.5), tau=0.015043232844614693) 331 print(cls) 332 accuracy = lwlrObj.get_accuracy(testSet, tau=0.015043232844614693) 333 print("accuracy: {}".format(accuracy)) 334 spiralObj = SpiralPlot() 335 spiralObj.spiral_data_plot(trainingData0, trainingData1, testData0, testData1) 336 # spiralObj.spiral_pred_plot(lwlrObj, tau=0.015043232844614693) # 运算时间较长
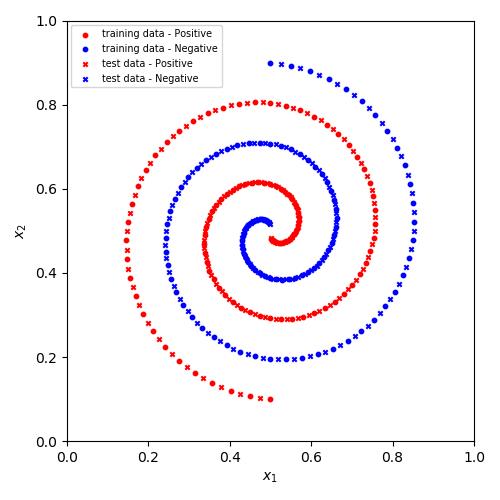很显然, 此螺旋数据集并非线性可分.
- 结果展示:
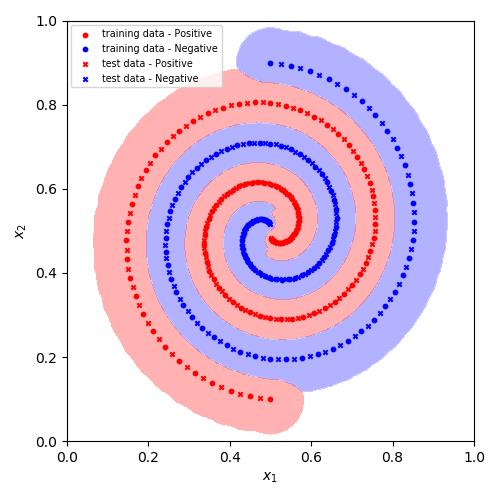此局部加权模型在训练集与测试集上的正确率均达到100%. - 使用建议:
①. 权重参数$\\tau$的获取极为关键, 很大程度上将影响模型的表达能力.
②. 泛化误差可能存在多个局部极值, 需要指定合适的范围, 再行采用黄金分割法进行搜索. - 参考文档:
螺旋数据集来源: https://www.cnblogs.com/tornadomeet/archive/2012/06/05/2537360.html
以上是关于局部加权之逻辑回归 - Python实现的主要内容，如果未能解决你的问题，请参考以下文章
斯坦福吴恩达教授机器学习公开课第三讲笔记——局部加权回归/线性回归的概率解释/分类和逻辑回归