局部加权回归法是啥

Posted 2023-04-13

局部加权回归方法(Lowess方法)作为一种较常见的基因芯片数据标准化方法涉及到众多的参数和权函数.对于权函数的选择一直以来都是采用三次权函数.因此从误差为重尾型的t分布出发,模拟不同自由度的基因芯片数据,然后选择不同的权函数对这些数据进行Lowess方法标准化,并利用残差平方和、标准化后的M和A值的相关系数及MA图作为评判标准,最终得到相关指标量与权函数的变化关系.
【相关链接】http://www.cnki.com.cn/Article/CJFDTOTAL-HZDX201001008.htm 参考技术A 　　局部加权线性回归法
　　对于一个数据集合(x0,y0),(x1,y1),⋯,(xm,ym)，我们预测它在x点时对应的y值时，如果采用的是传统的 线性回归模型，那么:
　　但是对于 局部加权线性回归(Locally Weighted Linear Regression)来说，在一定程度上可以避免上述问题，但是会付出一些计算量的代价。
　　局部加权线性回归(Locally Weighted Linear Regression)的过程是这样的:
　　其中w(i)是一个非负的权值，这个权值是用来控制每一个训练实例对于模型的贡献，假设要预测的点是x，则w(i)可以定义为:
　　w(i)=e−(x(i)−x)22τ2(1)

机器学习:局部加权线性回归(Locally Weighted Linear Regression)

线性回归

先复习一下线性回归的损失函数：

我们的目标是使该函数最小，用矩阵表示为：

对参数w求导得：

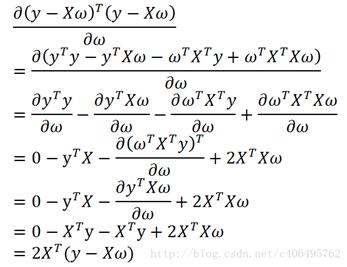
令上式等于0可估计出回归系数w得最优解：

但线性回归往往容易欠拟合，除了使用更复杂得函数拟合，还可以使用局部加权线性回归(locally weighted linear regression)

局部加权线性回归(LWLR)

在该算法中我们给待预测点附件得每个点赋予一定的权重，即在计算时我们更关注附近的数据，离的远的数据就不管了。
常使用高斯核来给数据点赋权重

高斯核

局部加权线性回归损失函数

同理，解的回归系数为损失函数对w求偏导，令偏导等于0求解w

回归系数

举个例子我们要拟合的数据如下，显然线性回归会欠拟合：

使用局部加权线性回归：

import matplotlib.pyplot as plt
import numpy as np
import math

data = np.loadtxt('ex0.txt')


def lwlr(testpoint, xArr, yArr, k):
    m = xArr.shape[0]   # 有多少行,200
    weights = np.mat(np.eye(m))  # (200,200)的单位矩阵
    for j in range(m):
        diffMat = testpoint - xArr[j, :]  # xArr的j行所有值
        weights[j, j] = np.exp(diffMat * diffMat.T / (-2.0*k**2))  # 这一直说我没对齐，卡了半天，最后把输入的X，mat一下就好了
    xTx = xArr.T * (weights * xArr)
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xArr.T * (weights * yArr.T))
    return testpoint * ws


def lwlrTest(testArr, xArr, yArr, k):
    m = testArr.shape[0]  # 样本数200
    yHat = np.zeros(m)  #
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat


X = np.mat(data[:, :2])
y = np.mat(data[:, -1])
yHat = lwlrTest(X, X, y, 0.01)  # 预测值yHat
srtInd = X[:, 1].argsort(0)  # 按特征的大小(x轴)排序,画折线图必须先排序, srtInd = [[151],[24]]
xSort = X[srtInd][:, -1]

plt.plot(xSort[:, -1], yHat[srtInd], c='r')
plt.scatter(data[:, -2], data[:, -1])
plt.show()

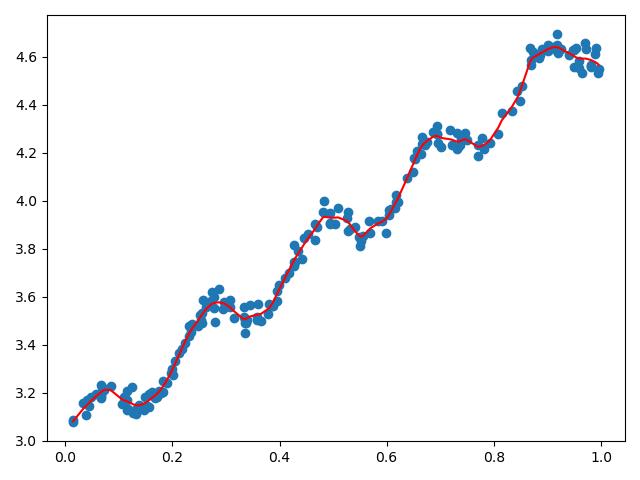
如果使用线性回归会欠拟合：