建立二叉树,层序、先序遍历
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了建立二叉树,层序、先序遍历相关的知识,希望对你有一定的参考价值。
建立二叉树,层序、先序遍历( 用递归或非递归的方法都可以)。
任务:要求能够输入树的各个结点,并能够输出用不同方法遍历的遍历序列;分别建立二叉树存储结构的输入函数、输出层序遍历序列的函数、输出先序遍历序列的函数。
麻烦高手给段代码 自己写了总是提示错误啊
最好用C啊 C++也可以呢
谢谢啊
这上面是我自己写的
二叉树的遍历方法之层序-先序-中序-后序遍历的简单讲解和代码示例
二叉树的基础性质及二叉树的建立参见前面两篇博文:
http://blog.csdn.net/why850901938/article/details/51052936
http://blog.csdn.net/why850901938/article/details/51052156
首先为了讲解方便,我建立了如图所示的二叉树:
取名为:树A
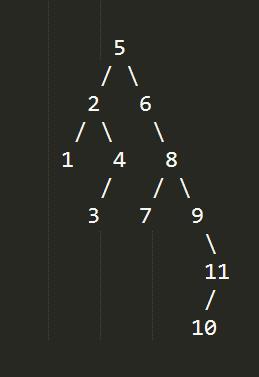
1.何为层序遍历?
层序遍历就是按照二叉树的层次由上到下的进行遍历,每一层要求访问的顺序为从左到右;
以树A为例,层序遍历得到的结果为:
5 2 6 1 4 8 3 7 9 11 10
2.何为先序遍历?
先序遍历的顺序为先到根节点,再到左节点,最后到右节点;
我们来看树A,首先从根节点5开始,先根输出5,然后左子树2,此时的位置在2,2相当于1和4两个结点的根,所以遍历2之后,先遍历2的左子树1,1没有子结点,所以遍历2的右子树4,4有左子树遍历3,这样完成了节点5的左子树遍历,再遍历5的右子树6,先遍历6的左子树,这里没有,就遍历6的右子树8,然后再遍历8的左右子树,左子树7,当然7没有孩子结点,所以接下来是9,然后 11 10类似。
最后我们得到先序遍历的结果为:
5 2 1 4 3 6 8 7 9 11 10
所以一定记住,访问根结点的操作发生在遍历其左右子树之前,在树A的例子中,访问完5之后访问2,接下来不是访问6,而是访问2的左右子树。
3.何为中序遍历?
中序遍历就是先到左子树、再到根节点、最后到右子树;
这时我们建立树B:
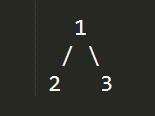
对树B而言,中序遍历就是 :
1 2 3
如果此时2节点有左右子树,那么我们建立树C:

此时对树C而言,中序遍历就是:
* 4 2 5 1 3 *
如果3节点有右子树而没有左子树,我们建立树D:

那么就是先访问3节点再访问6,结果为:
4 2 5 1 3 6
接下来回到我们的大家伙树A;
对于树A而言,其中序遍历的结果为:
1 2 3 4 5 6 7 8 9 10 11
对于开始情况,在访问5的时候,发现5有左子树2,先2,再访问2的时候发现有左子树1,所以肯定还是A1先,所以这个序列是从1开始的。
是不是感到很神奇了!没错在中序遍历中,根节点左边所有数都在其左子树上,右边所有数都是在其右子树上,这个性质有时解题会有用到;
4.何为后序遍历?
对于后序遍历而言,其访问顺序是先访问左节点,再访问右节点,最后才访问根节点;
对于树B:
后序遍历得到的结果是:2 3 1
对于树C:
后序遍历得到的结果是:4 5 2 3 1
对与树D:
后序遍历得到的结果是:4 5 2 6 3 1
回到大家伙树A:
其后序遍历得到的结果应是:
1 3 4 2 7 10 11 9 8 6 5
所以也可以看出在后序遍历中整颗数根节点是最后一个才遍历到的;
接下来重头戏到了,如何才能实现上述的四种遍历呢?
我们首先从层序遍历开始:
应当了解层序遍历其实是一种典型的基础BFS(宽度优先搜索)模型;
即以宽度为优先遍历对象,从左到右的遍历二叉树,实现方法应当使用队列,
即如图的平放管道模型,进出为单向通道:

队列是一种特性为FIFO(first in first out)的数据结构模型,根据这种特性,从整棵树的根节点开始,我们把每个根节点的左右节点依次压进队列中,根据先进先出特性,每次节点出来的顺序就是完全和层序遍历的顺序相同。
我们以树D为例进行讲解:
从1节点开始,首先压入1,对1进行压入左右节点的操作依次压入了2和3,
然后弹出1,接下来出来的是2,把2的左右节点4和5依次压入,弹出2,接着压入3,把的右节点6压入,弹出3,至此第二层的搜索结束,进入第三层,则依次遍历节点4 5 6 ,然后结束;
具体流程就是这样,接下来是层序遍历的代码讲解:
代码如下:
void BFS(Node *Root)
{
queue<Node*> Q;//队列的声明
Node * node ;
Q.push(Root);//先压入整棵树的根节点Root
while(!Q.empty())//如果队列不空则一直进行下去
{
node = Q.front();//访问队列的第一个元素
cout<<node->Value<<" ";//输出当前节点的值
if (node->Left!=NULL)
{
Q.push(node->Left); //如果左节点不为空则压入左节点
}
if (node->Right!=NULL)
{
Q.push(node->Right); //如果右节点不为空则压入右节点
}
Q.pop(); //弹出当前节点
}
cout<<endl;
}BFS代码引自同学博客:http://blog.csdn.net/u011613367/article/details/50950408
关于队列的基础操作和其他数据结构及STL的知识欢迎访问我的博文:
http://blog.csdn.net/why850901938/article/details/51052062
层序讲完了,接下来我们讲讲先序,中序,后序遍历的方法和代码:
简单来说先、中、后序遍历都使用DFS(深度优先搜索)的方法,在我的理解中深搜所用的方法就是递归,也就是自己调用自己的。为何使用递归?
我们结合代码进行讲解:
首先是先序遍历二叉树:
void PreOrderTraverse(BiTree T)
{
if(T)//如果当前节点不为空
{
printf("%d ",T->data); //先输出当前节点的值
PreOrderTraverse(T->Left); //再调用自己到左节点
PreOrderTraverse(T->Right);//最后到右节点
}
return;
}然后中序遍历:
void InOrderTraverse(BiTree T)
{
if(T)//如果当前节点不为空
{
PreOrderTraverse(T->Left); //先调用自己到左节点
printf("%d ",T->data); //再输出当前节点的值
PreOrderTraverse(T->Right); //最后到右节点
}
}最后后序遍历:
void PostOrderTraverse(BiTree T)
{
if(T)//如果当前节点不为空
{
PreOrderTraverse(T->Left); //先调用自己到左节点
PreOrderTraverse(T->Right); //再到右节点
printf("%d ",T->data); //最后输出当前节点的值
}
}主函数如下:
int main()
{
BiTree T;
int d;
T = CreateBiTree(); //建立二叉树
PreOrderTraverse(T); //先序遍历
printf("\\n");
InOrderTraverse(T); //中序遍历
printf("\\n");
PostOrderTraverse(T); //后序遍历
printf("\\n");
return 0;
}建立二叉树函数见:http://blog.csdn.net/why850901938/article/details/51052936
以上除注明引用处均为原创,图片均为自己所制作,转载请说明,给出链接就行~~~
仅代表个人观点,欢迎交流探讨,勿喷~~~

PhotoBy:WLOP
以上是关于建立二叉树,层序、先序遍历的主要内容,如果未能解决你的问题,请参考以下文章
二叉树的遍历方法之层序-先序-中序-后序遍历的简单讲解和代码示例
通过遍历序列构造二叉树(扩展二叉树的先序先序和中序后序和中序层序和中序)附可执行完整代码