二叉树的建立与遍历 两天之内就要，急用！！！！

Posted 2023-05-01

建立一颗二叉树，并对其进行遍历（先序，中序，后序），打印输出遍历结果。
要求：
1，从键盘接受输入（先序），以二叉链表作为存储结构，建立二叉树（以先序来建立），并采用算法对其进行遍历（先序，中序，后序），将遍历结果打印输出。
2，所用书籍按如下格式自行确定：
ABC##DE#G##F###（其中#表示空格字符）
则输出结果为：
先序：ABCDEGF
中序：CBEGDFA
后序：CGEFDBA

参考技术A #include<stdio.h>
#include <malloc.h>
#define maxsize 100
typedef char elemtype;
typedef struct Node

elemtype data;
struct Node *lchild;
struct Node *rchild;
BitNode;
void CreatBiTree(BitNode *&b,char *str)
BitNode *st[maxsize],*p=NULL;
int top=-1,k,j=0;
char ch;
b=NULL;
ch=str[j];
while(ch!='\0')
switch(ch)
case'(':top++;st[top]=p;k=1;break;
case')':top--;break;
case',':k=2;break;
default:p=(BitNode *)malloc(sizeof(BitNode));
p->data=ch;
p->lchild=p->rchild=NULL;
if(b==NULL)
b=p;
else
switch(k)
case 1:st[top]->lchild=p;break;
case 2:st[top]->rchild=p;break;
j++;
ch=str[j];



BitNode *Find(BitNode *b,elemtype x)
BitNode *p;
if(b==NULL)
return NULL;
else if(b->data==x)
return b;
else
p=Find(b->lchild,x);
if(p!=NULL)
return p;
else
return Find(b->rchild,x);



BitNode *Lchild(BitNode *b)
return b->lchild;

BitNode *rchild(BitNode *b)
return b->rchild;

int BiTreeDepth(BitNode *b)
/* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */
int i,j;
if(!b)
return 0;
if(b->lchild)
i=BiTreeDepth(b->lchild); //递归求左子树的深度
else
i=0;
if(b->rchild)
j=BiTreeDepth(b->rchild); //递归求右子树的深度
else
j=0;
return i>j?i+1:j+1; //取深度值大者加1作为该树的深度

void Visit(char ch)

printf("%c ",ch);


/*先序遍历二叉树*/
void PreOrder(BitNode *b)

if (b!=NULL)

Visit(b->data);
PreOrder(b->lchild);
PreOrder(b->rchild);



/*中序遍历二叉树*/
void InOrder(BitNode *b)

if (b!= NULL)

InOrder(b->lchild);
Visit(b->data);
InOrder(b->rchild);



/* 后序遍历二叉树*/
void PostOrder(BitNode *b)

if(b!= NULL)

PostOrder(b->lchild);
PostOrder(b->rchild);
Visit(b->data);



void main()

BitNode *b,*p,*lp,*rp;
printf("(1)用孩子链式储存结构创建二叉树");
CreatBiTree(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
printf("\n(2)输出'H'结点的左右孩子");
p=Find(b,'H');
if(p!=NULL)
lp=Lchild(p);
if(lp!=NULL)
printf("左孩子为:%c",lp->data);
else
printf("无左孩子");
rp=rchild(p);
if(rp!=NULL)
printf("右孩子为:%c",rp->data);
else
printf("无右孩子");
printf("\n");
printf("(3)二叉树b的深度为:%d\n",BiTreeDepth(b));
printf("(4)先序遍历序列为:");
PreOrder(b);
printf("\n(5)中序遍历序列为:");
InOrder(b);
printf("\n(6)后序遍历序列为:");
PostOrder(b);
printf("\n");
参考技术B 如果可以是用递归调用就很简单 如果用是用非递归调用 那就有点坑爹 参考技术C 二叉树的建立与遍历 两天之内就要，急用！！！！
ncludestdio.h 参考技术D #include <iostream.h>
#include <stdio.h>
#include <malloc.h>
#define MaxNode 100
typedef int ElemType;
typedef struct node

ElemType data;
struct node *lchild;
struct node *rchild;
BTNode;

void CreateTree(BTNode *&b,char *str)//建立一个二叉树

BTNode *St[100];
BTNode *p=NULL;
int top=-1,k,j=0;
char ch;
b=NULL;
ch=str[j];
while(ch!='\0')

switch(ch)

case '(':top++;St[top]=p;k=1;break;
case ')':top--;break;
case ',':k=2;break;
default:p=(BTNode *)malloc(sizeof(BTNode));
p->data=ch;
p->lchild=p->rchild=NULL;
if(b==NULL)
b=p;
else

switch(k)

case 1:St[top]->lchild=p;break;
case 2:St[top]->rchild=p;break;



j++;
ch=str[j];



void PreOrder(BTNode *b)//前序遍历

if(b!=NULL)

printf("%c ",b->data);
PreOrder(b->lchild);
PreOrder(b->rchild);



void InOrder(BTNode *b)//中序遍历


BTNode p,stack[MaxNode];
int top=0;
if(b==NULL) return;
p=*b;
while(!(p == NULL && top == 0))

while(p!=NULL)


if(top<MaxNode-1)stack[top]=p;top++;
elseprintf("栈溢出");return;
p=p->lchild;

if(top<=0)return;
elsetop--;p=stack[top];printf("%c",root->data);p=p->rchild;



void LaOrder(BTNode *b)//后序遍历

if(b!=NULL)

LaOrder(b->lchild);
LaOrder(b->rchild);
printf("%c ",b->data);


void main()

int number;
BTNode *b=NULL;
cout<<" 【1】创建树"<<endl<<endl;
cout<<" 【2】先序遍历树"<<endl<<endl;
cout<<" 【3】中序遍历树"<<endl<<endl;
cout<<" 【4】后序遍历树"<<endl<<endl;
cout<<" 【5】结束"<<endl<<endl<<endl;
cout<<"请输入您的选择"<<endl;
cin>>number;
while(number!=5)


if(number==1)

char str[100];
printf("请输入：");
scanf("%s",&str);
CreateTree(b,str);
printf("树创建成功!\n");

else if(number==2)

if(b==NULL)

printf("对不起，您还没有创建树!\n");

else

PreOrder(b);
printf("\n");


else if(number==3)

if(b==NULL)

printf("对不起，您还没有创建树!\n");

else

InOrder(b);
printf("\n");


else if(number==4)

if(b==NULL)

printf("对不起，您还没有创建树!\n");

else

LaOrder(b);
printf("\n");


printf("请输入您的选择:\n");
scanf("%d",&number);



最佳答案 中序遍历有问题：改后如下
void InOrder(BTNode *b)//中序遍历


BTNode *p,*stack[MaxNode];
int top=0;
if(b==NULL) return;
p=b;
while(!(p == NULL && top == 0))

while(p!=NULL)


if(top<MaxNode-1)stack[top]=p;top++;
elseprintf("栈溢出");return;
p=p->lchild;

if(top<=0)return;
elsetop--;p=stack[top];printf("%c",p->data);p=p->rchild;

本回答被提问者采纳

Python --- 二叉树的层序建立与三种遍历

二叉树（Binary Tree）时数据结构中一个非常重要的结构，其具有。。。。（此处省略好多字）。。。。等的优良特点。

之前在刷LeetCode的时候把有关树的题目全部跳过了，（ORZ：我这种连数据结构都不会的人刷j8Leetcode啊！！！）

所以 ！！！敲黑板了！！！今天我就在B站看了数据结构中关于树的内容后，又用我浅薄的Python大法来实现一些树的建立和遍历。

---

关于树的建立我觉得层序建立对于使用者来说最为直观，输入很好写。（好吧，我是看LeetCode中的树输入都是采用层序输入觉得非常好）

树节点定义

代码来

class BSTreeNode(object):
    def __init__(self, data):
        self.val = data
        self.leftChild = None
        self.rightChild = None

这一段代码太好理解了好吧，就不BB了。

二叉树层序建立

不多说，先上代码

 1 # 建立二叉树是以层序遍历方式输入，节点不存在时以 ‘None‘ 表示
 2 def creatTree(nodeList):
 3     if nodeList[0] == None:
 4         return None
 5     head = BSTreeNode(nodeList[0])
 6     Nodes = [head]
 7     j = 1
 8     for node in Nodes:
 9         if node != None:
10             node.leftChild = (BSTreeNode(nodeList[j]) if nodeList[j] != None else None)
11             Nodes.append(node.leftChild)
12             j += 1
13             if j == len(nodeList):
14                 return head
15             node.rightChild = (BSTreeNode(nodeList[j])if nodeList[j] != None else None)
16             j += 1
17             Nodes.append(node.rightChild)
18             if j == len(nodeList):
19                 return head

 

 

 creatTree即为层序建立二叉树的函数，传入的参数为一个层序遍历的数组，就是将树节点从左往右，从上往下一次放入数组中，如果某个节点不存在则用None来表示。

比如：

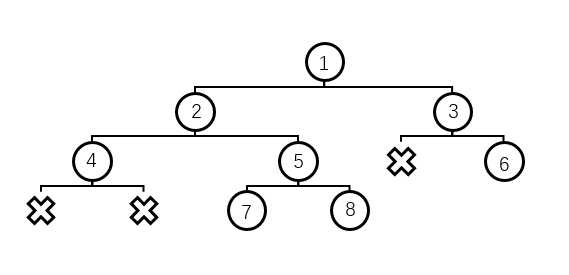图所示的二叉树则需输入a = [1,2,3,4,5,None,6,None,None,7,8]，接下来将会以这个二叉树为例讲解代码。

• 第3-4行，判断根节点是否为空。 如果根节点都为空，那树（shuo）就（ge）不（j）存（8）在了，直接返回就好了。
• 第5行，将元素列表中的第一个元素取出新建根节点，最后返回的即为根节点
• 第6行，创建了一个Nodes列表中，用于存放树中的节点，每生成一个节点就将其放入该列表中，可以看成是一个队列（这么说好像也不是特别规范，因为后面只是取列表中的元素，没有弹出首元素），此处将根节点存入。
• 第7行，创建变量j用于nodeList中元素的索引，初始为1.因为第0个元素已经创建根节点了。
• 第8行，依次取出Nodes列表中的节点，对其创建左子节点和右子节点
• 第9行，首先判断取出的Nodes是否为空，如果为空，说明此处没有节点，就无需创建子节点，否则进行子节点的创建
• 第10行，为该节点创建左节点，其值就是索引j的所对应的值，如果nodeLists[j] == None 说明没有该子节点，就不用创建了，即Child = None
• 第11行，将新建的节点加入Nodes数组，使其在for循环中可以继续为其添加子节点
• 第12行，j加1，这样刚好使每一个nodeList的元素对应一个节点了
• 第13行，判断j的值，如果与nodeList值相等说明全部节点已经添加完毕了，直接返回head根节点就完成了树的建立
• 第15-19行，为节点添加右节点，与添加左节点的逻辑是一样的，就不在赘述了

好了代码注释完毕，我们再通过结合实例来解释一下：

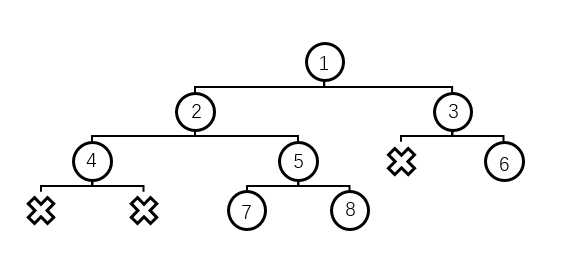•  nodeList = [1,2,3,4,5,None,6,None,None,7,8],下面节点统一用n(值)来表示
• 建立根节点 head = n(1), j=1, len(nodeList) = 11
• 开始for循环：Nodes = [n(1)]
  • node为n(1)，非空
    • nodeList[j]=nodeList[1]=2 非空，所以新建节点n(2),n(1)的左节点即为n(2),新建节点放入Nodes, 则Nodes=[n(1),n(2)] j+1=2, j未溢出
    • nodeList[j]=nodeList[2]=3 非空，所以新建节点n(3),n(1)的右节点即为n(3),新建节点放入Nodes, 则Nodes=[n(1),n(2),n(3)], 然后j+1=3, j未溢出
  • node为n(2)，非空
    • nodeList[j]=nodeList[3]=4 非空，所以新建节点n(4),n(2)的左节点即为n(4),新建节点放入Nodes, 则Nodes=[n(1),n(2),n(3),n(4)], j+1=4, j未溢出
    • nodeList[j]=nodeList[4]=5 非空，所以新建节点n(5),n(2)的右节点即为n(5),新建节点放入Nodes, 则Nodes=[n(1),n(2)，n(3),n(4),n(5)], j+1=5, j未溢出
  • node为n(3)，非空
    • nodeList[j]=nodeList[5]=None 为空，所以n(3)的左节点直接等于None, 同时将None也放入Nodes, 则Nodes=[n(1),n(2)，n(3),n(4),n(5),None] j+1=6, j未溢出
    • nodeList[j]=nodeList[6]=6 非空，所以新建节点n(6),n(3)的右节点即为n(6),新建节点放入Nodes, 则Nodes=[n(1),n(2)，n(3),n(4),n(5),None,n(6)], j+1=7, j未溢出　
  • node为n(4),非空
    • nodeList[j]=nodeList[7]=None 为空，所以n(4)的左节点直接等于None,同时将None也放入Nodes, 则Nodes=[n(1),n(2)，n(3),n(4),n(5),None,n(6),None], j+1=8, j未溢出
      
    • nodeList[j]=nodeList[8]=None 为空，所以n(4)的右节点直接等于None,同时将None也放入Nodes, 则Nodes=[n(1),n(2)，n(3),n(4),n(5),None,n(6),None，None], j+1=9, j未溢出
  • node为n(5), 非空
    • nodeList[j]=nodeList[9]=7 非空，所以新建节点n(7),n(5)的左节点即为n(7),新建节点放入Nodes, 则Nodes=[n(1),n(2)，n(3),n(4),n(5),None,n(6),None，None，n(9)] j+1=10, j未溢出
      
    • nodeList[j]=nodeList[10]=8 非空，所以新建节点n(8),n(5)的右节点即为n(8),新建节点放入Nodes, 则Nodes=[n(1),n(2)，n(3),n(4),n(5),None,n(6),None，None，n(9)，n(10)] j+1=11, j溢出
• j溢出，则返回head根节点，结束二叉树的建立

　　PS：如果node为空节点的话，就会直接跳过空节点。

 

二叉树遍历（神用的递归）

1. 前序遍历

 

#head为二叉树的根节点
def PreorderTraverse(head):
    if head:
        print(head.val)
        PreorderTraverse(head.leftChild)
        PreorderTraverse(head.rightChild)

 

 

2. 中序遍历

 

#head为二叉树的根节点
def InorderTrverse(head):
    if head:
        InorderTrverse(head.leftChild)
        print(head.val)
        InorderTrverse(head.rightChild)

  

 

3. 后续遍历

#head为二叉树的根节点
def PostorderTraverse(head):
    if head:
        PostorderTraverse(head.leftChild)
        PostorderTraverse(head.rightChild)
        print(head.val)

 

 对中序遍历，费了我九牛二虎之力画了一个程序执行的图，红色箭头代表程序执行的过程，依然以a = [1,2,3,4,5,None,6,None,None,7,8]为例

 

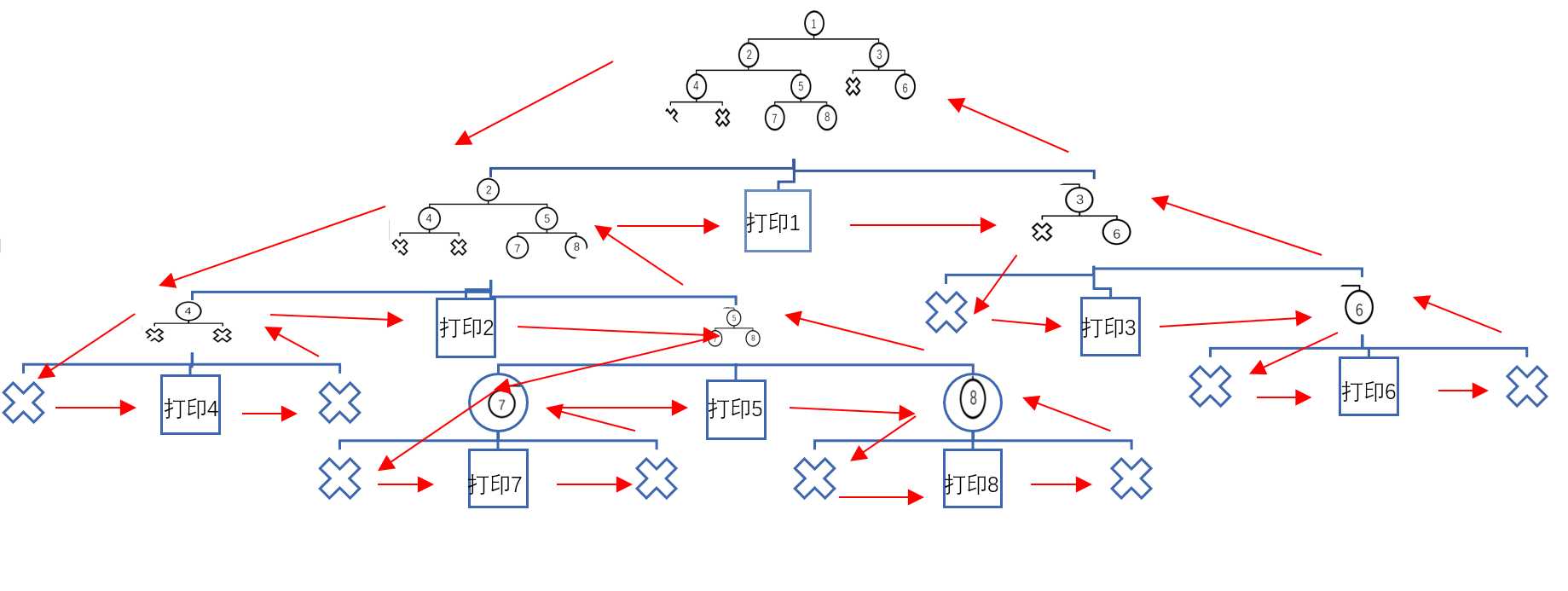
所以程序打印出来的顺序为：4 2 7 5 8 1 3 6

---

 

最后，致敬大佬，祝各位学有所成。

 

【转载表明出处，谢谢】