如何用牛顿迭代法求解方程
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何用牛顿迭代法求解方程相关的知识,希望对你有一定的参考价值。
牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。另外该方法广泛用于计算机编程中。设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0)+f'(x0)(x-x0),求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0),称x1为r的一次近似值。过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f'(x1),称x2为r的二次近似值。重复以上过程,得r的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r的n+1次近似值,上式称为牛顿迭代公式。
解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。把f(x)在x0点附近展开成泰勒级数 f(x) = f(x0)+(x-x0)f'(x0)+(x-x0)^2*f''(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x-x0)=f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。 参考技术A 你要的应该是这个咯!!!
牛顿迭代法:
#include<stdio.h>
#include<conio.h>
#include<math.h>
#define MAXREPT 1000
float f(float x)
return(x-exp(-x));
float df(float x)
return(1+exp(-x));
float iterate(float x)
float x1;
x1=x-f(x)/df(x);
return(x1);
void main()
float x0,x1,eps,d;int k=0;
printf("\n please input x0,eps:");
scanf("%f,%f",&x0,&eps);
printf("\n k xk\n");
printf(" %d %f\n",k,x0);
do
k++;
x1=iterate(x0);
printf(" %d %f\n",k,x1);
d=fabs(x1-x0);
x0=x1;
while((d>=eps)&(k<MAXREPT));
if(k<MAXREPT)
printf("the root is x=%f, k=%d\n",x1,k);
else
printf("\n The iteration is failed!\n");
getch();
参考技术B 随便找本数值计算方法书就行了
给你个资料吧,百度百科的
牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。另外该方法广泛用于计算机编程中。
设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0)+f'(x0)(x-x0),求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0),称x1为r的一次近似值。过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f'(x1),称x2为r的二次近似值。重复以上过程,得r的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r的n+1次近似值,上式称为牛顿迭代公式。
解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。把f(x)在x0点附近展开成泰勒级数 f(x) = f(x0)+(x-x0)f'(x0)+(x-x0)^2*f''(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x-x0)=f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。
[数值计算-7]:一元n次非线性方程求解-单点盲探-牛顿迭代法&Python法代码示例
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119813740
目录
1. 一元n次非线性方程
1.1 非线性函数
线性函数是一次函数的别称,则非线性函数即函数图像不是一条直线的函数。
非线性函数包括指数函数、幂函数、对数函数、多项式函数等等基本初等函数以及他们组成的复合函数
1.2 非线性函数案例
y = f(x) = a3*x^3 + a2*x^1 + a0
另a3 = 1, a2=-1, a0=-1;得到:
y=f(x) = x^3 - x^2 - 1
1.3 非线性函数的几何图形

2. 牛顿迭代法求非线性方程解的基本原理
2.1 概述
牛顿迭代法(Newton's method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

2.2 中值定理

中值定理是反映函数本身与其在某一点处的导数之间联系的重要定理。
函数与其导数是两个不同的函数;而导数只是反映函数在一点的局部特征;如果要了解函数在其定义域上的整体性态,就需要在导数及函数间建立起联系,微分中值定理就是这种作用。
微分中值定理,包括罗尔定理、拉格朗日定理、柯西定理、泰勒定理。是沟通导数值与函数值之间的桥梁,是利用导数的局部性质推断函数的整体性质的工具。
拉格朗日中值定理:
内容是说一段连续光滑曲线中必然有一点,它的斜率与整段曲线平均斜率相同。
 上述公式既是牛顿迭代法误差公式的基础,也是迭代公式的基础。
上述公式既是牛顿迭代法误差公式的基础,也是迭代公式的基础。
2.3 确定误差或收敛条件

当X接近真实根的时候,X与真实值的误差约等于Xk+1与Xk之间的差值。
2.4 迭代过程


2.5 牛顿迭代法的条件
(1)在真实解附近是可导
(2)初始值需要靠近真实解附近
2.6 牛顿迭代法的优缺点
(1)优点:
-
在真实解附近,收敛快
-
能够体现导数对迭代收敛意义和作用
(2)缺点:
如果初始点离真实解较远,且中间的单调的,就可以切线与X轴的交点,不能向真实解收敛,即y=f(x)不能向0方向收敛。因为所谓求方程解,就是求y=f(x)=0处的x值,如果y=f(Xk)不能向0收敛,则x就无法向真实解收敛。
解决次问题的方法:就是“牛顿下山法”对牛顿迭代法进行优化和限制。
3. Python代码示例
3.1 案例1:初值= +2
(1)源代码:
#导入库
from math import *
import time
import numpy
import matplotlib.pyplot as plt
# 一元N次非线性函数
# y=f(x) = x^3 - x - 1
def f(x,derive):
#定义函数参数
if(derive == 0):
return(1.0*x**3 - 1.0*x**1 -1) #原函数
elif (derive == 1):
return(3.0*x**2 - 1.0) #导函数
else:
print("Input Error")
return(0)
#定义精度
accuracy = 0.0001
#定义起始点
x1 = 2
#log data
count = 0
x_data = []
y_data = []
#记录初始节点
x_data.clear()
y_data.clear()
x_data.append(0)
y_data.append(x1)
#迭代起始时间
start = time.time()
while True:
#新的一轮迭代
x2 = x1 - f(x1,0)/f(x1,1) # X值的迭代
Err = fabs(x2-x1) # 迭代后误差
x1 = x2 # 保留当前x值
#增加log记录
count = count + 1
x_data.append(count)
y_data.append(x1)
if (Err <= accuracy):
break;
#迭代终止时间
end = time.time()
print("耗时=", end-start)
print("迭代次数=", count)
print("方程解=", x2)
print("实际误差=", Err)
print("迭代数据序列..........")
print("\\n迭代过程")
for x in x_data:
print("X{}={}".format(x,y_data[x]))
plt.scatter(x_data, y_data)(2)输出结果
耗时= 0.00099945068359375
迭代次数= 5
方程解= 1.3247179572458576
实际误差= 1.0921712676470463e-06
迭代过程
X0=2
X1=1.5454545454545454
X2=1.359614915915184
X3=1.325801345005845
X4=1.3247190494171253
X5=1.3247179572458576(3)图形显示收敛过程
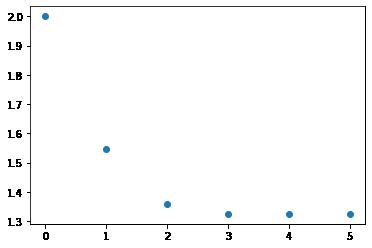
3.1 案例2:初值= -2
(1)源代码
#定义精度
accuracy = 0.0001
#定义起始点
x1 = -2
#log data
count = 0
x_data = []
y_data = []
#记录初始节点
x_data.append(0)
y_data.append(x1)
#迭代起始时间
start = time.time()
while True:
#新的一轮迭代
x2 = x1 - f(x1,0)/f(x1,1) # X值的迭代
Err = fabs(x2-x1) # 迭代后误差
x1 = x2 # 保留当前x值
#增加log记录
count = count + 1
x_data.append(count)
y_data.append(x1)
if (Err <= accuracy):
break;
#迭代终止时间
end = time.time()
print("耗时=", end-start)
print("迭代次数=", count)
print("方程解=", x2)
print("实际误差=", Err)
print("\\n迭代过程")
for x in x_data:
print("X{}={}".format(x,y_data[x]))
plt.scatter(x_data, y_data)(2)输出
耗时= 0.0
迭代次数= 65
方程解= 1.3247179574157972
实际误差= 1.3548153629638904e-05
迭代过程
X0=-2
X1=-1.3636363636363638
X2=-0.8892353134230391
X3=-0.29609491722682657
X4=-1.2864352364252927
X5=-0.8217128731113184
X6=-0.10691984835296464
X7=-1.03298211799929
X8=-0.5472085094190648
X9=-6.611274711607757
X10=-4.433702585989313
X11=-2.989538057557567
X12=-2.031496813533126
X13=-1.3854649531667529
X14=-0.9075970552862211
X15=-0.33661987193684095
X16=-1.3994357597139493
X17=-0.9192055355939536
X18=-0.3605283713478141
X19=-1.4855582794693762
X20=-0.9886592503827742
X21=-0.4826912520186133
X22=-2.5747641103691308
X23=-1.7544435797503293
X24=-1.190229561606389
X25=-0.7299425321629264
X26=0.37120956464817956
X27=-1.8791055025333052
X28=-1.2790826744313537
X29=-0.8150369612962106
X30=-0.08343010635041948
X31=-1.0201408804244034
X32=-0.5293414717824825
X33=-4.4127113786720065
X34=-2.9756275206939176
X35=-2.0222349844904874
X36=-1.3790536473294959
X37=-0.9022331545785207
X38=-0.3251428738220351
X39=-1.3637814489635551
X40=-0.8893583038994928
X41=-0.2963784747231665
X42=-1.2871128668662455
X43=-0.822325743167123
X44=-0.10902119046333758
X45=-1.0342878895057943
X46=-0.5489915337873275
X47=-6.9822885227693545
X48=-4.680020332909626
X49=-3.1527764448637754
X50=-2.140083129871087
X51=-1.4602171044569312
X52=-0.9685635995638602
X53=-0.4504371240959939
X54=-2.0883677454698484
X55=-1.4247054725546997
X56=-0.9399406438426444
X57=-0.40040427420864433
X58=-1.6793109477226182
X59=-1.1355642957994752
X60=-0.6723450974394425
X61=1.1010597171365635
X62=1.3916209468034497
X63=1.3285408122104765
X64=1.3247315055694269
X65=1.3247179574157972(3)图形

作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119813740

以上是关于如何用牛顿迭代法求解方程的主要内容,如果未能解决你的问题,请参考以下文章