理解SVM模型的目标函数

Posted 2023-04-04

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了理解SVM模型的目标函数相关的知识，希望对你有一定的参考价值。

参考技术A 《Hands-on Machine Learning with Scikit-Learn, Keras and TensorFlow》一书5.4节《Under the Hood》在解释SVM模型的数学模型时，有些地方并不是很详细。这里我把相关的知识补上。关于SVM，这篇文章有比较详细的解释，有兴趣的朋友可以参考。

我们假设样本线性可分，一类标记为1，另一类标记为-1。每个样本可用向量表示。则我们可以找到一个超平面，使得超平面的一侧都是正类样本，另一侧都是负类样本。这个超平面（不妨称为平面0）可以用下面这个方程式表示：

我们可以把这个超平面向正类样本方向平移，直到碰到第一个正类样本为止。平移完成之后新的超平面我们可以称为平面1，其方程是：

同理，我们把平面0向负类样本方向平移，直到碰到第一个负类样本为止。平移完成之后新的超平面我们可以称为平面2，其方程是：

和并不一定相等，不过我们可以调整平面0的b，使得。也就是说，通过选择适当的b，我们可以使得平面1和平面2的方程可以写成下面的形式：

事实上，这两个方程还可以进一步化简。我们让两个式子两边都除以，也就是调整了和。这样，平面1和平面2的方程可以写成：

这两个平面的距离是。因此，我们优化的目标就是使得最小。

当然，我们还有约束条件，就是上面的平面能够使得所有正负样本正好在平面两侧，这就是所谓硬间隔SVM（Hard margin linear SVM）。用数学语言说，对于任意正样本i，我们有：

对于任意负样本i，我们有：

我们定义，规则是，对于正样本，其值为1；对于负样本，其值为-1。于是，上面两个约束条件可以合并为一个：

这就是约束条件。于是：

这就是Hard margin linear SVM模型的优化目标。

如何分分钟理解SVM（中文版）

前言

先前我们已经说了说了一下SVM算法，并且简单的实现了一下SVM算法，但是先前的版本是英文版本的，所以现在开放中文版。由于先前的英文版本是自己直接硬写的，然后自行查词汇，词典写出来的，但是受限于自己的水平，所以有很多问题，可能连表述也具备误导性，因此现在开放中文版本，并且对先前的一些内容进行补充说明。

本文目标：

1. SVM基本数学推导
2. 基于Python实现SVM算法

涉及概要：

拉格朗日
高数求导（偏导）
基本几何空间向量知识
Python基础语法
逻辑抽象能力

(注：为了更好理解，本文顺序将和原英文版顺序不同，并且删减了一些部分，使得内容更加简练）
此外本博文针对的是基于统计机器学习的一些经典算法。

算法简介

在开始之前我们先简单介绍一下SVM算法，这个算法是非常经典的一个分类算法，用于二分类处理，算法，通过将我们的数据映射到一个解的超空间内，之后通过超平面将我们的数据划分为两个空间从而实现对对象的分类。

例如下面的例子：

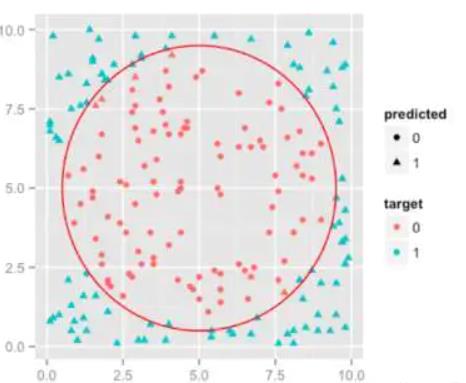
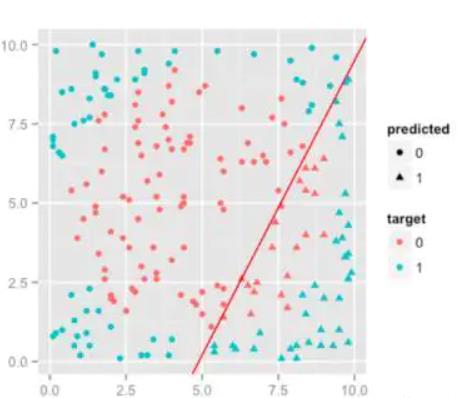
我们将数据映射到一个二维平面，之后使用到一种超平面将这些玩意进行划分。当然在想要实现上面的这张图片的效果，我们是需要使用到核函数的，实际上在一个单纯的二维平面上得到的结果可能是像下面这样的：

数据标签

在正式开始我们的算法之旅之前请让我在复述一遍它的数据格式，也就是数据标签的格式。

我们这这里主要是说明一下，在实际上送进我们算法里面的数据标签到底是咋样的。
（如下图：）

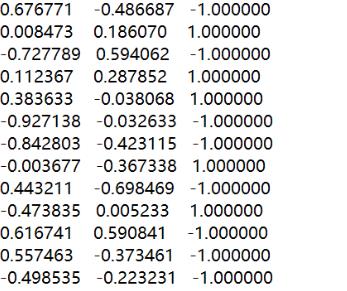
首先前两者是我们的feature，后面那个1，-1则是我们实际的一个类别。

也许在你实际上的数据是这样的。

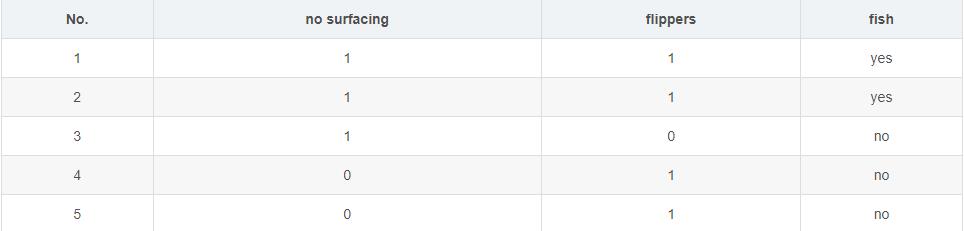
yes表示1，no表示-1

但是在我们送入算法的时候，我们是要把标签进行映射的，当然这个其实也是常识，只是在这里我想说明的是，他送进算法的数据用于训练的是长这个样子的。

算法核心

其实关于SVM这个算法，其实本质上并不难，只是里面涉及的数学知识比较多罢了，当然这也是我现在去手写一些算法的乐趣，因为它在极大程度上激励了我去学习数学，并且准备接下来将面对的考研。

首先，我们整个算法的目的只有一个，那就是我们需要找到一个超平面，把我们的数据可以划分为两个类。如果你使用了高斯核函数（假设你只有两个feature）那么你可能看到的情况是这样的：

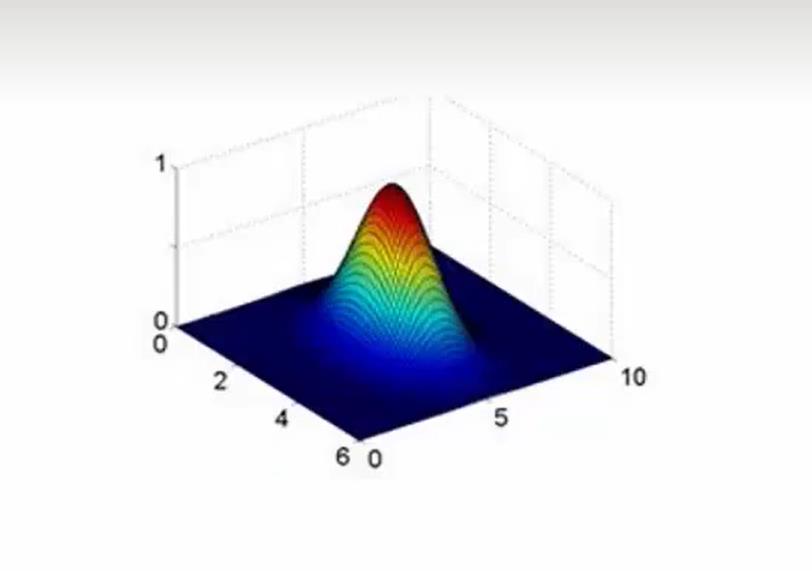
然后又一给平面把这玩意划分为了两个部分（图上没有画出那个平面，实在没找到图）

之后当新的数据进入的时候，我们将判断这个点是在平面的上面还是下面，上面为正例，反之为负例。

例如我们得到一个超平面 Ax+By+C = 0（用矩阵表示就是 Wx+B = 0)

之后有一个点 a b 将这个点带入这个平面，如果大于0自然就是上面反之。

那么最后通过我们的推导呢，我们会得到这样的一个方程：

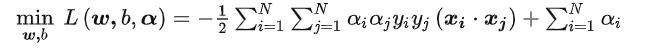
我们将求解出这个方程的最小值，也就是得到α的值。

然后结合这两个方程：

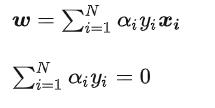
求解出w,b 也就是超平面 feature 的系数和偏置。

所以说，咱们这个实际上的SVM算法其实是用某一种启发式算法来求解出上面的最小值的方程，然后得到对应的W，B。
之后嘿嘿。

所以，想要代码的同学，直接找到咱们本文的代码部分，copy就完了，因为我们做的一件事就是刚刚说的，里面使用到一个启发算法解方程（SMO算法），然后就完了，只是后面做了一些处理罢了。

理论推导

这部分的内容比较复杂，可以跳过。这里也是重新整理了一下，找到了更加专业的解释说明刚好弥补一下咱们先前的版本。

那么我们先来简单一点的推导：

问题转换

SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示，即为分离超平面，对于线性可分的数据集来说，这样的超平面有无穷多个（即感知机），但是几何间隔最大的分离超平面却是唯一的。

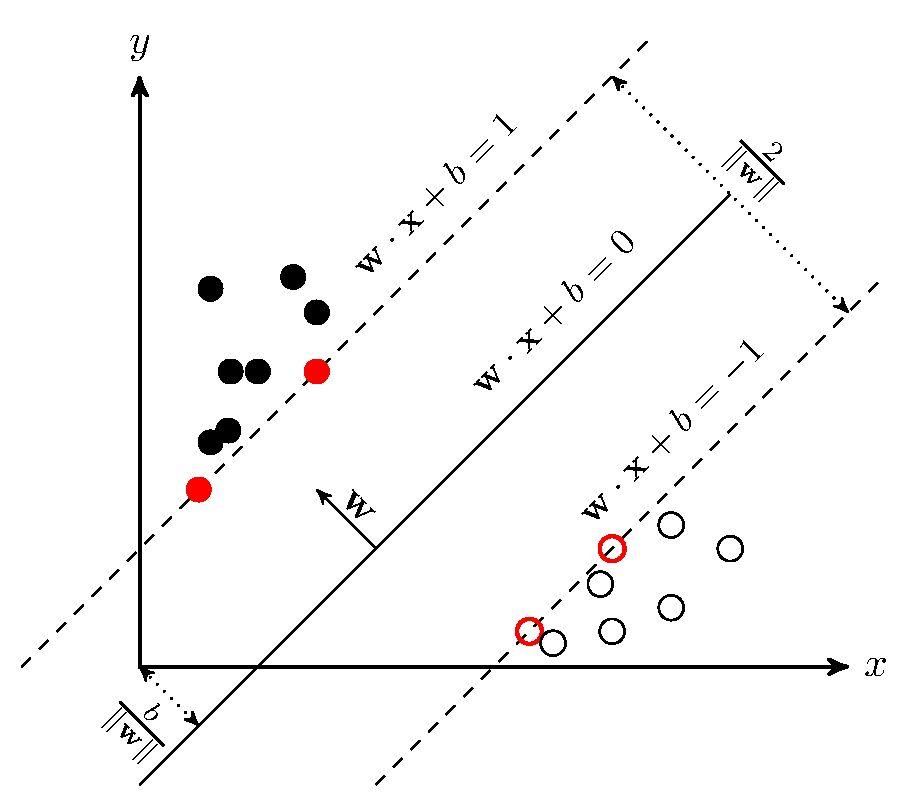
在推导之前，先给出一些定义。假设给定一个特征空间上的训练数据集，我们将正例记作+1 反之为-1.

也就是这样的数据：

之后我们将假设一个平面，之后计算每一个点到平面的距离。

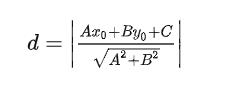
用矩阵表示就是这样的：

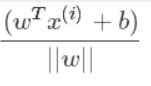
注意这里其实是由绝对值的（没有找对这样的图，先凑合一下）

所以为了方便计算，在结合我们原来的定义，如果将点带入超平面，得到的值是>0的就是+1 反之-1，所以我们乘以对应的标签值，就可以得到绝对值。

所以我们将得到这样的方程：

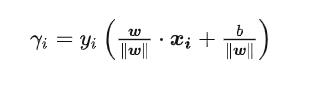
这个就是咱们的距离，我们得到其中最小的距离：

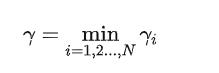
之后我们想办法让这个玩意最大：

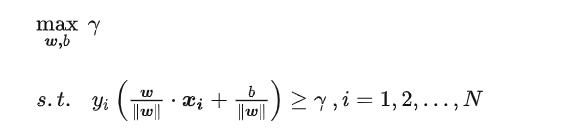
在这个约束条件下让这个玩意最大化。
其实这里表示的就是一个意思：找到一个，平面能够让离这个平面最近的点到平面的距离最大。

将约束条件两边同时除以 γ ，得到：

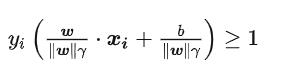
之后我们对W和γ进行约简，因为他们都是标量：

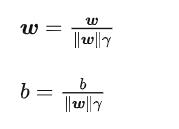
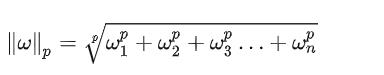
又因为最大化 γ ，等价于最大化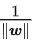也就等价于最小化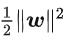（ 1/2 是为了后面求导以后形式简洁，不影响结果），因此SVM模型的求解最大分割超平面问题又可以表示为以下约束最优化问题.

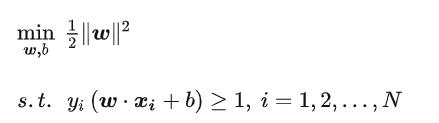
目标求解

现在我们得到了这个玩意，那么接下来就是如何求解这个带有二次约束优化的问题。

所以这里引入拉格朗日求解，问题转化为：

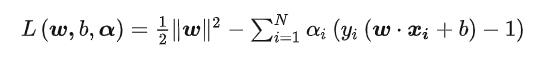
α为拉格朗日乘子>0

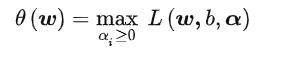
其中我们的页数条件依然是：

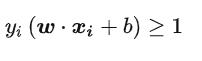
如果是这样，那么就不满足我们的可行解：

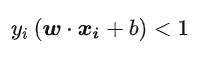
当我们的点不满足可行解的时候，我们将其的W设置为无穷大。因为我们需要的是支持向量，也就是满足条件的向量带入我们的距离进行运算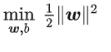，设置围殴无穷大那么这个点就不再起到作用。

因此：

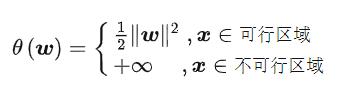
问题转化为：

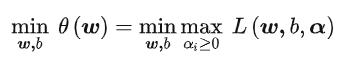
这个求解过程不好做。所以，我们需要使用拉格朗日函数对偶性，将最小和最大的位置交换一下，这样就变成了：

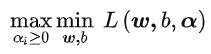
KTT条件

这个主要是咱们拉格朗日的问题，刚刚咱们是使用到了一个对偶性质，所以在实际的情况下，他是这样的：

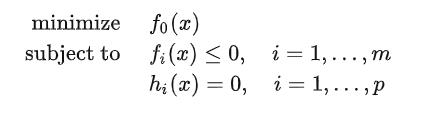
只有这样，它的这个拉格朗日是这样的：

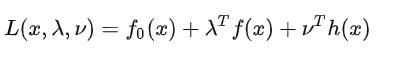
这不就是咱们刚刚的目标方程嘛。

这里咱们先不考虑这个，属于高数范畴，我也还在恶补当中，也很难展开。

所以最后咱们是这样的：
转化之后，要满足这个条件：

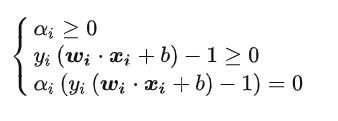
之后，求取最小值的话，我们求得偏导就好了，对w和b求偏导，让他等于0就得到了解。

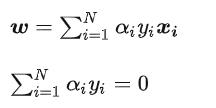
（这里其实还有b，但是稍等，后面再推导出来）

之后展开

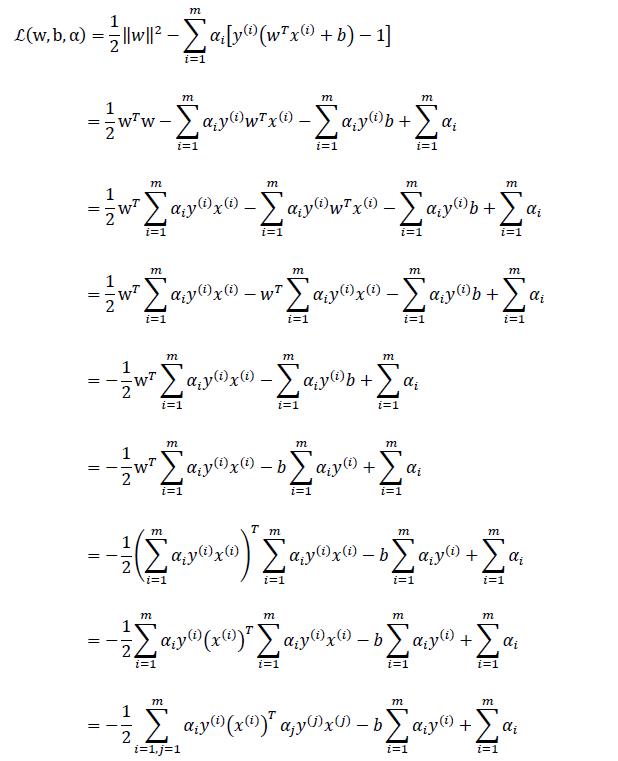
化简：

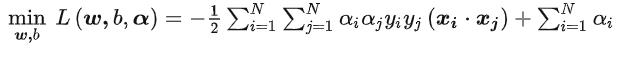
由于我们的目标是求解出α，求出最大的α让这个玩意最小。

所以问题转化：

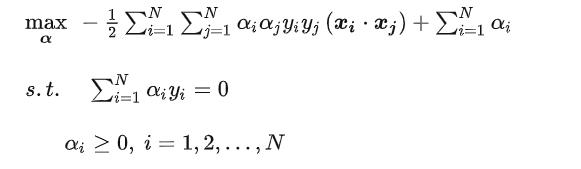
之后求最大值转化为最小值：

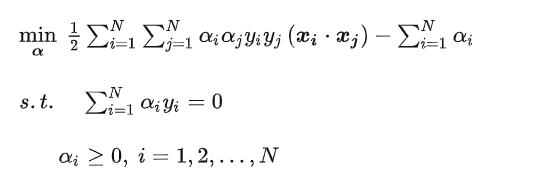
转换平面

现在我们可以求解α，但是我们最终需要的W，B，其中W我们前面推导出来了。

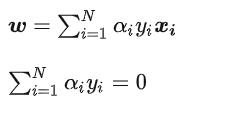
并且还有这样的条件：

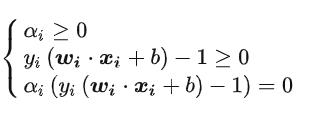
由于W！=0
所以最终可以得到：

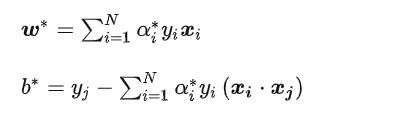
简单案例

这里面还是引用先前一个视频的案例：

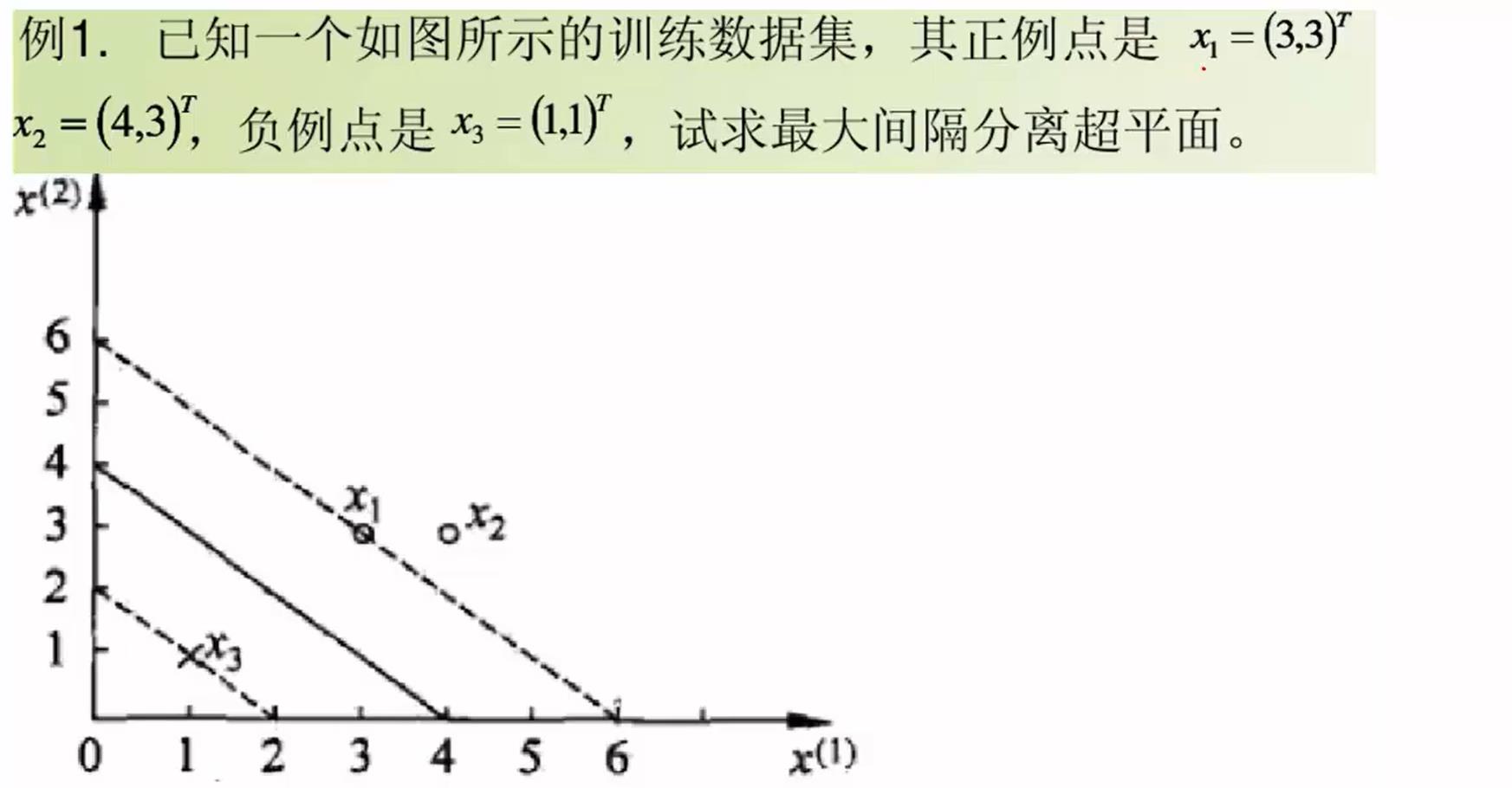
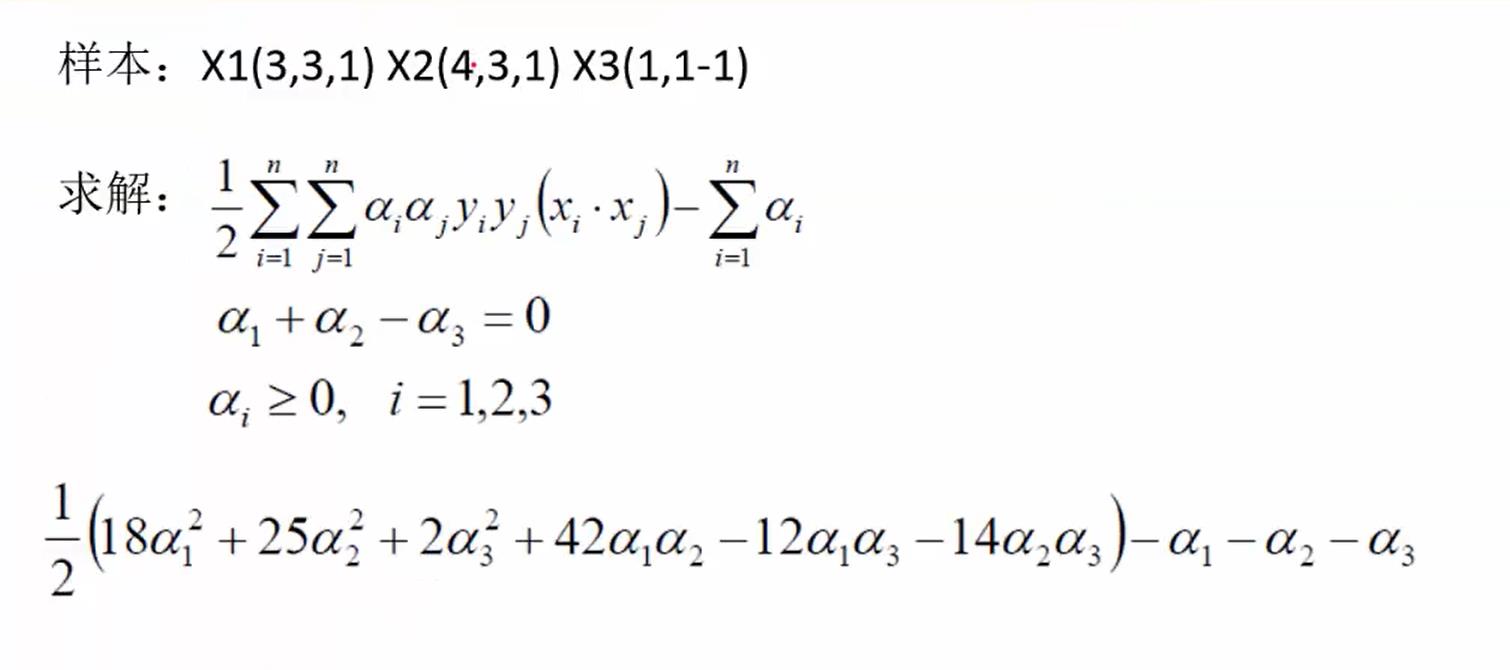
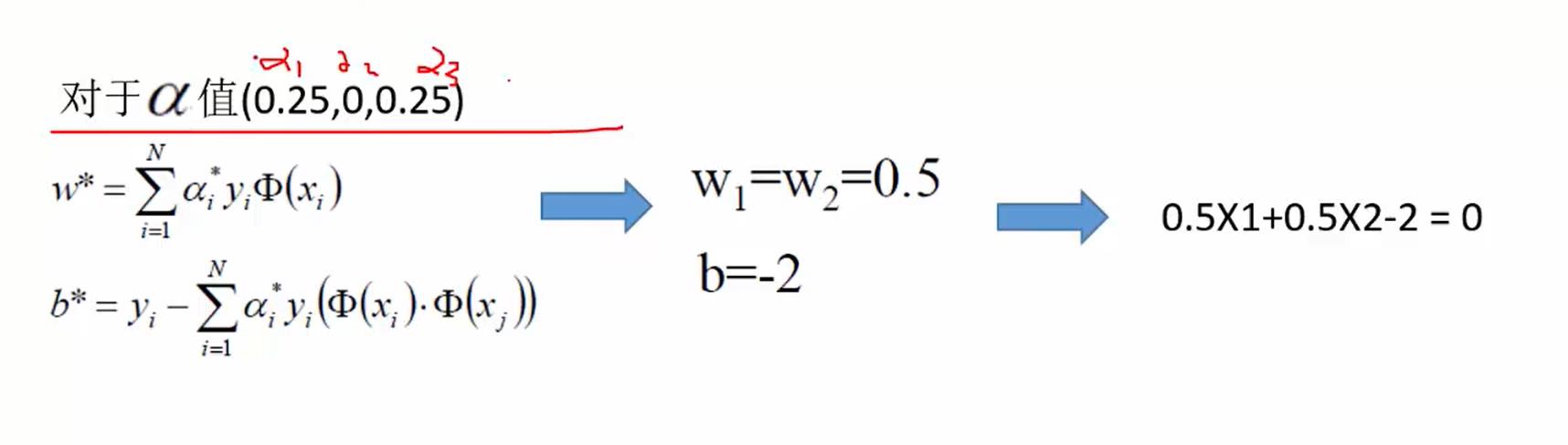
这里的j是指支持向量，也就是α>0的。

软间隔

为什么要有这个玩意，我想应该不用重复了吧，英文版说得我认为还可以。

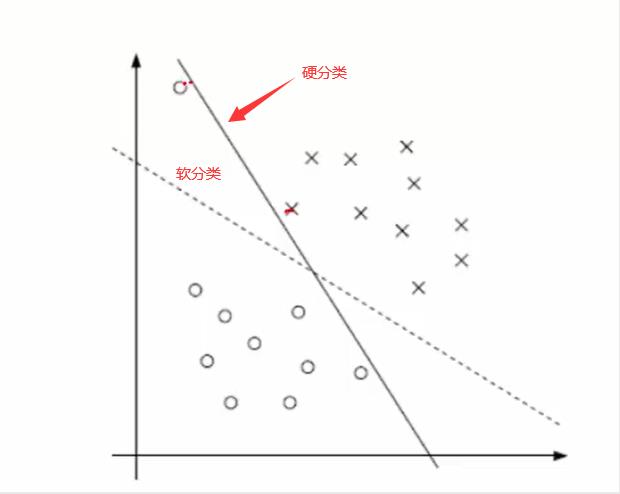
那么在咱们的数学里面就是加一个误差项。

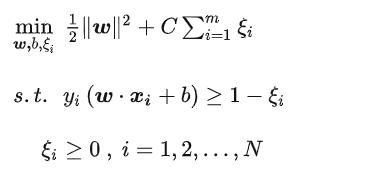
引入一个松弛变量。其实原理就是偏移。

原来是这样的：

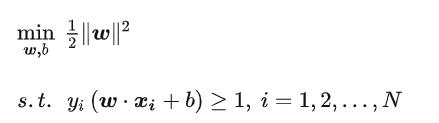
之后得到这样的玩意：

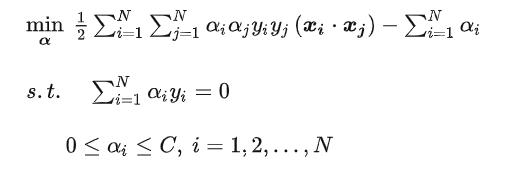
最后：

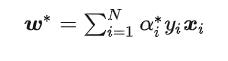
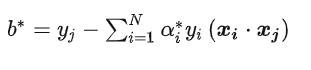
只是多了一个约束

核函数

这个东西咋说呢，在不了解SVM之前，我一直为这玩意很神秘，其实它的本质就是。将一个低纬度的数据映射到一个高维空间，之后在高维空间内划分超平面期望完成分类。

就比如这样的数据：

如果是用直线划分，根本分不出来。

但是如果映射到高纬度空间：

这个就很好划分了，之后在原来二维平面的投影自然就是这样的了：

那么这里也就是需要把x–>f(x)输入刚刚的目标方程就好了。
注：这里涉及到的核函数变化是：

编码

这里先忽略SMO算法，受限于篇幅的问题。你只需要知道这玩意就是一个解方程的启发式算法。

核函数

    def kernelFunction(self,X, A, Ktype):
        """
        :param X:
        :param A:
        :param Ktype: (type,param)
        :return:
        """
        m, n = shape(X)
        K = mat(zeros((m, 1)))
        if Ktype[0] == 'lin':
            K = X * A.T
        elif Ktype[0] == 'rbf':
            for j in range(m):
                deltaRow = X[j, :] - A
                K[j] = deltaRow * deltaRow.T
            K = exp(K / (-1 * Ktype[1] ** 2))
        else:
            raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
        return K

目标函数

这个稍微复杂一点：

    def KKTGoing(self,i):
        """
        Refer to the following 《Statistical Learning Methods》.
        First, check whether ai meets KKT conditions. 
        If not, randomly select aj for optimization 
        and update the values of AI, AJ and B.
        :param self: 
        :return: 
        """
        Ei = self.__calcEk(i)  # 计算E值
        if ((self.labelMat[i] * Ei < -self.tol) and (self.alphas[i] < self.C)) or (
                (self.labelMat[i] * Ei > self.tol) and (self.alphas[i] > 0)): 
            j, Ej = self.__SelectAj(i, self, Ei) 
            alphaIold = self.alphas[i].copy()
            alphaJold = self.alphas[j].copy()
            if (self.labelMat[i] != self.labelMat[j]):
                L = max(0, self.alphas[j] - self.alphas[i])
                H = min(self.C, self.C + self.alphas[j] - self.alphas[i])
            else:
                L = max(0, self.alphas[j] + self.alphas[i] - self.C)
                H = min(self.C, self.alphas[j] + self.alphas[i])
            if L == H:
                print("L==H")
                return 0
            eta = 2.0 * self.K[i, j] - self.K[i, i] - self.K[j, j] 
            if eta >= 0:
                print("eta>=0")
                return 0
            self.alphas[j] -= self.labelMat[j] * (Ei - Ej) / eta  
            self.alphas[j] = self.__HoldAlpha(self.alphas[j], H, L)  
            self.__updateEk(j)
            if (abs(self.alphas[j] - alphaJold) < self.tol): 
                print("j not moving enough")
                return 0
            self.alphas[i] += self.labelMat[j] * self.labelMat[i] * (alphaJold - self.alphas[j]) 
            self.__updateEk(i)  
            
            b1 = self.b - Ei - self.labelMat[i] * (self.alphas[i] - alphaIold) * self.K[i, i] - self.labelMat[j] * (
                        self.alphas[j] - alphaJold) * self.K[i, j]
            b2 = self.b - Ej - self.labelMat[i] * (self.alphas[i] - alphaIold) * self.K[i, j] - self.labelMat[j] * (
                        self.alphas[j] - alphaJold) * self.K[j, j]
            if (0 < self.alphas[i] < self.C):
                self.b = b1
            elif (0 < self.alphas[j] < self.C):
                self.b = b2
            else:
                self.b = (b1 + b2) / 2.0
            return 1
        else:
            return 0

SMO

这个就是解方程：

 def SMO(self,Features, Labels, C, toler, maxIter,Ktype=('lin', 0)):
    	"""
		SMO algorithm is a heuristic algorithm, 
		and I don't know the specific principle. 
		The code comes from Github, 
		and I plan to use PSO algorithm later.
		"""
        self.__SMO_init(mat(Features),mat(Labels).transpose(),C,toler,Ktype)
        iter = 0
        entireSet = True
        alphaPairsChanged = 0
        while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
            alphaPairsChanged = 0
            if entireSet:
                for i in range(self.m):  
                    alphaPairsChanged += self.KKTGoing(i)
                    print("fullSet, iter: %d i:%d, pairs changed %d" % (
                    iter, i, alphaPairsChanged)) 
                iter += 1
            else:
                nonBoundIs = nonzero((self.alphas.A > 0) * (self.alphas.A < C))[0]
                for i in nonBoundIs:  
                    alphaPairsChanged += self.KKTGoing(i)
                    print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
                iter += 1
            if entireSet:
                entireSet = False
            elif (alphaPairsChanged == 0):
                entireSet = True
            print("iteration number: %d" % iter)
        return self.b, self.alphas

其他依赖

训练

 def fit(self,dataSet:DataSet):
        dataArr, labelArr = dataSet.LoadDataSet()
        b, alphas = self.SMO(dataArr, labelArr, 200, 0.0001, 10000, self.Ktype) 
        self.b = b
        self.alphas = alphas
        datMat = mat(dataArr)
        labelMat = mat(labelArr).transpose()
        svInd = nonzero(alphas)[0]
        # Select the number of rows of data that is not 0 (that is, support vector)
        sVs = datMat[svInd]
        labelSV = labelMat[svInd]
        self.sVs = sVs
        self.labelSV = labelSV
        self.svInd  = svInd
        print("there are %d Support Vectors" % shape(sVs)[0])
        m, n = shape(datMat)  
        errorCount = 0
        for i in range(m):
            kernelEval = self.kernelFunction(sVs, datMat[i, :], ('rbf', 1.3))
            predict = kernelEval.T * multiply(labelSV, alphas[
                svInd]) + b
            if sign(predict) != sign(labelArr[i]):  # sign: -1 if x < 0, 0 if x==0, 1 if x > 0
                errorCount += 1
        print("the training error rate is: %f" % (float(errorCount) / m))

模型保存/加载

   def save_model(self,path):
        dict = 
        dict['b'] = self.b
        dict['alphas'] = self.alphas
        dict['sVs'] = self.sVs
        dict['labelSV'] = self.labelSV
        dict['svInd'] = self.svInd
        with open(path,'w') as file:
            file.write(dict)
    def load_mode(self,path):
        if(os.path.exists(path)):
            with open(path) as file:
                model = file.read()
                model = eval(model)
                self.b = model['b']
                self.alphas = model['alphas']
                self.sVs = model['sVs']
                self.labelSV = model['labelSV']
                self.svInd = model['svInd']
        else:
            raise Exception("Fuck you no such file")

评分

 def predict(self,dataSet:DataSet):
        dataArr_test, labelArr_test = dataSet.LoadDataSet() 
        errorCount_test = 0
        datMat_test = mat(dataArr_test)
        m, n = shape(datMat_test)
        for i in range(m):  # 在测试数据上检验错误率
            kernelEval = self.kernelFunction(self.sVs, datMat_test[i, :], ('rbf', 1.3))
            predict = kernelEval.T * multiply(self.labelSV, self.alphas[self.svInd]) + self.b
            if sign(predict) != sign(labelArr_test[i]):
                errorCount_test += 1
        print("the test error rate is: %f" % (float(errorCount_test) / m))

这里的话，API风格尽量和Sklearn看齐，也许你已经猜到我要干啥了。当然实际上我还是要去看看sklearn的具体实现。

完整代码

from numpy import *
import os

class DataSet(object):
    def __init__(self,path):
        self.Features=[]
        self.Labels = []
        self.path = path

    def LoadDataSet(self):
        if(os.path.exists(self.path)):
            with open(self.path) as file:
                for line in file.readlines():
                    lineArr = [float(x) for x in line.strip().split()]
                    self.Features.append([lineArr[0], lineArr[1]])
                    self.Labels.append(lineArr[2])
            return self.Features, self.Labels

        else:
            raise Exception("Fuck you no such file")


class SVMModel(object):

    def __init__(self,Ktype):
        self.Ktype = Ktype

    def __SMO_init(self,Features, Labels, C, toler, Ktype):
        """
        :param Features:
        :param Labels:
        :param C: Soft interval
        :param toler: Stop threshold
        :param Ktype:
        """
        self.X 以上是关于理解SVM模型的目标函数的主要内容，如果未能解决你的问题，请参考以下文章 
 ML-9-4支持向量机--SVM回归模型（SVR）
 SVM算法的另外一种理解
 怎么从通俗意义上理解逻辑回归的损失函数
 SVM预测基于SVM进行股票预测matlab源码
 SVM《软分类与目标函数的推导》
 SVM之KKT条件理解